
Отчет лаба 1
.docxФедеральное агентство по образованию

Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»

Кафедра САПР
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1
«ИССЛЕДОВАНИЕ МЕТОДОВ ОДНОМЕРНОГО ПОИСКА МИНИМУМА УНИМОДАЛЬНЫХ ФУНКЦИЙ»
Выполнил:
Группа:
Проверил:
(Ф.И.О.)
Санкт-Петербург
2012
Оглавление:
Задание…………………………………………………………………………….3
Описание методов оптимизации…………………………………………………3
Блок-схема программы………………………………………………………..…5
Спецификация программы……………………………………………………….6
Текст программы ………………………………………………………………....6
Результаты тестирования…………………….………….……………………….8
Графическая интерполяция………………………………………………………8
Выводы…………………………………………………………………………….9
Ответы на контрольные вопросы………………………………………………...9
Задание:
Изучение методов одномерной минимизации функций одной переменной, разработка программы.
Описание методов оптимизации:
Метод Свенна:
С помощью этого метода получаем начальный интервал локализации минимума.
Начальный этап:
1) задать x0 – произвольная начальная точка.
2) выбрать шаг h равным 0.001 или 0.01*|x0|.
Основной этап:
Шаг 1:
Установить направление убывания целевой функции. Для этого надо взять x2=x1+h. Если f1<f2, то надо поменять направление движения(h=-h и взять x2=x1+h).
Шаг 2:
Вычислять fk в точках xk+1=xk+hk, где hk=2hk-1, k=2,3,…,n-1 до тех пор пока не придём в точку xn такую что fn>fn-1.
Шаг 3:
Установить начальный интервал локализации минимума a1=xn-2 и b1=xn.
Метод дихотомии:
Начальный этап:
-
Предположить, что функция унимодальная.
-
Есть известная начальная точка x1.
-
Получить интервал методом Свенна
Основной этап:
Шаг 1:
Взять 2 точки k и k на расстоянии /2 от центра текущего интервала. Сокращаем ТИЛ, если f1<f2 то возвращаемся в начало шага.
Шаг 2:
Проверка критерия окончания поиска.
Наращиваем счетчик числа операций k=k+1, пока (bk – ak) ≤ ε, если условие не выполняется, то возвращаемся на шаг 1.
Метод Ньютона:
Начальный этап:
1) Ввести начальное приближение x0 и условие остановки .
2) Принять k = 0.
Основной этап:
Шаг 1:
Определить направление спуска pk.
Шаг 2:
Определить последующую точку xk+1=xk+pk.
Шаг 3:
Вычислить в точке xk+1 градиент.
Шаг 4:
Если ||f '(xk+1)|| ε, то поиск на этом заканчивается и полагается
x = xk+1 и y = f(xk+1).
Иначе k = k + 1 и переход к шагу 1.
x,x1,x2, h=0.01,e=0.001 Начало f(x2)> f(x1) h=-h; x2=x1+h;
Да




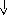

Нет



h=Sven
(x1,x2,h);


cout<<a cout<<b
x1=a; x2=b; x1=x2-dif(x2)/dif2(x2); k++; while
(fabs(x1-x2)>e && fabs(dif(x1))>e); cout<<x1 Конец





Спецификация программы:
a, b – текущий интервала локализации
h – размер шага
min –минимум
x1 – стартовая точка
k, k1 – счетчики числа итераций.
Текст программы:
#include <conio.h>
#include <math.h>
#include <iostream.h>
long double a,b;
int k1, k;
double fx(double x) // функции
{
// возрат в зависимocти от x
if(x>=0)
return (4*x*x*x-3*x*x*x*x);
else
return (4*x*x*x+3*x*x*x*x);
}
double dif(double x) // производные для ньютона
{ if(x>=0)
return (12*x*x-12*x*x*x);
else
return (12*x*x+12*x*x*x);
}
double dif2(double x)
{ if(x>=0) return (24*x-36*x*x);
else return (24*x+36*x*x);
}
double Sven(long double x1, long double x2, long double h)
{ // Метод Свенн
long double x3,z;
x2=x1+h;
while (1)
{
h=2*h;
x3=x2+h;
if (fx(x3)>fx(x2))
break;
x1=x2;
x2=x3;
k1=k1+1;
}
a=x1;
b=x3;
if (a>b) // a – всегда слева, b - справа
{
z=b;
b=a;
a=z;
}
return h;
}
void main()
{
clrscr();
double x1,x2,h=0.01,e=0.001;
x1=0.4; //Начальня точка
x2=x1+h;
cout<<"\nNach tochka x1: "<<x1;
if ( fx(x2) > fx(x1))
{
h=-h; // меняем знак если функция растет
x2=x1+h;
}
h=Sven (x1,x2,h);
cout << "\n\nsSchag svenn. k= " << k1;
cout << "\nInterval posle Svenn";
cout << "\na= " << a << endl;
cout << "b= " << b << endl;
do // Ньютон
{
x1=a;
x2=b;
x1=x2-dif(x2)/dif2(x2);
k++;
cout<<"\nx1-x2;
}
while(fabs(x1-x2)>e && fabs(dif(x1))>e);
cout << "\n\nsSchag Nuton. k= " << k;
cout << "\n\nMinimum= " << x1;
getch();
}
Результаты работы программы
интервал по Свенну: -2.15 … -0.23
число повторений цикла после установления интервала k=6
минимум функций по Ньютону 1.000000
График функции

Выводы:
В результате лабораторной работы были изучены методы одномерной минимизации функций одной переменной. Минимум функции был найден посредством метода Свенна и последующего применения метода Ньютона (результат совпал с ожидаемым).
Ответы на контрольные вопросы:
1. Сравните метод золотого сечения, Фибоначчи и дихотомического поиска по числу вычислений значений функций для достижения заданной точности при локализации минимума.
Метод дихотомии наиболее прост в реализации, но по сравнению с методом золотого сечения он менее эффективен. Метод Фибоначчи использует числа Фибоначчи и поэтому он быстрее сходится к искомому минимуму, чем метод золотого сечения. 2.Указать отличие метода золотого сечения 1 от метода золотого сечения 2?
ЗС-1 опирается на точное вычисление точек на каждой итерации, а ЗС-2 использует соблюдения правила симметрии и для старта требуется указать одну и только одну точку.
3. Как сокращается текущий интервал локализации минимума в методах Фибоначчи-1 и Фибоначчи-2? Фиб1: Начальный этап
(1) Задать константу , начальный интервал [a1, b1], длину конечного интервала Ln и определить число n так, чтобы выполнялось условие Fn > (b1 - a1)/Ln.
(2) Взять две пробные точки 1 = a1 + (Fn-2/Fn)(b1 - a1) и 1 = a1 + (Fn-1/Fn)(b1-a1). Положить k = 1.
Основной этап
Шаг 1. Сократить текущий интервал локализации:
(1) Если f(k) < f(k), то положить ak+1 = ak, bk+1 = k,k+1 =k и вычислить новую точку k+1 = ak+1 + (Fn-k-2/Fn-k)Lk+1, где Lk+1 = bk+1 - ak+1; перейти на шаг 2.
(2) Если f(k)>> f(k),то положить ak+1 =k, bk+1 = bk, k+1 = k и вычислить k+1 = ak+1 + (Fn-k-1/Fn-k) Lk+1.
Шаг 2. Проверить критерий окончания поиска:
(1) Заменить k на k+1. (2) Если k = n - 1, перейти на шаг 3, иначе - на шаг 1.
Шаг 3. Найти аппроксимирующий минимум х(*):
(1) Положить k = k + .
(2) Если f(k) > f(k), то x(*) = (k + bk)/2. В противном случае - x(*) = (ak + k)/2.
Фиб2 : сокращение происходит аналогично, только вначале берется не 2 точки а одна, которая откладывается от любого из концов интервала, и все последующие точки берутся по правилу симметрии Х2 = Ак+Вк–Х1 и сравнением 4ех ситуаций (как в методе ЗС-2) происходит сокращение интервала.
4. Определите достоинства и недостатки методов Ньютона и трехточечного поиска.
Метод трехточечного поиска позволяет сократить интервал локализации минимума на основе сравнения значений функции в пробных точках без вычисления производных. А в методе Ньютона минимизация f(x) основывается на использовании квадратичной аппроксимации функции f(x) в точке xk:
F(x) = f(xk) + f '(xk)(x - xk) + f ''(xk)(x - xk)2 * 1/2
В качестве приближения хk+1 к минимуму х* берется точка, в которой производная F'(x) равна нулю, т.е. f '(xk) + f ''(xk)(xk+1 -xk) = 0.
Таким образом, xk+1 = xk - f '(xk)/f ''(xk).
Итерационный процесс строит последовательность точек {xk}, которая при определенных условиях квадратично сходится к некоторой стационарной точке х* функции f(x), т.е. к точке, в которой f ' (x*) = 0. Процесс останавливается, когдаxk+1 - xk ≤ и f '(xk) ≤ , где > 0 - заранее заданное малое число.
Существенными недостатками метода Ньютона являются: 1) сложность задания начального приближения х1 в малой окрестности искомого минимума х*; 2) необходимость вычисления вторых производных минимизируемой функции.
5.Что такое унимодальная функция и каково её значение в теории оптимизации?
Унимодальная функция – это функция которая имеет единственный минимум и монотонна по обе стороны от него. При этом у неё не должно быть горизонтальных участков. Унимодальная функция является основой в теории поиска, так как она разработана для большинства методов поиска.
6.Сформулировать необходимые и достаточные условия минимума функции одной переменной? Как преобразовать задачу на поиск максимума в задачу на минимум?
Аналитическое условие экстремума, т.е. равенство производной функции в данной точке, является необходимым и достаточным условием минимума. Задача на поиск максимума преобразуется в задачу на поиск минимума противоположной функции, т.е. задача на поиск максимум функции F(x), а на поиск минимума (-F(x))
7.Характерные особенности организации одномерного поиска?
Линейный поиск, рассматриваются только унимодальные функции.
Начальный интервал локализации минимума находится методом Свенна
Меньший интервал локализации получается путём рассмотрения значений функции в двух точках на ТИЛ, или в производной в одной точке, и выборе новых границ интервала.
8. Дайте геометрическую интерпретацию 2-х способов выбора последних точек в методе Фибоначчи.
Точки в методе Фибоначчи 1 находятся по формулам:
k+1 = ak+1 + (Fn-k-2/Fn-k)Lk+1 и k+1 = ak+1 + (Fn-k-1/Fn-k) Lk+1.
А очередная точка в методе Фибоначчи 2 находится по правилу симметрии Х2 = Ак+Вк–Х1
