Федеральное агентство по образованию

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

Кафедра САПР

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 3

«Исследование методов линейного поиска»

Выполнил: .

Группа:

Проверил:

(Ф.И.О.)

Санкт-Петербург

2012

Оглавление:

Задание…………………………………………………………………………….3

Описание методов оптимизации…………………………………………………3

Блок-схема программы………………………………………………………..…5

Спецификация программы……………………………………………………….6

Текст программы ………………………………………………………………....6

Результаты работы программы……...……….………….……………………….9

Выводы…………………………………………………………………………….9

Ответы на контрольные вопросы………………………………………………...9

Задание:

Разработка программы, реализующей комбинированную процедуру минимизации функции многих переменных в заданном направлении.

Описание методов оптимизации.

Метод Свенна:

С помощью этого метода получаем начальный интервал локализации минимума.

Начальный этап:

1) задать x⁰ – произвольная начальная точка.

2) выбрать шаг h равным 0.001 или 0.01*|x⁰|.

Основной этап:

Шаг 1:

Установить направление убывания целевой функции. Для этого надо взять x₂=x₁+h. Если f1<f2, то надо поменять направление движения(h=-h и взять x₂=x₁+h).

Шаг 2:

Вычислять f_k в точках x_k+1=x_k+h_k, где h_k=2h_k-1, k=2,3,…,n-1 до тех пор пока не придём в точку x_n такую что f_n>f_n-1.

Шаг 3:

Установить начальный интервал локализации минимума a₁=x_n-2 и b₁=x_n.

Метод Фибоначчи:

Начальный этап.

1. задать начальный интервал [a₁,b₁], длину конечного интервала L_n и определить число n так, чтобы выполнялось условие F_n>(b₁-a₁)/L_n.

2. Взять 2 точки _k=a₁+(F_n-2/F_n)(b₁-a₁) и _k=a₁+(F_n-1/F_n)(b₁-a₁)_.

Основной этап

Шаг 1:

Сократить текущий интервал локализации:

Если f(_k)<f(_k), то a_k+1=a_k, b_k+1=_k, _k+1=_k и вычислить новую точку, перейти к шагу 2. Если f(_k)≥f(_k), то a_k+1=_k , b_k+1= b_k, _k+1=_k и вычислить _k+1.

Шаг 2:

Проверить критерий окончания поиска:

1. Заменит k на k+1

2. Если k=n-1, перейти к шагу 3, иначе к шагу 1

Шаг 3:

Найти аппроксимирующий минимум x^(*).

1. _k=_k+ε

2. Если f(_k)>f(_k), то x^(*)=(_k+ b_k)/2, иначе x^(*)=(a_k+ _k)/2

Метод Давидона:

Начальный этап

1. Выбрать ε, x⁰, p, α₁

2. Методом Свенна получить интервал [a, b].

Основной этап

Шаг1:

Найти аппроксимирующий минимум, т.е. точку d по формулам:

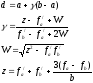
Шаг2

Проверка критерия окончания поиска:

1. Если y`<sub>r</sub>≤ ε, то остановиться, х=a+α<sub>r</sub>p. Иначе: сократить ТИЛ: если y`_r <0, то [r,b], если y`_r >0, то [a,r].

2. Положить k=k+1 и вернуться на шаг 1.

Начало

k=0, x10=0, x20=3, p1=1, p2=0

Sven (p1,p2);

cout<<a1

cout<<b1

Fibbonachi(a1,b1,b,L)

cout<<a

cout<<b

Конец

Davidon(a,b)

cout<<x1

cout<<x2

Спецификация

a, b – текущий интервала локализации

x10, x20 – начальная точка

p1, p2 – направление поиска

x* - значение минимума

k – счетчики числа итераций.

Текст программы:

#include<conio.h>

#include<iostream.h>

#include<iomanip.h>

#include<math.h>

double a, b, x1, x2, x10, x20, r1, p1, p2, n, F, L, Ln, alpha, e=0.01;

int k;

double fc(double alpha)

{ return(pow((x10+alpha*p1-2),4)+pow((x10+alpha*p1-2*(x20+alpha*p2)),2));

}

double pr(double a)

{

double g1, g2;

g1=4*pow(((x10+a*p1)-2),3)+2*((x10+a*p1)-2*(x20+a*p2));

g2=-4*((x10+a*p1)-2*(x20+a*p2));

return (g1*p1+g2*p2);

}

double Svenn(double p1, double p2)

{

alpha=0.1;

k=0;

if(pr(alpha) < 0)

{ p1=+p1;

p2=+p2;

}

else

{ p1=-p1;

p2=-p2;

}

do

{

k=k+1;

alpha=2*alpha;

}

while(pr(alpha)<0);

return alpha;

}

double fib (double s)

{ double fib1=1; double fib2=1;

double sum;

for(int y=2;y<s;y++)

{ sum=fib1+fib2;

fib1=fib2;

fib2=sum;

}

return sum;

}

double Fibbonachi(double a1, double b1, double n, double L)

{

x1=a1+(fib(n-2)/fib(n))*L;

x2=a1+(fib(n-1)/fib(n))*L;

k=0;

for(int i=0; i<n; i++)

{

if(fc(x1)>=fc(x2))

{ a1=x1;

b1=b1;

x1=x2;

L=fabs(b1-a1);

x2= a1+b1-x1; //a1+(fib(n-i-2)/fib(n))*L;

}

else

{ a1=a1;

b1=x2;

x2=x1;

L=fabs(b1-a1);

x1=a1+b1-x2; //a1+(fib(n-i-3)/fib(n))*L;

}

k=k+1;

}

if(fc(x1)>=fc(x2))

alpha=(x1+b1)/2;

else

alpha=(x2+a1)/2;

return alpha;

}

double Davidon(double a, double b)

{

double alpha_min, w, z, e, q1,q2,q3;

e=0.001;

int y=0;

do

{

z=pr(a)+pr(b)+(3*(fc(a)-fc(b)))/(b-a);

q1=(pr(a));

q2=(pr(b));

q3=(z*z);

w=sqrt(q3-q2*q1);

r1=a+(b-a)*((w-pr(a)+z)/(2*w-pr(a)+pr(b)));

if(pr(r1) > 0)

{

b=r1;

}

else

{

a=r1;

}

++y;

}

while(fabs(pr(r1))>=e);

return r1;

}

void main()

{

clrscr();

k=0;

x10=0;

x20=3;

p1=1;

p2=0;

Svenn (p1, p2);

cout<<"Posle Svenn"<<endl;

// x1=x10+alpha/4*p1;

// x2=x20+alpha/4*p2;

// cout<<"\na= "<<x1<<", b= "<<x2<<"]";

x1=x10+alpha*p1;

x2=x20+alpha*p2;

double a1=alpha/4;

double b1=alpha;

cout<<"a1="<<a1<<" b1="<<b1<<endl<<endl;

Ln=0.2;

L = fabs(b1-a1);

F = L/Ln;

n = log(F*sqrt(5))/log(1.618);

Fibbonachi(a1,b1,b,L);

cout<<"Posle Fibonachi"<<endl;

a=x10+alpha*p1;

b=x20+alpha*p2;

cout<<"a= "<<a<<" b= "<<b<<endl<<endl;

Davidon(a,b);

x1=x10+r1*p1;

x2=x20+alpha*p2;

cout<<"Posle Davidona"<<endl;

cout<<"x1= "<<x1<<" x2= "<<x2<<endl;

getch();

}

Результаты работы программы:

Интервал по Свенну: a= -0,8 b=3

Число повторений цикла после установления интервала k=5

Метод Фибоначчи: а = 3,2 b=3

Метод Дэвидона: х1= 3,12818 x2= 3

Выводы:

В данной работе сравниваются 2 метода линейный и аппроксимационный для функции двух переменных. Как показали результаты метод Дэвидона очень эффективен и он выполняет задачу за одну интерацию.

Ответы на контрольные вопросы:

1. Пояснить организацию линейного поиска на основе методов золотого сечения, Фибоначчи и Пауэлла.

Поиск минимума по направлению производится с использованием одномерных методов, т.е. сначала многомерная функция сводится к одномерной функции зависящей от смещения по заданному направлению из заданной точки, а потом для неё вызывается один из методов одномерной минимизации

2. Аналитически найти производную в точке x¹ = (1; 0)^t по направлению p¹ = (1; 1)^t для функции y(x) = x₁² – x₁x₂ + 2x₂² – 2x₁

y’_x1 = 2 x₁ - x₂ – 2; y’_x2 = - x₁ + 4 x₂;

grad (x¹) = [ 0 ; -1];

y’ = 0*1 + (-1)*1 = -1;

3. Как изменится процедура минимизации методами Больцано, дихотомии, ДСК, Дэвидона при переходе от поиска на числовой прямой к поиску на плоскости R²?

F(x) -> F(x₁,x₂)

Числа a,b,λ,µ -> векторы a,b, λ,µ или смещения относительно начальной точки α _b α_a … КОП: |b-a|<ε -> ||a-b||<ε модуль заменится нормой

Y’(r) -> Y’(r,p) производная станет по направлению.

x_k+1=x_k+h_k, h_k=2h_k-1 -> x_k+1=x_k+h_k*p, h_k=2h_k-1 шаг на h станет шагом на h в направлении p.

5. Что является направлением наискорейшего спуска в точке x¹ = (1; 1)^t для целевой функции y(x) = x₁² + 2x₂²?

Им является вектор антиградиент в точке x = (1,1)^t G= (2*x₁,4*x₂)^t B точке х G= (2,4) ^t антиградиент -G= (-2,-4) ^t

6. Найти минимум y(x) = x₁² – x₁x₂ + 2x₂² – 2x₁ + e^x1 + x2, двигаясь из точки x¹ = (0; 0)^t в направлении наискорейшего спуска.

Градиент G(x)= (2x₁-x₂-2+e^x1+x2,4x₂-x₁+e^x1+x2)^t G(x₀)= (-1,1)^t антиградиент -G= (1,-1)^t

Y’(x,p) = (2x₁-x₂-2+e^x1+x2,4x₂-x₁+e^x1+x2)* (1,-1)^t = 3x₁ -5x₂-2=0

-3x₁+5x₂+2=0

x₁= α

x₂= - α

3 α+5 α-2=0

8 α-2=0

α= 0.25

x₁= 0.25

x₂= -0.25

X=(0.25, -0.25)^t