1.3. Основные механические характеристики жидкости

К основным механическим характеристикам жидкости относят плотность и удельный вес.

Плотность ρ – это отношение массы жидкости m к её объёму W:

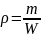. (1.3)

Единицей измерения плотности ρ в системе СИ является кг/м³.

Удельный вес γ (Н/м³) – это отношение веса жидкости к её объёму:

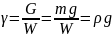. (1.4)

Плотность жидкостей и газов зависит от температуры и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности с увеличением температуры. Плотность воды максимальна при t = 4 ºС и уменьшается как с уменьшением, так и с увеличением температуры от этого значения. В этом проявляется одно из аномальных свойств воды.

Плотность дистиллированной воды при t = 4º С составляет 1000 кг/м³; морской воды - 1020 … 1030 кг/м³; воды из Мёртвого озера (Израиль) - 1300…1400 кг/м³; нефти и нефтепродуктов – 650 … 900 кг/м³; чистой ртути – 13600 кг/м³. Величины плотности газов меньше плотности жидкости примерно на три порядка. Например, плотность воздуха при атмосферном давлении и температуре t = 0 ºС составляет ρ_в = 1,293 кг/м³.

Плотность жидкости можно определить непосредственным взвешиванием, или с помощью ареометра, который действует на основе закона Архимеда. Существуют также различные автоматические анализаторы плотности жидкости. Плотность газов определяют с помощью различных плотномеров (ареометрические, вибрационные, акустические и т. д.), или косвенным методом (измерением параметров состояния среды, определения её состава и проведения соответствующих расчётов).

1.4. Основные физические свойства жидкостей и газов

Сжимаемость. При изменении давления в жидкости изменяется её объём, следовательно, изменяется и плотность. Это свойство называется сжимаемостью жидкости, которое характеризуется коэффициентом объёмного сжатия β_р, 1/Па, представляющим собой относительное изменение объёма жидкости при изменении давления на единицу:

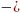
β_р = 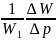= 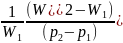, (1.5)

где W₁ – первоначальный объём жидкости;

W₂ – конечный объём жидкости;

∆W– изменение объёма жидкости при изменении давления на величину ∆р.

Знак ″–″ в формуле (1.5) указывает на то, что при увеличении давления объём жидкости уменьшается (W₂ < W₁).

Поскольку сжимаемость жидкости очень незначительна, то в большинстве случаев при инженерных расчетах сжимаемостью пренебрегают. Однако при эксплуатации гидравлических систем возможны ситуации, когда давление в жидкости значительно увеличивается (например, вследствие резкого закрытия или открытия запорного устройства в трубопроводе). В таких случаях сжимаемость жидкости нужно учитывать. Если бы вода в Мировом океане (средняя глубина 3700 м) была несжимаемой, её уровень повысился бы на 27 м. Объём лёгкого минерального масла, применяемого в жидкостных амортизаторах шасси самолётов при нормальной температуре, уменьшается при повышении давления от 0 до 35 МПа на 1,7 %, а керосина – на 0,8 %.

После снятия внешней нагрузки ∆р на жидкость её первоначальный объём восстановится. Это свойство характеризует упругие свойства жидкости. Выражение (1.5) по существу, представляет собой известный закон Гука для модели объёмного сжатия. В качестве меры упругого сжатия жидкости принимают величину, обратную коэффициенту объёмного сжатия – модуль объёмной упругости жидкости Е₀, Па:

Е₀ = 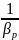. (1.6)

Физический смысл объёмного модуля упругости можно представить, если считать, что первоначальный объём W₁ = 1 м³, изменение давления ∆р = 1 Па. Тогда согласно (1.5) и (1.6) выражение для Е₀ будет равно:

Е₀ = ,

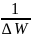то есть модуль упругости можно представить как величину, обратную изменению одного кубического метра жидкости при изменении давления на одну единицу.

Различают изотермический и адиабатный модуль упругости. Обычно при расчетах используют изотермический модуль упругости Е_0т, применяемый при анализе медленных процессов, при которых успевает завершиться теплообмен с окружающей средой. Адиабатный модуль упругости несколько больше изотермического и используется при быстротечных процессах, например, при гидравлическом ударе в трубах. Модуль упругости зависит от температуры и давления, и обычно при расчётах гидравлических систем используют среднее значение изотермического модуля упругости (средние значения Е_0т для некоторых жидкостей приведены в табл. 1).

Таблица 1

Значения изотермического модуля упругости Е_0т для некоторых жидкостей

Жидкость	Изотермический модуль упругости Е0т, МПа	Жидкость	Изотермический модуль упругости Е0т, МПа
Ртуть	32373	Вода	2060
Глицерин	4464	Керосин	1275
Глинистые растворы	2500	Силиконовая жидкость	1030

Плотность жидкости при увеличении давления изменяется незначительно, и обычно это изменение не учитывают. Например, при увеличении давления с 0,1 МПа до 10 МПа (в 100 раз) плотность воды увеличится на 0,5 %. Таким образом можно считать, что плотность жидкости практически не зависит от давления.

Как уже отмечалось ранее, сжимаемость газов очень значительна, и её необходимо учитывать при расчёте газовых систем. Закон, связывающий между собой давление и объём газа, носит название закона Бойля – Мариотта (сначала этот закон был открыт Р. Бойлем в 1662 году, а затем независимо от Бойля еще раз Э. Мариоттом в 1679 году): при постоянной температуре и массе идеального газа произведение его давления р и объёма W постоянно:

р₁W₁ = р₂W₂ = const .

Например, если некоторое количество газа сжимается до половины своего объёма, то давление в газе увеличивается в два раза, и наоборот. Этот закон, как было отмечено в формулировке, справедлив для идеальных газов. Идеальный газ – это математическая модель газа, которая предполагает, что молекулы газа обладают лишь кинетической энергией. При этом силы притяжения или отталкивания между молекулами отсутствуют, время взаимодействия между молекулами пренебрежительно мало, соударения частиц между собой и со стенками сосуда абсолютно упруги.

Однако при сжатии газа выделяется теплота, и если газу не будет предоставлено время для выравнивания разности температур (будет происходить адиабатный процесс), то очевидно, что увеличение давления будет происходить в бόльшем отношении, чем уменьшение объёма. В этом случае закон Бойля – Мариотта имеет вид:

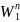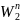р₁ = p₂ , (1.7)

где n – степенной показатель, равный отношению удельной теплоёмкости при постоянном давлении к удельной теплоёмкости при постоянном объёме (для сухого атмосферного воздуха n = 1,405).

При изотермическом процессе n = 1. На практике обычно процесс изменения состояния газа происходит между двумя границами (изотермический и адиабатный процессы) и называется политропным. Степенной показатель n (показатель политропы) для сухого атмосферного воздуха изменяется в пределах 1 < n < 1,405. Процесс изменения состояния газа в трубопроводах систем газоснабжения с достаточной точностью можно считать изотермическим.

Температурное расширение. Это свойство жидкостей изменять свой объём при изменении температуры; характеризуется температурным коэффициентом объёмного расширения β_t (1/ ºС), представляющим собой изменение объёма жидкости при изменении температуры на одну единицу (1 ºС) при постоянном давлении:

β_t = 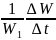= 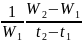, (1.8)

где W₁ – первоначальный объём жидкости;

W₂ – конечный объём жидкости;

∆W – изменение объёма жидкости при изменении температуры на ∆t.

Иными словами, β_t – это число, выражающее относительное увеличение объёма жидкости при увеличении температуры на 1/ ºС. Для воды при разных давлениях и температуре коэффициент β_t изменяется в пределах: β_t ≈ 0,00014 … 0,00066 (1/ ºС). Изменение объёма жидкости при увеличении температуры незначительно, и обычно учитывается при значительных перепадах температуры. Для большинства жидкостей коэффициент объёмного расширения β_t с увеличением давления уменьшается.

Изменение плотности жидкости при изменении температуры определим, исходя из логического предположения, что масса m жидкости при изменении температуры не изменяется, изменяются её объём и плотность:

m = ρ₀ ∙W₁ = ρ_t ∙ (W₁ + ∆W), (1.9)

где ρ₀ – плотность при начальной температуре t₁;

ρ_t – плотность при температуре t₂ = t₁ + ∆t (∆t – изменение температуры).

Выразим из уравнения (1.9) плотность ρ_t , а из (1.8) – изменение объёма ∆W:

∆W = β_t ∙W₁∙∆t; ρ_t = ;

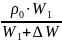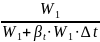ρ_t = ρ₀ = ρ₀ .

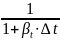Поскольку плотность жидкости незначительно, но зависит от давления, то в последнем выражении при определении ρ_t её значение можно установить лишь приближённо:

ρ_t ≈ ρ₀ 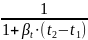. (1.10)

Зависимость плотности жидкости от температуры широко используется для создания естественной циркуляции в отопительных системах, для удаления продуктов сгорания и т.д.

Зависимость объёма газа от температуры математически выражается уравнением, которое называют законом Гей – Люссака (закон был впервые опубликован в 1802 году):

W = W₀(1 + κt), (1.11)

где W₀ – объём газа при 0 ºС;

t – действительная температура;

κ – коэффициент расширения, равный увеличению объёма газа на 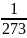того объёма, который этот газ занимал при 0 ºС при увеличении температуры на 1 ºС (κ = ).

Закон Гей – Люссака справедлив при условии, что давление газа при изменении температуры остаётся неизменным. Следует, однако, иметь ввиду, что этот закон не оправды­вается, когда газ сильно сжат или настолько охлажден, что он приближается к состоянию сжижения. В этом случае пользоваться формулой (1.11) нельзя.

Вязкость. Это свойство жидкости оказывать сопротивление действию внешних сил, вызывающих перемещение её частиц или слоёв.

Вязкость проявляется в том, что при относительном перемещении слоёв жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения или силами вязкости. Благодаря этим силам слой жидкости, движущийся медленнее, «тормозит» соседний слой, движущийся быстрее. Силы внутреннего трения проявляются вследствие наличия межмолекулярных связей между движущимися слоями и хаотическим тепловым движением молекул.

Силы внутреннего трения в жидкости впервые были обнаружены Ньютоном в 1686 г., а затем экспериментально обоснованы проф. Н. П. Петровым в 1883 г. Для выяснения физической сущности понятия вязкости рассмотрим следующую схему (рис. 1.2).

Рис. 1.2. Схема к определению вязкости жидкости

Выделим в движущейся жидкости два соседних слоя, один из которых движется со скоростью u₁, а другой - со скоростью u₂. Молекулы жидкости этих слоёв могут иметь как направленное движение, совпадающее с направлением движения потока жидкости (молекулы А и В), так и хаотическое движение со своей собственной скоростью (молекулы С и D). Между молекулами А и В действуют силы взаимного притяжения, и молекула А, движущаяся медленнее, будет «тормозить» движение молекулы В. В то же время молекула С, попадая в верхний слой, будет тормозить его движение. Очевидно, что между слоями появятся силы внутреннего трения, направленные против движения жидкости по отношению к верхнему слою.

Рис. 1.3. Профиль скорости в потоке вязкой жидкости

Силы внутреннего трения возможны только в движущейся жидкости, то есть вязкость жидкости проявляется лишь при её течении. Движение слоёв жидкости с разными скоростями возникает при её движении вдоль твёрдых поверхностей, так как скорость движения жидкости у твёрдой поверхности равна нулю. Частицы жидкости как бы «прилипают» к поверхности, сцепляясь с ней. Поэтому скорость движения жидкости увеличивается от нуля у твёрдой поверхности до скорости основной массы жидкости (рис. 1.3).

Ньютоном было высказано предположение, впоследствии подтверждённое опытом, что силы внутреннего трения F_тр пропорциональны площади соприкосновения слоёв S и относительной скорости перемещения слоёв du (скорости скольжения):

F_тр = μ S ,

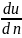где du/dn – градиент скорости (скорость деформации сдвига), то есть величина изменения скорости в направлении, нормальном к направлению вектора самой скорости;

μ – коэффициент пропорциональности, учитывающий особенности конкретных жидкостей и называемый коэффициентом динамической вязкости жидкости (или просто динамической вязкостью жидкости).

Если отнести силу трения F_тр к единице поверхности, то получим не что иное, как касательное напряжение τ:

τ = μ . (1.12)

В память французского учёного Пуазейля единица динамической вязкости была названа «пуаз»: 1П = 1 г/(см·с) в системе СГС. В системе СИ единицей динамической вязкости является 1 Па·с = 1 кг/(м·с); 1 Па·с = 10 П.

В гидравлических расчётах кроме динамической вязкости наиболее часто используют понятие кинематической вязкости, равное отношению динамической вязкости μ к плотности жидкости ρ:

ν = 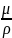. (1.13)

Название «кинематическая вязкость» отражает тот факт, что в размерность входят только кинематические (а не динамические) величины. Единицей кинематической вязкости в системе СИ является м²/с. В системе СГС принята единица см²/с, названная в честь английского учёного Стокса «стокс»; 1 м²/с = 10⁴ Ст. Сотая доля стокса называется сантистоксом (сСт).

Жидкости, для которых справедлив закон внутреннего трения Ньютона (1.12), называются ньютоновскими.

Существуют жидкости (коллоидные суспензии, растворы полимеров, гидросмеси из глины, цемента, строительные растворы, донные осадки сточных вод, сапропели, краски и т.п.), для которых связь между касательным напряжением τ и скоростью деформации сдвига du/dn будет выражаться соотношением:

τ = τ₀ + μ 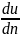. (1.14)

Такие жидкости относятся к неньютоновским и называются вязкопластичными, аномальными или бингамовскими. Опытами установлено, что в подобных жидкостях движение наступает только после того, как за счёт внешних сил, действующих на жидкость, будет преодолено некоторое значение касательного напряжения, обычно называемого начальным напряжением сдвига τ₀. Таким образом, вязкопластичные жидкости отличаются от ньютоновских наличием касательного напряжения в состоянии покоя τ₀.

Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней. При увеличении температуры капельной жидкости коэффициенты её вязкости (как динамиче­ский, так и кинематический) резко снижаются в десятки и сотни раз, что обусловлено уве­личением внутренней энергии молекул жидкости по сравнению с энергией межмолеку­лярных связей в жидкости. Вязкость жидкостей зависит также и от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей возрастает. Исключением является вода, для которой при температуре до 32 ºС с увеличением давления вязкость уменьшается.

В отличие от капельных жидкостей, вязкость газов увеличивается при увеличении температуры, так как с увеличением температуры газа возрастает скорость теплового движения молекул, что делает газ более вязким. Зависимость вязкости газа от давления ничем не отличается от аналогичной зависимости для капельных жидкостей.

Изучению методов измерения вязкости посвящён целый раздел физики - вискозиметрия. Вязкость жидкостей измеряют при помощи вискозиметров. Существующее разнообразие методов измерения вязкости и конструкций вискозиметров обусловлено как широким диапазоном значений вязкости (от 10^-5 Па∙с для газов до 10¹² Па∙с для ряда полимеров), так и необходимостью измерения вязкости в условиях низких или высоких температур и давлений (например, сжиженных газов, расплавленных металлов, водяного пара при высоких давлениях и т. д.). Наиболее распространены три метода измерения вязкости жидкостей и газов: капиллярный, ротационный, и метод падающего шара.

В капиллярном вискозиметре вязкость определяют по времени истечения заданного объёма жидкости через калиброванное отверстие (капилляр). Как правило, определяют кинематическую вязкость. Предварительно вязкость определяют в секундах истечения, а затем рассчитывают по формуле ν = κt, где κ – постоянная вискозиметра, приведённая в паспорте, мм²/с²; t - среднее арифметическое время истечения, сек. В различных странах для определения вязкости используют вискозиметры Энглера (в Европе), Сейболта (в США), Редвуда (в Великобритании). При использовании вискозиметра Энглера вязкость определяют в градусах Энглера °Е (отношение времени истечения испытуемой жидкости объёмом 200 см³ ко времени истечения воды того же объёма при температуре 20 °С), а затем вычисляют по соответствующей формуле.

В ротационных вискозиметрах определяют динамическую вязкость по крутящему моменту с установленной скоростью ротора или по скорости вращения ротора при заданном крутящем моменте (например, вискозиметр Брукфильда). Ротационный метод вискозиметрии заключается в том, что исследуемая жидкость помещается в малый зазор между двумя телами, который необходим для сдвига исследуемой среды. Одно из тел на протяжении всего опыта остаётся неподвижным, другое, называемое ротором ротационного вискозиметра, совершает вращение с постоянной скоростью. Очевидно, что вращательное движение ротора визкозиметра передаётся к другой поверхности посредством движения вязкой среды. Отсюда следует вывод - момент вращения ротора ротационного вискозиметра является мерой вязкости.

Метод падающего шара основан на зависимости скорости свободного падения твёрдого шарика в вязкой жидкости и значением вязкости жидкости (например, вискозиметр Гепплера с падающим шариком).

Вязкость определяют также по затуханию периодических колебаний пластины, помещённой в исследуемую среду (ультразвуковой метод). Существуют автоматические системы измерения кинематической и динамической вязкости.

Растворение газов. Все жидкости в той или иной мере поглощают и растворяют газы. Относительное количество газа, которое может раствориться в жидкости до её насыщения, прямо пропорционально давлению на поверхности раздела. Объём газа W_г, растворённого в капельной жидкости до её полного насыщения, вычисляют по формуле:

W_г = k_гW_ж 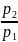, (1.15)

где W_ж – объём жидкости;

p₁ и p₂ – соответственно начальное и конечное давление на поверхности раздела жидкости и газа;

k_г – коэффициент растворимости газа в жидкости (объём газа, растворяющегося при атмосферном давлении и при t = 0 ºС в единице объёма жидкости).

Растворимость воздуха в реальной жидкости до её насыщения зависит от её вида и плотности. Предельные значения коэффициента растворимости k_г могут достигать 0,12…0,2. При температуре 20 ºС и атмосферном давлении в воде содержится 1,6% растворённого воздуха по объёму. При повышении температуры коэффициент растворимости уменьшается. При уменьшении давления из жидкости выделяется объём газа в соответствии с формулой (1.15). Процесс выделения газа протекает интенсивнее, чем растворение.

Испарение. Это свойство капельной жидкости изменять свое агрегатное состояние, в частности превращаться в пар. Интенсивность испарения (парообразования), происходящего на свободной поверхности жидкости, зависит от рода самой жидкости и условий, в которых она находится. Одним из показателей, характеризующих испаряемость жидкости, является температура её кипения при нормальном атмосферном давлении – чем выше температура кипения, тем меньше испаряемость. Кипение – это процесс перехода жидкости в газообразное состояние, происходящий внутри жидкости. Температура кипения с повышением давления на её поверхности увеличивается.

Если испарение происходит в свободном пространстве, то почти все молекулы, перешедшие при испарении в паровую фазу, удаляются с поверхности жидкости и обратно не возвращаются. Если жидкость находится в замкнутом пространстве, то после достижения в нём определенной концентрации паров устанавливается равновесие между процессами испарения и конденсации, и давление пара становится постоянным. Такой пар, находящийся в замкнутом пространстве в термодинамическом равновесии с жидкостью (число молекул, вырывающихся в единицу времени из жидкости и переходящих в паровую фазу, равно числу молекул, возвращающихся в жидкость за то же время), называют насыщенным. А его давление - давлением насыщенного пара при данной температуре. При этом давление пара и жидкости будет одинаковым.

В гидравлике наибольшее значение имеет условие, при котором начинается интенсивное парообразование по всему объёму жидкости. Обычно при понижении давления жидкости до давления насыщенных паров р_нп (при данной температуре) в жидкости образуются пузырьки газа, т.е. происходит так называемое «холодное кипение».

Зависимость р_нп воды от температуры приведена в таб. 2.

Таблица 2

Значения давления насыщенного пара для воды

в зависимости от температуры

t, ºС	рнп , МПа	t, ºС	рнп , МПа
0	0,0006	60	0,0202
10	0,0012	70	0,0317
20	0,0024	80	0,0482
30	0,0043	90	0,0714
40	0,0075	100	0,1033
50	0,0126	150	0,4850

Из данных, приведенных в таблице видно, что вода закипает при t = 100 ºС и атмосферном давлении (р_нп = р_ат). Однако, если давление на поверхности воды понизить до р = 12,6 кПа, а это значит, что давление внутри жидкости понизится до такого же значения (это давление будет меньше атмосферного в 8 раз), то вода закипит при температуре t = 50 ºС.

Представим, что жидкость течёт по трубопроводу, и попадает в зону пониженного давления, причём это давление будет ниже давления насыщенных паров жидкости при данной температуре. При этом растворённый в жидкости газ будет выделяться, образуя газовые полости (то есть произойдет процесс «холодного кипения»). Это явление получило название кавитация (от лат. «кавитас» – полость, введённое в обращение В. Фрудом).

Кавитация - это нарушение сплошности движущейся жидкости вследствие местного понижения давления ниже давления насыщенного пара при данной температуре.

В трубопроводе пузырьки, перемещаясь с потоком жидкости, попадают в область с высоким давлением или низкой температурой и мгновенно смыкаются. В этот момент пар конденсируется и газы снова растворяются в жидкости. В образовавшиеся пустоты с большими скоростями устремляются частицы жидкости, что приводит к местным гидравлическим ударам (резкому и значительному повышению давления в этих местах) и звуковым импульсам. Кавитация в обычных случаях является нежелательным явлением и приводит к:

- увеличению сжимаемости жидкости;

- уменьшению плотности;

- уменьшению пропускной способности трубопровода;

- повышению температуры жидкости;

- кавитационной коррозии металла.

Впервые с явлением кавитации встретились в судостроении в 1893 году при испытании английского миноносца «Дэринг». На режимах полного хода гребной винт резко изменял свои характеристики, что приводило к падению скорости корабля. С подобной проблемой столкнулись несколькими годами позже при испытании первого турбинного корабля «Турбиния».

Давление насыщенных паров жидкости является важным параметром, который необходимо учитывать, например, при расчётах систем водоснабжения с лопастными насосами. Определяют это давление с помощью различных автоматических анализаторов, термостатов. Большинство подобных аппаратов работает по принципу Рейда. Жидкостную камеру аппарата наполняют охлаждённой пробой испытуемого продукта и подсоединяют к воздушной камере при температуре 37,8 ºС. Аппарат погружают в баню с температурой (37,8 ± 0,1 ºС) и периодически встряхивают до достижения постоянного давления, которое показывает манометр, соединенный с аппаратом. Показание манометра, скорректированного соответствующим образом, принимают за давление насыщенных паров по Рейду.