3.8. Примеры решения задач

В данном разделе представлены примеры решения простейших задач, связанных с определением параметров движущейся идеальной жидкости. Основными уравнениями, позволяющими определить скорость, расход и давление движущейся идеальной жидкости, являются:

- уравнение постоянства расхода (3.3) ;

- уравнение Бернулли для идеальной жидкости без учёта потерь напора h_пот и коэффициента Кориолиса α (3.8)

.

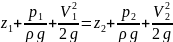Правила применения уравнения Бернулли рассмотрены в п. 3.5. Уравнение Бернулли рекомендуется вначале записать в общем виде, затем переписать его с учётом действующих в выбранных сечениях геометрического, гидростатического (или пъезометрического) и скоростного напора относительно плоскости сравнения. Члены уравнения, равные нулю, следует исключить. Также необходимо чётко представлять разницу между избыточным, вакуумметрическим и абсолютным давлением.

Рис. 3.20. Ртутный пъезометр

Если сечение выбирается в месте подключения ртутного пъезометра (рис. 3.20), то пъезометрическая высота будет равна:

,

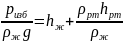где ρ_ж и ρ_рт – плотность жидкости в трубопроводе и ртути в пъезометре;

h_ж и h_рт – высота столба жидкости и ртути в пъезометре.

Задачи, связанные с течением жидкости в узких щелях, решают по формулам, представленным в п. 3.8.

Задача 3.9.1. Поршень диаметром d_п = 8 см перемещается со скоростью V_п под действием силы F = 0,4 кН. Жидкость плотностью ρ = 870 кг/м³ под действием поршня из правой части гидроцилиндра перемещается в бак, открытый в атмосферу. Определить скорость перемещения поршня V_п, если высота h = 9,4 м.

Рис. 3.21. Схема к задаче 3.9.1

Плоскость сравнения 0 – 0 выбираем по оси гидроцилиндра. Сечение 1 – 1 выбираем по живому сечению жидкости в гидроцилиндре, причём параметры уравнения, относящиеся к этому сечению, относятся к центру тяжести сечения. Сечение 2 – 2 выбираем по свободной поверхности жидкости, где давление – только атмосферное (избыточное р_изб = 0), скорость жидкости V₂ ≈ 0. Составим уравнение Бернулли, где давление будем учитывать в избыточной системе отсчёта.

Для сечения 1 – 1:

- геометрическая высота z₁ = 0, так как центр тяжести сечения совпадает с плоскостью сравнения;

- избыточное давление создаётся силой 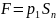, откуда

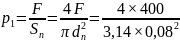= 80 кПа;

- жидкость в сечении движется с той же скоростью, что и поршень (V₁ = V_п), поэтому скоростной напор запишем как .

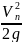Для сечения 2 – 2:

- геометрическая высота z₂ = h;

- избыточное давление р₂ = 0;

- скорость V₂ = 0.

Составим уравнение Бернулли:

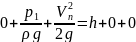, откуда

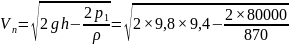= 0,576 м/с.

Задача 3.9.2. Определить вакуумметрическое давление в баке р_вак, при котором скорость течения потока жидкости в трубопроводе составит V_тр = 1,2 м/с. Высота h = 3,2 м, плотность жидкости ρ = 870 кг/м³. Высота уровня жидкости в пъезометре составляет h_п = 0,64 м.

Рис. 3.22. Схема к задаче 3.9.2

Плоскость сравнения 0 – 0 выберем по оси трубопровода в нижней его части. Сечение 1 – 1 выберем по установленному в нижней части трубы пъезометру, сечение 2 – 2 выберем по свободной поверхности жидкости в баке. Составим уравнение Бернулли, где давление будем учитывать в избыточной системе отсчёта.

Для сечения 1 – 1:

- геометрическая высота z₁ = 0, так как центр тяжести сечения совпадает с плоскостью сравнения;

- пъезометрическая высота в сечении ;

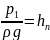- скорость течения жидкости в трубопроводе V₁ = V_тр.

Для сечения 2 – 2:

- геометрическая высота z₂ = h;

- вакуумметрическая высота ;

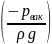- скорость V₂ = 0.

Составим уравнение Бернулли:

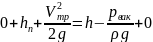, откуда

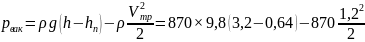= 21,2 кПа.

Задача 3.9.3. Определить утечки через радиальные зазоры в шестерённом насосе вследствие разности давлений в нагнетательной и всасывающей полости. Высота каждого зазора δ = 0,09 мм, длина зазора L = 2 мм, ширина В = 30 мм, перепад давлений ∆р = 1,32 МПа, наружный диаметр шестерни D = 62 мм, частота вращения n = 1450 об/мин, вязкость масла μ = 0,012 Па∙с.

Рис. 3.23. Схема к задаче 3.9.3

Считаем, что число зубьев, образующих радиальные зазоры слева и справа, одинаковы, и равны N = 7 с каждой стороны, размеры зазоров также одинаковы. Поэтому величина утечек слева и справа одинакова. Перепад давлений, приходящийся на один зазор, равен

.

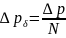Общий расход через зазоры равен сумме расходов слева и справа

.

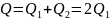Расход через зазоры слева или справа равен согласно (3.18)

.

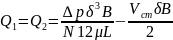Окружная скорость 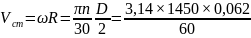= 4,7 м/с.

Тогда

=

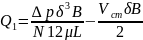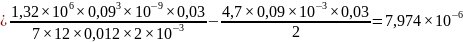м³/с.

Общий расход через зазоры вследствие утечек

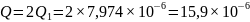м³/с ≈ 0,016 л/с.