2.2 «Обобщенные» критерии прочности
Более глубокое
обобщение теории прочности О. Мора
сделано М.М. Филоненко-Бородичем [8].
Сущность обобщения заключается в том,
чтобы искать функцию критерия предельного
состояния материала напряженного
состояния в окрестности с учетом
коэффициента Лодэ
напряженного состояния в окрестности
точки, т.е. перейти к учету влияния на
прочность промежуточного главного
напряжения:
где µ - коэффициент Лодэ, учитывающий вид напряженного состояния
в окрестности точки, - 1<µ<1.
Особое место
занимает критерий прочности
Давиденкова-Фридмана [3] , в котором четко
различаются два типа разрушения –
отрывом или сдвигом, причем утверждается,
что, в зависимости от условий проведения
опыта металл может разрушаться по одному
из этих механизмов. На этом основании
сделано предположение, что у металла
должно быть два параметра предельной
прочности – сопротивление отрыву и
сопротивление сдвигу, а самый простой
способ учета двойственного характера
разрушения металла – это рассматривать
одновременно действие касательных и
нормальных напряжений. В критерии
Давиденкова-Фридмана вводится предел
прочности по максимальному касательному
напряжению
(что допустимо только для пластических
материалов, например, металлов) и
предельное значение приведенных
растягивающих напряжений
.
На основании этого вводится новый
коэффициент
– коэффициент жесткости нагружения,
который равен отношению:
Приведенное растягивающее напряжение вычисляют по формуле Гука для наибольшего положительного удлинения, в котором оказался материал.
Если >1, - что означает превалирование касательных напряжений над приведенными растягивающими, - то нагружение считается мягким и разрушение материала будет вязким, т.е. от сдвига при малых удлинениях. Если <1, то нагружение считается жестким и происходит по механизму отрыва.
В качестве недостатков данного критерия разрушения в первую очередь укажем на невозможность его применения для материалов, которые не являются пластичными. Как известно, у этих материалов разрушение хрупкого типа происходит даже при отсутствии растягивающих напряжений в виде комбинации сдвигов и отрывов, что не вкладывается в схему Давиденкова-Фридмана.
В качестве одного из многочисленных критериев прочности, предложенных в виде комбинаций первого и второго инвариантов тензора напряжений, действующих в окрестности рассматриваемой точки, можно привести критерий Писаренко-Лебедева [13].
Здесь прослеживается близкая идейная аналогия с критерием Давиденкова-Фридмана, когда авторами введен дополнительный параметр 0<q<1 , с помощью которого можно описать условие прочности для пластического материала при разрушении от сдвига q=1 или для предела прочности от разрыва q=0.
2.3 .В. Новожилов установил в 1952 г., что эквивалентное напряжение по критерию пластичности потенциальной энергии изменения формы пропорционально квадратному корню из среднего значения квадратов касательных напряжений в точке, которое равно
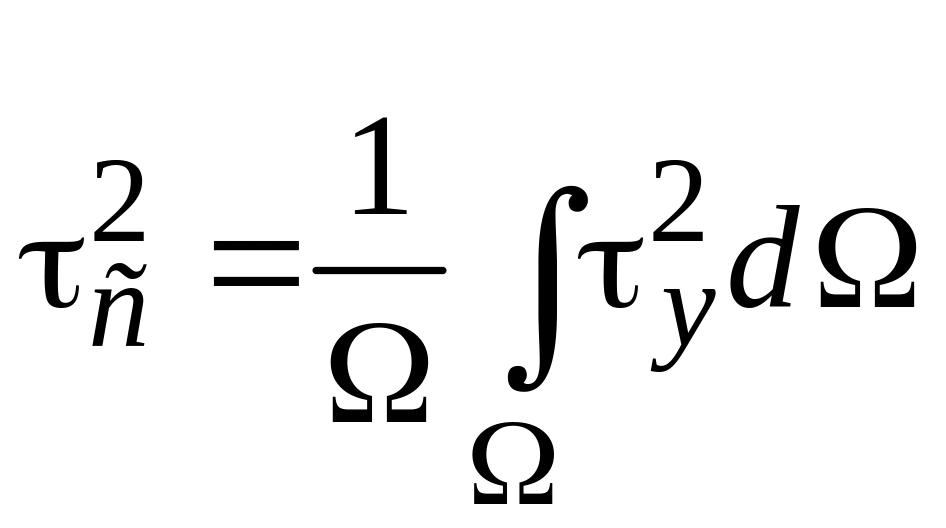
где dΩ — элементарная площадка сферы, Ω — площадь поверхности сферы, τy — касательное напряжение в площадке сферы с нормалью y.
Выбор сферы в качестве замкнутой поверхности, окружающей рассматриваемую точку тела, объясняется тем, что только на сфере (ввиду ее полной симметрии) будет в равной мере представлено все множество площадок, проходящих через точку.
2.4 Пономарев показал в 1955 г., что оно (эквивалентное напряжение) пропорционально квадратному корню из минимального среднеквадратичного уклонения главных напряжений заданного напряженного состояния от некоторого равноосного напряженного состояния
Исследование этой величины на экстремум приводит к заключению, что минимум ее имеет место при
и равен
Рассмотренные выше два критерия пластичности наибольших касательных напряжений и потенциальной энергии изменения формы справедливы для изотропного материала, у которого пределы текучести при растяжении и сжатии одинаковы.
2.5 Математик и механик Р.Хилл в 1950г. нашел, что если принять материал изотропным и имеющим одинаковые пределы текучести при растяжении и сжатии, то тогда геометрическим образом условия текучести является поверхность цилиндра, который в пересечении с девиаторной плоскостью дает 12одинаковых выпуклых дуг. Очевидно, что окружность Максвелла — Хубера является хорошей аппроксимацией этих дуг. Таким образом, условие потенциальной энергии изменения формы не является гипотезой, как это часто излагается в курсах сопротивления материалов, а может быть доказано с точностью до аппроксимации.
Если вокруг окружности Максвелла — Хубера описать правильный шестиугольник, то соответствующая призма в пространстве главных напряжений является геометрическим образом критерия пластичности наибольшего приведенного напряжения [210]. Этот критерий был впервые предложен в 1940 г. механиком Александром Юльевичем Ишлинским (06.08.1913) [178], а затем, в 1951г., — Р. Хиллом и Г. Уиллсом [380]. В курсах сопротивления материалов обычно этот критерий не приводится, поскольку экспериментальные точки, как правило, располагаются между шестиугольником Треска — Сен-Венана и окружностью Максвелла — Хубера. Однако решение упруго пластических задач на основе критериев Треска — Сен-Венана и Ишлинского — Хилла позволяет дать нижнюю и верхнюю оценки решения задачи, основанного на условии пластичности Максвелла — Хубера. Следует отметить, что решение по первым двум условиям принципиально проще, чем решения по условию Максвелла — Хубера, так как эквивалентные напряжения в них линейно зависят от главных напряжений в отличие от условия Максвелла — Хубера.
Девиаторная плоскость по Р. Хиллу
Дополнение (описание критериев прочности из другого источника)