
- •Зайцев ю.В., Мирошниченко а.Ю., Холодный д.С. Материалы и элементы электронной техники (физика процессов, строение и электрические характеристики)
- •Введение
- •1. Структура и строение материалов
- •1.1. Основные кристаллические структуры
- •1.2. Структуры бинарных соединений типа ав
- •1.3. Эффективные радиусы ионов и атомов
- •1.4. Геометрические пределы устойчивости структур с различными координационными числами
- •2. Процессы поляризации, диэлектрические потери
- •2.1. Комплексная диэлектрическая проницаемость
- •2.2. Уравнение электрического поля для изотропной среды
- •2.3. Электронная поляризация
- •2.4. Атомная и ионная поляризация
- •2.5. Ориентационная поляризация
- •2.6. Комплексная диэлектрическая проницаемость и уравнения Максвелла
- •2.7. Релаксационные потери
- •2.8. Физическая сущность диэлектрических потерь
- •3. Виды поляризация диэлектриков и диэлектрические потери
- •3.1. Виды поляризации
- •3.2. Простейшие схемы замещения диэлектриков с потерями
- •3.4. Тепловые виды поляризации
- •Зависимость от температуры параметров, описывающих тепловую поляризацию
- •Диаграмма коул-коула
- •3.4. Механизмы упругой поляризации.
- •3.5. Решеточное поглощение и отражение
- •4. Представление диэлектриков с помощью эквивалентных схем
- •4.1. Двух- и трех- элементные эквивалентные схемы
- •Входные характеристики
- •4.3. Схемы замещения реальных элементов электрических цепей
- •4.4. Поверхностная и объёмная поляризация
- •4.4. Измерение ε и tgδ
- •5. Классическая теория проводимости металлов
- •5.1. Основные предположения проводимости по теории Друде
- •5.2. Статическая электропроводность металла
- •6. Теория электропроводности Зоммерфельда
- •6.1. Распределения Максвелла − Больцмана и Ферми − Дирака
- •6.2. Свойства электронного газа в основном состоянии
- •6.2.1. Электрон как волна
- •6.2.2. Математическое описание волн
- •6.2.3. Уравнение Шредингера и волновая функция
- •7. Электропроводность диэлектриков и полупроводников
- •7.1. Электропроводность диэлектрических и полупроводниковых материалов
- •7.2. Диэлектрические керамические материалы
- •7.2.1. Алюминия оксид
- •7.2.2. Нанокристаллические материалы
- •7.2.3. Применение наноразмерных сегнетоэлектрических материалов
- •7.2.4. Пористая пьезокерамика
- •7.3. Полупроводниковые материалы
- •7.3.1. Типы полупроводников
- •7.4.2. Методы роста
- •7.5. Ионная проводимость
- •7.5.1. Диффузия ионов в электрическом поле
- •7.6. Зонная теория твердого тела
- •7.6.1. Стационарное уравнение Шредингера
- •7.6.2. Электрон в бесконечно глубокой потенциальной яме
- •7.6.3. Структула энергетических зон
- •7.6.4. Адиабатическое приближение и валентная аппроксимация
- •7.6.5. Одноэлектронное приближение
- •7.6.6. Трансляционная симметрия зон Бриллюэна
- •7.7. Колебания кристаллической решетки. Фононы
- •7.8. Теплоемкость твердых тел
- •8. Плёночные резисторы и конденсаторы
- •8.1.Конструкции и основные характеристики резисторов
- •8.2.Основные характеристики резисторов
- •8.3. Обозначения и маркировка резисторов
- •8.4. Специальные виды резисторов.
- •8.5. Конденсаторы
- •8.5.1. Конденсаторы с оксидным диэлектриком
- •8.5.2. Конденсаторы с органическим диэлектриком
- •8.6. Области использования конденсаторов
- •9. Коррозионная стойкость металлов
- •9.1. Виды коррозионных процессов
- •9.2. Физика процессов коррозии металлов
- •9.3. Образование продуктов окисления на поверхности металла
- •9.4. Основные стадии коррозии металлов
- •9.5. Адсорбция газов на поверхности металлов
- •9.6. Адсорбция кислорода на поверхности металла и образование оксида
- •9.7. Плёнки на поверхности металлов
- •9.8. Кинетика газовой коррозии металлов
- •9.9. Линейный закон роста плёнок
- •9.10. Параболический закон роста пленок
- •9.11. Сложные законы роста пленок
- •9.12. Оксидные пленки на поверхности металла
- •9.13. Механизм химической коррозии
- •9.14. Влияние внутренних и внешних факторов на скорость газовой коррозии
- •9.14.1. Влияние состава плёнки
- •9.14.2. Влияние температуры
- •9.14.3. Влияние давления и состава газа
- •9.15. Теории жаростойкого легирования
- •10. Металлические сплавы
- •10.1. Образование сплавов
- •10.2. Строение сплавов
- •10.3. Твердые растворы
- •10.4. Строение и свойства железоуглеродистых сплавов
- •10.5. Строение и свойства железа
- •10.6. Компоненты и фазы в сплавах системы (железо−углерод)
- •11. Магнитные материалы
- •11.1. Магнитные свойства твердых тел
- •11.1.1. Диамагнетики
- •11.1.2. Парамагнетизм
- •11.1.3. Ферромагнетики. Антиферромагнетики
- •1 ‒ Распределение в изолированных атомах; 2 ‒ распределение при обобществлении электронов.
- •11.2. Доменная структура
- •11.3. Намагничивание
- •11.4. Магнитострикция и термострикция
- •11.5. Ферримагнетизм. Ферриты
- •11.6. Процесс намагничивания.
- •11.6.1 Движение доменной стенки
- •11.6.2. Взаимодействие намагниченности с магнитным полем
- •11.6.3. Динамические эффекты процесса намагничивания
- •11.6.4. Перминвар - эффект
- •11.6.5. Магнитное последействие
- •11.7. Частотная зависимость магнитной проницаемости
- •Литература
2. Процессы поляризации, диэлектрические потери
2.1. Комплексная диэлектрическая проницаемость
Для конденсатора в вакууме (вакуумный конденсатор), подключенного к источнику синусоидального напряжения
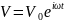 (2.1)
(2.1)
с угловой частотой
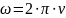 (2.2)
(2.2)
заряд конденсатора будет равен
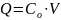 (2.3)
(2.3)
Зарядный ток можно записать в виде
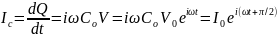 (2.4)
(2.4)
причем ток (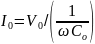 )опережает
напряжение по фазе на 90° (рис. 2.1). Емкость
вакуумного конденсатора (или геометрическую
емкость) обозначим через
)опережает
напряжение по фазе на 90° (рис. 2.1). Емкость
вакуумного конденсатора (или геометрическую
емкость) обозначим через
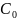 .
.
При замене вакуума каким−либо веществом
ёмкость конденсатора возрастает до
величины
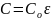 .
.

Рис. 2.1 Соотношение между током и напряжением в идеальном конденсаторе |
|
Рис. 2.2 Конденсатор, содержащий диэлектрик с потерями |
где
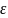 – действительная диэлектрическая
проницаемость или диэлектрическая
постоянная диэлектрика.
– действительная диэлектрическая
проницаемость или диэлектрическая
постоянная диэлектрика.
Одновременно, кроме компоненты зарядного
тока
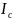 ,
может появиться компонента тока потерь
,
может появиться компонента тока потерь
 ,
рис. 2.3.
,
рис. 2.3.
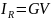 ,
(2.5)
,
(2.5)
которая находится в фазе с напряжением U. Величина G характеризует проводимость диэлектрика. Полный ток, проходящий через конденсатор, равен
 (2.6)
(2.6)
и составляет с напряжением U
угол
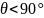 ,
определяемый коэффициентом мощности.
Угол δ (угол потерь) является дополнительным
до
,
определяемый коэффициентом мощности.
Угол δ (угол потерь) является дополнительным
до
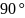 к оси
к оси
 (рис. 2.2).
(рис. 2.2).
Заключение, что диэлектрик по своим
электрическим свойствам соответствует
конденсатору с параллельно присоединенным
к нему сопротивлением (цепь
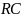 )
(рис. 2.3), является преждевременным.
Частотная характеристика этой цепи,
которая может быть выражена отношением
тока потерь
к зарядному току
)
(рис. 2.3), является преждевременным.
Частотная характеристика этой цепи,
которая может быть выражена отношением
тока потерь
к зарядному току
 ,
т.е. коэффициентом рассеяния или тангенсом
угла диэлектрических потерь
,
т.е. коэффициентом рассеяния или тангенсом
угла диэлектрических потерь
 ,
в виде
,
в виде
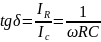 (2.7)
(2.7)

Рис.2.3. Цепь RC и её частотная характеристика
Расчетная частотная характеристика цепи вообще может и не совпадать с действительно наблюдаемой частотной характеристикой, потому что проводимость не всегда обуславливается движением носителей заряда, а может представлять любой другой процесс потребления энергии, например колебание дипольных молекул. Поэтому обычно, помимо зарядного тока, принято учитывать еще ток потерь путем введения комплексной диэлектрической проницаемости [9,10].
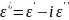 . (2.8)
. (2.8)
Тогда полный ток
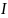 из уравнения (2.6) можно переписать в виде
из уравнения (2.6) можно переписать в виде
 ,
(2.9)
,
(2.9)
Тангенс угла потерь становится равным
 . (2.10)
. (2.10)
Поскольку плоскопараллельный вакуумный конденсатор с площадью пластин S и расстоянием между ними d без учета краевых эффектов имеет ёмкость
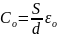 , (2.11)
, (2.11)
где
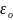 − относительная диэлектрическая
проницаемость, то плотность тока
− относительная диэлектрическая
проницаемость, то плотность тока
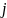 ,
проходящего через конденсатор при
напряженности поля
,
проходящего через конденсатор при
напряженности поля
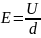 . (2.12)
. (2.12)
Согласно уравнению (2.8) с учетом: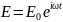 ,
,
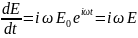 ,
,
плотность тока становится равной
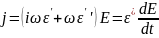 (2.13)
(2.13)
Произведение угловой частоты и коэффициента потерь определяет проводимость диэлектрика
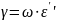 (2.14)
(2.14)
Проводимость диэлектрика складывается
из всех эффектов, связанных с диссипацией
энергии. Сюда относятся как истинно
омическая проводимость, вызванная
перемещением носителей заряда, так и
потери энергии, проявляющиеся в той
части зависимости
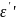 от частоты, которая учитывает трение,
возникающее при переориентации диполей.
от частоты, которая учитывает трение,
возникающее при переориентации диполей.
Итак, согласно такому рассмотрению схемы с сосредоточенными параметрами макроскопические электрические свойства диэлектриков описываются в синусоидальных полях с помощью комплексного параметра ε∗.
Действительная и мнимая части этой
комплексной переменной (соответственно
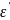 и
и
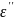 )
представляют собой соответственно
четные и нечетные функции переменной
ω, т.е. сопряженные функции, и поэтому
не являются совершенно независимыми
друг от друга. С точки зрения физики
механизмы накопления и рассеивания
энергии представляют две стороны одного
и того же явления; следовательно, если
один из них задается полным частотным
спектром, то этим определяется и другой.
В математике подсчет мнимой части
(сопряженной функции) по заданной
действительной части (произвольной
функции
)
представляют собой соответственно
четные и нечетные функции переменной
ω, т.е. сопряженные функции, и поэтому
не являются совершенно независимыми
друг от друга. С точки зрения физики
механизмы накопления и рассеивания
энергии представляют две стороны одного
и того же явления; следовательно, если
один из них задается полным частотным
спектром, то этим определяется и другой.
В математике подсчет мнимой части
(сопряженной функции) по заданной
действительной части (произвольной
функции
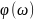 )
и наоборот описывается преобразованиями
Гильберта, известными физикам как
теорема Крамера. Это соотношение между
зависящими от частоты характеристиками
поляризации и потерь может иногда
оказаться полезным для проверки
правильности измерений, однако в общем
случае различные явления поляризации
и проводимости накладываются друг на
друга и доступный частотный диапазон
не достаточен для однозначного применения
данной теоремы [9].
)
и наоборот описывается преобразованиями
Гильберта, известными физикам как
теорема Крамера. Это соотношение между
зависящими от частоты характеристиками
поляризации и потерь может иногда
оказаться полезным для проверки
правильности измерений, однако в общем
случае различные явления поляризации
и проводимости накладываются друг на
друга и доступный частотный диапазон
не достаточен для однозначного применения
данной теоремы [9].
