1.Частные производные первого порядка

Z=f(x,y) ϵ D

Дадим переменным х,у прирощ. Δx, Δy

ΔxZ=f(x+Δx,y)-f(x,y)- приращ функции по переменной х

ΔyZ=f(x,y+Δy)-f(x,y) – приращ функции по переменной у

Δz=f(x+Δx,y+Δy)-f(x,y)- полное приращение функции)

Опр если существует 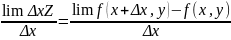, то его называют частн производной функции z=f(x,y) по переменной х

Обозн Zʼx=fʼx(x,y) =

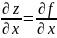
Частные производные Zʼx в точке M0 (x0,y0)

Обозн Zʼx (x0,y0) или fʼx (x,y)

Аналогично: Zʼу =

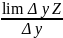
Из определения следует при нахождении Zʼx( Zʼу) переменная у(х) фиксируется

2.Частные производные высших порядков

2.Частные производные 2-го порядка называются Zʼʼxx=(Zʼx)ʼx, другие обозначения : fʼʼxx=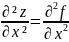 ,где

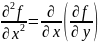
Zʼʼyy=(Zʼy)ʼy Zʼʼxy(Zʼx)ʼy Zʼʼyx=(Zʼy)ʼx

Частные производные по разн пременным называются смешанными

Теорема: Частные производные одного порядка равны т.е. не зависят от порядка диф. Для непрерывной функции

3.Опредление экстремума функции 2-х переменных. Необходимые и достаточные условия экстремума.

 

4. Дифференциальным Уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производные.

Решением ДУ называется функция, которая при подстановке в уравнение обращает его в тождество

Порядком ДУ называется наивысший порядок производной, входящий в ДУ

Если неизвестная функция зависит от одной переменной, то ее называют обыкновенной, в противном случае ДУ называют ДУ в частных производных.

ДУ n-го порядка имеет вид:

F(x, y, y’,y”,…, y^(n))

Если уравнение разрешимо относительно:

y^(n), то y^(n)=f(x, y ,y’, … , y^(n-1)) (2)

 

 

5. ДУ с разделяющимися переменныминазываются уравнения вида:

М1(х) N1(y)dx + M2(x)N2(x)dy=0 (1)

Умножим (1) на 1/N2(y)M2(x) =>

M1(x)dx/M2(x)+N2(y)dy/N1(y)=0 (6)

Уравнение (6)- ДУ с разделяющимися переменными

Интегрируя (6), получим ДУ

 

6.Функция f(x,y) называется однороднойфункцией к-го порядка, если для любого á € R

Выполняется f(Àx, Áy)=À^k(x,y)

В частности, если f(Àx,Ày)=f(x,y), то f(x,y)- однородная функция 0-го порядка

ДУ y’=f(x,y) называется однородной ДУ, f(x,y)- однородная функция 0-го порядка

ДУ P(x,y)dx+Q(x,y)dy=0 называется однородным ДУ, если 2 функции P(x,y) и Q(x,y) однородные функции одного порядка 

À-лямбда

 

7) Линейные дифференциальные уравнения первого порядка.

Определение: Линейным дифференциальным уравнением первого порядка называется уравнение вида:

Где P(x) и Q(x) – заданные функции.

Линейное дифференциальное уравнение решается методом Бернулли.

Полагаем , где u = u(x), v = v(x) – неизвестные функции и одна из этих функций выбирается производной ( т.к. , )

подставим в уравнение:

Полагаем:

Подставим в :

– общее решение.

8) Уравнение Бернулли.

Определение: уравнением Бернулли называется уравнение вида:

, где P(x), Q(x) – заданные функции, .

Уравнение Бернулли решается методом Бернулли т.е , где u = u(x), v = v(x) – неизвестные функции.

. Подставим в уравнение:

Полагаем:

Подставим в :

– общее решение.