3. Теорема куна-таккера

1. Предыстория: линейное программирование и принцип и метод Лагранжа

Рассмотрим неформально общую задачу оптимизации функций от n переменных 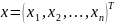: нахождение экстремума произвольной векторной функции при ограничениях, которые также задаются функциями. Далее оптимизируемые функции будем называть функциями ценности.

Как функции ценности, так и ограничения в первоначальной практической постановке могут не иметь формального аналитического вида. В этом случаем, произведём необходимое приведение с помощью интерполяции или других методов приближения. Заметим также, что имеет смысл выделять специальные представления, когда функции стоимости и ограничений имеют специальный вид, например: линейные, квадратичные, выпуклые.

Имеется два основных типа ограничений: равенства и неравенства, которые могут быть строгими и нестрогими. Особый тип представляют неравенства типа

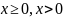. (3.1.1)

Для содержательного исследования этой задачи сделаем некоторые естественные упрощения:

• будем рассматривать оптимизацию только скалярных функций стоимости, т.е. исключим многокритериальные задачи, для которых пока не построена содержательная теория;

• будем рассматривать достаточно гладкие функции, а именно дважды непрерывно дифференцируемые 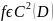для некоторого множества 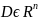, для которых ещё в XVIII веке Лагранж построил содержательную теорию на основе «множителей Лагранжа».

Теперь при этих условиях сделаем ещё модельные упрощения, чтобы лучше «прочувствовать» задачу.

Сначала рассмотрим тривиальный случай только линейных функций ценности и ограничений, и ограничения равенства. Тогда ограничения представляют собой систему линейных уравнений, теория которых хорошо известна. Чтобы эта система имела решения необходимо, чтобы число независимых ограничений m не превышало числа переменных n. Тогда её решения являются линейными функциями (формами) от максимального числа линейно независимых переменных, называемых базисом. Если эти выражения подставить в линейную функцию стоимости, то она станет зависимой только от этих m переменных, которая, очевидно, не ограничена как сверху, так и снизу. Либо в случае m=n будет стандартная система линейных уравнений с единственным решением или без решений в зависимости от значения определителя: неравного 0 или равного. Таким образом, в линейной задаче должны присутствовать ограничения неравенства.

Если рассматривать нелинейные функции, то ещё в XVIII веке Лагранж открыл и предложил принцип исследования задач с ограничениями равенствами, и соответствующий этому принципу метод решения. Расширение этого же метода до ограничений неравенств, произошло только в середине XX века и связано, прежде всего, с именами Куна и Таккера. Это расширения стало возможным только после постановки и решения задачи линейной оптимизации Канторовичем, и развитием этой теории в сторону теории игр Джоном фон Нейманом.

Далее рассматриваемая задача была обобщена на бесконечномерный случай для бесконечного числа переменных и соединилась с вариационным исчислением. В настоящее время теория в основном построена, но практически аналитические решения не существуют, так как задача сводится к решению систем нелинейных уравнений. Сложности возникают при численном решении практических линейных задач с большим и очень большим числом переменных или нелинейных функций с большой вариацией.

Начнём со всем известной классической теоремы Ферма о том, что в стационарных точках экстремума производная равняется 0, и этого достаточно в случае отсутствия ограничений. Когда появляются ограничения, то Лагранж предложил принцип виртуальных изменений для называемой функцией Лагранжа линейной комбинации функции стоимости и функций ограничений. Эти виртуальные изменения параметризуются, так называемыми, множителями Лагранжа 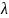, и экстремум задачи соответствует экстремуму функции Лагранжа и коллинеарности градиентов функции стоимости и линейной комбинации ограничений. При этом такое сведение к функции Лагранжа удаётся не всегда, и это называется нерегулярным случаем с нерегулярными точками, где это происходит.

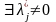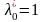Как мы уже видели выше, в случае множителя Лагранжа , соотношения принципа Лагранжа лишь говорят о некоторой вырожденности ограничений (т.е. о том, что часть ограничений можно исключить), и об отсутствии их связи с функцией стоимости. Таким образом, годятся только такие решения уравнений для стационарных точек, в которых . В случае для задачи на минимум можно положить , а в задаче на максимум .

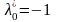Принцип Лагранжа может давать эффективные результаты даже для многих экстремальных задач, имеющих другую постановку, для которых он не является строго обоснованным. Т.е. имеет смысл применять принцип Лагранжа, связанный с проверкой стационарных точек функции Лагранжа.