3.9. Теорема Куна-Таккера

Формулы (3.8.2)-(3.8.7) составляют содержание теоремы Куна-Таккера, только в отличие от предыдущего параграфа, где функция была произвольной, в данном случае она является функцией Лагранжа для задачи максимизации нелинейного программирования, а (х_опт,λ_опт) - точка экстремума. Сама теорема может быть сформулирована следующим образом: соотношения (3.8.2)-(3.8.7) являются необходимыми и достаточными условиями, для того чтобы точка х_опт представляла собой решение задачи выпуклого нелинейного программирования:

max {F(x)|x_j≥0, j=1,...,n; φ_i(х)≤b_i, i = 1,...,m}. (3.8.29)

Сведем исходную задачу к классической постановке. Для этого прежде всего ограничения-неравенства φ_i(х)≥b_i сведем к равенствам, введя и переменных x_φi ≥0 (i = 1,2,..., u), соответствующим неравенствам. Остальные m – u ограничений считаются строгими равенствами. Тогда

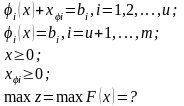(3.8.30)

Тем самым допускается, что часть из m неравенств имеет вид строгих равенств.

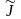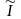Предположим, что для этой задачи х = х_опт. Обозначим через J множество индексов j (j = 1, ..., n) для которых x_jопт > 0, а через  – множество индексов j, для которых x_jопт = 0. Аналогично будем считать, что I - множество индексов i (i = 1, ..., u) для которых φ_i(х_oпт) = b_i,   – множество, состоящее из индексов i, для которых ограничения на φ_i(х_опт) выполняются со знаком строгого неравенства φ_i(x_опт)<b_i. Заметим, что речь идет только о точке оптимума х_опт и знак нестрогого неравенства "≥" теряет свой смысл и соотношение превращается или в строгое неравенство (типа 5>4) или в строгое равенство (типа 3=3). На основании результатов, полученных в § 17-3, можем написать, что

(3.8.31)

так как множество J соответствует внутренней области допустимых значений, и λ_iопт = 0 , 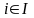, так как множество I соответствует ограничениям в виде строгих неравенств, которые можно не учитывать. Далее

(3.8.32)

так как множество J соответствует границе области допустимых значений.

Соотношения (3.8.31) и (3.8.32) обеспечивают выполнение условия (3.8.2)

(3.8.33)

Теперь нетрудно убедиться, что

(3.8.34)

Это соотношение обеспечивает выполнение формулы (3.8.3). Затем имеем:

(3.8.35)

так как множество I соответствует границе области. Эти разности неотрицательны, а остальные n - u равны нулю по условию. Формула (3.8.35) обеспечивает выполнение условия (17-23), которое по существу совпадает с ограничениями в исходной задаче нелинейного программирования. Наконец, условие (17-24) выполняется в силу доказанных ранее соотношений (17-17), согласно которым для ограничений в виде строгих неравенств

(3.8.36)

соответствующий множитель Лагранжа λ_i = 0 и λ_i ≠ 0 только при

(3.8.37)

Таким образом, доказано, что в точке оптимума задач нелинейного программирования выполняются необходимые и достаточные условия существования седловой точки (необходимость теоремы Куна - Таккера). Для доказательства достаточности этой теоремы необходимо дополнительно потребовать выпуклости (вогнутости) и использовать методы доказательства достаточности условий (3.8.2)-(3.8.7) для существования седловой точки. Тем самым доказана теорема Куна - Таккера для случая дифференцируемых функций.

В литературе имеются доказательства этой теоремы для не дифференцируемых функций F(х) и φ_i(х). В этом случае теорема формулируется следующим образом: вектор х_опт тогда и только тогда является решением задачи (3.8…..), когда существует вектор λ_опт, такой, что справедливы соотношения

x_опт≥0; λ_опт≥0; (17-40)

Φ (x_опт, λ) ≥ Φ (x_опт, λ_опт) ≥ Φ (х, λ_опт) (3.8.38)

для всех х≥0 и λ≥0, т. е. задача о максимизации f (х) соответствует задаче о седловой точке, иными словами, задаче о максимине для функции L(х, λ).