Лабораторные работы / лаба5чм

Московский Энергетический Институт (Технический Университет)

Дисциплина: Численные методы

Лабораторная работа №5

Тема: Решение систем нелинейных уравнений.

Вариант 10

(задачи 5.2,5.3)

Студент группы А-14-06

Лозинский Павел

Задача 5.2

Постановка задачи: Плоская однородная пластина имеет форму геометрической фигуры, образованной пересечением двух кривых второго порядка. Определить площадьфигуры.

Первая кривая – гипербола, её уравнение:

_{Вторая кривая – эллипс. Заданы координаты его фокусов и постоянная а:}

Основное решение: По определению, эллипс – геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная. Составим уравнение, используя формулу расстояния между двумя точками и исходные данные:

Чтобы построить график этой функции, разрешим это уравнение относительно переменной Х, с помощью пакета MATHCAD:

Теперь можно построить её график, а также график исходной кривой:

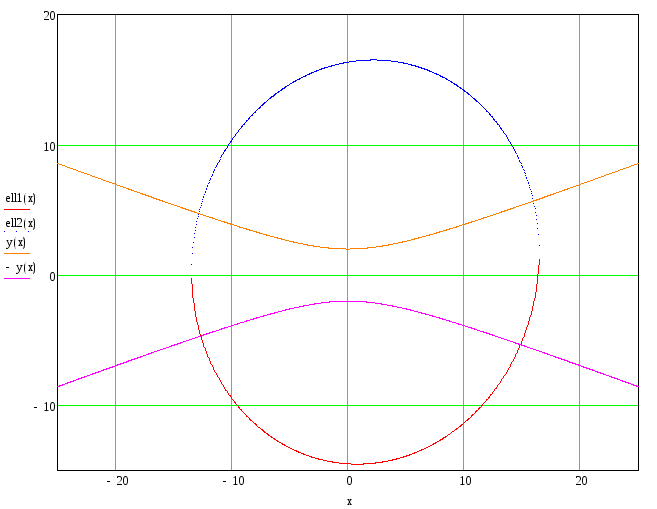
Из графика видно, что в качестве начального приближения можно взять точки с координатами

(-13,5), (-13,-5), (15,-5), (16,6)

Для поиска приближения будем использовать следующую функцию:

Здесь А – матрица из производных, имеющая следующий вид:

Таким образом, имеем границы интегрирования.

а1= -13.8821325935 b1=16.0687717793

а2= -13.3257237192 b2=14.0597302542

Найдем площади фрагментов:

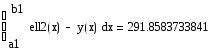
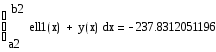
Взяв модуль второго интеграла (т.к. график интегрируемой функции расположен ниже оси абсцисс) и просуммировав их, получим требуемый результат.

Задача 5.3

Постановка задачи: Для системы уравнений из задачи 5.1 найти решение по методу простой итерации с той же точностью . Для этого составить программу вычисления решения с заданной точностью. В программе предусмотреть подсчет количества итераций, потребовавшихся для достижения заданной точности. Сравнить скорости сходимости методов. Достаточное условие сходимости метода проверить в норме .

Заданная система уравнений имеет следующий вид:

Основное решение: Разрешим оба уравнения относительно переменной х1:

и построим их графики с целью локализации корня:

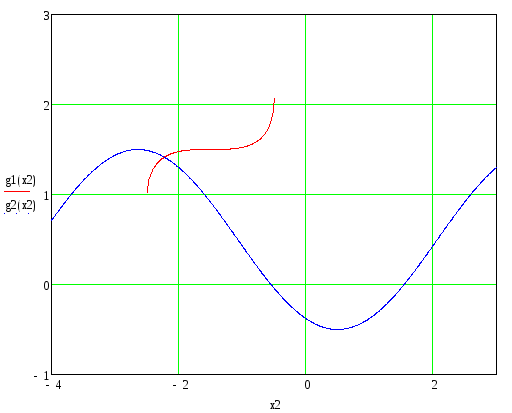
В качестве начального приближения, как видно из графика, можно взять точку с координатами

х1=1.4 и х2=-2.2.

В методе простой итерации исходная система:

F1(x1,x2…xn)=0

F2(x1,x2…xn)=0

………………...

Fn(x1,x2…xn)=0

Преобразуется к системе вида:

x1=φ1(x1,x2,…xn)

x2=φ2(x1,x2,…xn)

…………………

xn=φn(x1,x2,…xn)

И для метода простой итерации справедлива расчетная формула:

Х^(к+1)= φ(Х^(к)), где Х^(к) есть вектор к-го приближения, а φ – вектор-функция.

Преобразуем нашу исходную систему к виду, удобному для итерации:

Достаточным условием сходимости метода простой итерации является то, что норма матрицы Якоби в точке начального приближения будет меньше единицы. Матрица Якоби – матрица, состоящая из производных функций по всем аргументам.

Составим матрицу Якоби:

Посчитаем бесконечную норму этой матрицы, взятой в начальном приближении:

Достаточное условие сходимости не выполнено. Однако метод все равно сойдется.

Критерий окончания метода простой итерации:

Здесь q0 – норма матрицы Якоби, взятая в начальном приближении.

Рассчитаем требуемую точность и обозначим её за ε1:

Опишем функцию, для метода простой итерации:

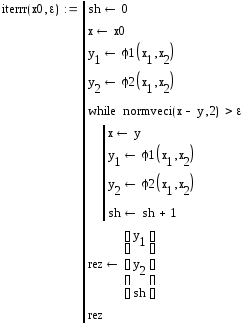
Возьмем в качестве х0 вектор (1.4, -2.2) и исполним функцию:

Таким образом, метод сошелся с необходимой точностью за 17 итераций.

10