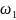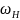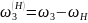- •Қазақстан республикасы білім және ғылым министрлігі қ.Жұбанов атындағы ақтөбе өңірлік мемлекеттік университеті
- •5B071300 «Көлік, көлік техникасы және технологиясы»
- •2Курс студенттеріне арналған
- •Әдістемелік нұсқаулық
- •Машинаның шағын анықтамасы.
- •1. Жазық механизмдер структурасы.
- •1.1 Жазық кинематикалық жұптың классификациясы. Байланыс шарттарының саны бойынша классификациясы.
- •Элементтердің жанасу сипатына қарай классификациясы.
- •1.2. Жазық механизмнің қозғалу мүмкіндігін есептеу.
- •1.3. Механизмнің структуралық классификациясы. Механизмнің структуралыққұрылымы үшін л.В. Ассур принципі.
- •Ассургруппасы және олардың классификациясы.
- •II класс III класс IV класс V класс
- •Механизмніңклассификациясы. Механизмнің құрылым формуласы.
- •1.4. Жазық механизмдегі жоғарғы жұпты алмастыру.
- •1.5. Артық (қайталанатын) байланыс және механизмдегі жергілікті қозғалыс.
- •2. Тісті механизмнің кинематикасы
- •2.1. Берiлiс қатынасы туралы ұғым
- •2.2. Жай тісті берілістің беріліс қатынасы.
- •2.3. Қозғалмайтын біліктітісті доңғалақты механизмнің кинематикасы.
- •Доңғалақтары қатарқосылысты механизм.
- •Доңғалақтары сатылы қосылысты механизм.
- •2.4. Планетарлы типтімеханизмнің кинематикасы.
- •Эпицикликалық механизмнің типтік схемасы.
- •Кинематиканың аналитикалық есебі.
- •Кинематиканың графикалық есебі.
- •3. Эвольвенталық тiстi iлiнiс
- •3.1. Ілiнiсудің негізгі заңы.
- •3.2. Шеңбердің эвольвентасы, оның қасиеті мен теңдеуі.
- •Эвольвентаның қасиеттері.
- •Эвольвента теңдеуі.
- •3.3. Тісті дөңгелектің элементтері.
- •3.4. Эвольвентті ілінісудің элементтері мен қасиеттері.
- •Ілінісу қасиеттері.
- •3.5. Эвольвентті ілінісудің сипаттамалары. Қосарлама коэффициентi.
- •Меншікті сырғанау.
- •Меншікті қысым коэффициенті.
- •3.9. Тісті доңғалақты жону үшін ығысу коэффициентін тағайындау.
- •3.6. Тісті доңғалақтың геометриялық өлшемдерін есептеу.
- •Ілінісу бұрышы.
- •Бастапқы шеңбер радиусы және осьаралық қашықтық.
- •Ойық шеңбердiң радиустары.
- •Тіс басы шеңберінiң радиустары.
- •Бөлгіш шеңбер бойынша тістің қалыңдығы.
- •Бақылау сұрақтары:
- •4. Төменгі кинематикалық жұпты механизмніңкинематикасы.
- •4.1. Зерттеудің мақсаты.
- •4.2.Аналитикалық әдіс.
- •4.3. Орналасу орнының, жылдамдықтың және үдеудің Метод планы әдісі.Орналасу орнының функциясын анықтау.
- •Жылдамдық пен үдеуді анықтау.
- •4 .4. Кинематикалық диаграмма әдісі (графикалық дифференциалдау әдісі).
- •5. Механизмнің кинетостатикасы.
- •5.1. Инерция күшін есептеу.
- •Звеноның ілгерлемелі қозғалысы.
- •Звеноның айналмалы қозғалысы.
- •Звеноныңжазық –параллельқозғалысы.
- •5.2. Күштiк есептің жалпы ережелері.Даламбер принципі.
- •Босату принципі.
- •Ассур группасыныңстатикалық анықталатындығы.
- •5.3. Кинематикалық жұптағы реакцияны анықтаудың күш жоспары әдісі.Ассургруппасының күштік есебі.
- •Кривошиптің күштік есебі.
- •5.4. Теңестіруші күшті н.Е. Жуковский әдісімен анықтау.
- •6. Машина динамикасы.
- •6.1. Машина динамикасының қосымша мақсаты. Машинаныңдинамикалық моделі.
- •Келтірілген инерция моменті.
- •Кедергі күшінің келтірілген моменті.
- •6.2. Машина қозғалысы режимдерінің сипаттамасы.
- •II. Қалыптасқан режим
- •6.3. Машина қозғалысының теңдеуі. Машина қозғалысының теңдеуініңинтеграл формасы.
- •Машина қозғалысының теңдеуініңдифференциал формасы.
- •6.4. Маховиктің инерция моментінің жуықтау есебі және оның мақсаты.
- •Әдебиеттер:
Доңғалақтары сатылы қосылысты механизм.
Бұл механизмде доңғалақ колеса параллель жазықтықта айналады және әр аралық доңғалақ тек бір көрші доңғалақпен ілініске түседі. Әр аралық білікте екі доңғалақ болады.

2.3-ші сурет
2.3-ші
суретте механизмнің схемасы көрсетілген,
онда аралық білікте 2 және 3, 4 және 5, 6
және 7 доңғалақтары айналады, жетекші
біліктетек 1-ші доңғалақ, ал жетектегі
білікте-8-ші доңғалақ.1-ші
доңғалақтан 8-ші
доңға-лаққа дейінгі беріліс қатынасын
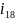 анықтаймыз. Ол үшін алдымен жазамыз:
анықтаймыз. Ол үшін алдымен жазамыз:
 .
.
,
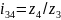 ,
,
 және
және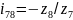 болғандықтан, бұл бөлшектерге беріліс
қатынасының көбейтіндісін қою арқылы
қортынды теңдеуді аламыз:
болғандықтан, бұл бөлшектерге беріліс
қатынасының көбейтіндісін қою арқылы
қортынды теңдеуді аламыз:
 .
.
2.4. Планетарлы типтімеханизмнің кинематикасы.
Қаралған механизмдер схемасынан бөлек механизмдер схемасы болады, олардың айырмашылығы кейбір доңғалақтың біліктері қозғалмалы.Бұндай механизмпланетарлы немесе эпицикликалық типті механизмге жатады. Бұл механизмдер беріліс қатынасы бойынша тиімді, себебі олар, доңғалақтың аз санының өзінде үлкен беріліс қатынасын қамтамасыз ете алады.
Эпицикликалық механизмнің типтік схемасы.
2.4-ші суретте типтік схеманың бірі көрсетілген. Онда сыртқы тістері бар центрлік доңғалақ 1, ішкі тісті күн доңғалағы деп аталатын центрлік доңғалақ 3 және сателлит деп аталатын доңғалақ 2. Сателлит деп аталу себебін,ол араласатын екі айналмалы қозғалыстан алып отыр: өз білігі бойымен айналу және механизмнің ортақ осі бойымен айналу. Бұндай мүмкіншілікті сүйрегіш деп аталатын стержень типті звено береді.

2.4-ші сурет
Егер
екі
центрлікдоңғалақайналатын
болса,
онда
механизмде жәнедифференциалдеп
аталады.
жәнедифференциалдеп
аталады.
Егер
центрлікдоңғалақтың
біріайналмайтын болса,
онда ,
және меха-низм
планетарлық
деп
аталады.
,
және меха-низм
планетарлық
деп
аталады.
Кинематиканың аналитикалық есебі.
Кинематиканың аналитикалық есебінде дифференциалды механизмдегі жетекші звеноның берілген бұрыштық жылдамдығы бойынша жетектегі звено-ның бұрыштық жылдамдығы анықталады, ал планетарлы механизмде, қозға-лысты өңдеу әдісі бойынша жетекші звено мен жетектегі звеноның беріліс қатынасы анықталады. Бұл әдіс бойынша, тірекпен бірге барлық механизмгесүйрегіштің бұрыштық жылдамдығына қарсы бағытталған бұрыштық жылдам-дықпен қозғалыс беріледі. Звенолардың салыстырмалы қозғалысының сипат-тамасы сақталған кезде, сүйрегіш тоқтайы, ал қалған звенолардың бұрыштық жылдамдықтары сүйрегіштің бұрыштық жылдамдығына азаяды. Бұл жағдай-да механизм, доңғалығының қозғалмайтын білігі бар шартты механизмге айналады. Онда жылдамдықтың келесі таблицасын құруға болады:
Звено № |
нақты механизмдегі звенолардың бұрыштық жылдамдығы |
доңғалығының қозғалмайтын білігі бар шартты механизмнің звеноларының бұрыштық жылдамдығы |
1 2 3
|
|
|
Сүйрегіш
қоғалмайды деген шартпен, бірінші
центрлік
доңғалақтан үшінші доңғалаққа қатысты
беріліс қатынасын
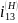 жазамыз.
2.4-ші суретте көрсе-тілген схема үшін:
жазамыз.
2.4-ші суретте көрсе-тілген схема үшін:
 ,немесе
таблицадан сәйкес айырмашылықты
қойғаннан кейін келесі теңдеуді аламыз:
,немесе
таблицадан сәйкес айырмашылықты
қойғаннан кейін келесі теңдеуді аламыз:
 .
(а)
.
(а)
Теңдеудің сол жағындағы үш шаманың екеуі белгілі болуы шарт, ал үшіншісі теңдеуді шешу арқылы анықталады.
Планетарлы
механизмде, жоғарыда көрсетілгендей,
центрлік доңғалақтың бірі қозғалмайды.
Егер ішкі тістері бар 3-ші доңғалақты
қозғалмайды деп есеп-тесек, яғни ,
онда (а) теңдекті келесі түрде жазуға
болады:
,
онда (а) теңдекті келесі түрде жазуға
болады:
 .
Теңдеудің алымы мен бөлімін мүшелерге
бөліп және бұрыштық жылдам-дық қатынасын
беріліс қатынасын алмастыру арқылы
қортынды теңдеуді ала-мыз:
.
Теңдеудің алымы мен бөлімін мүшелерге
бөліп және бұрыштық жылдам-дық қатынасын
беріліс қатынасын алмастыру арқылы
қортынды теңдеуді ала-мыз:
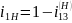 ,
(б)
,
(б)
Яғни, планетарлы механизмдегі кез келгенцентрлік доңғалақтан сүйре-гішке қатыстыберіліс қатынасы бірден осы центрлік доңғалақтан, меха-низмдегі шартты қозғалмайтын сүйрегіші бар бөтен центрлік доңғалаққа қатысты беріліс қатынасын алып тастағанға тең болады.