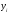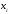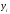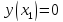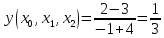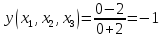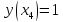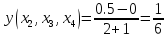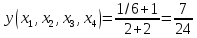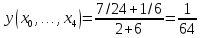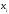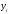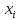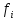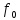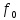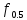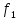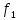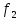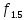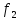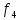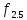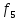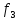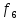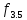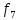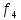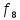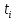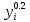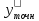Типовые расчёты
.docxЗахаров Антон, А-13-08
Типовой расчёт № 12
Вариант № 10
Функция
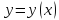задана таблицей своих значений. Применяя
метод наименьших квадратов приблизить
функцию многочленами 1-ой и 2-ой степеней.
Для каждого приближения определить
величину среднеквадратичного приближения.
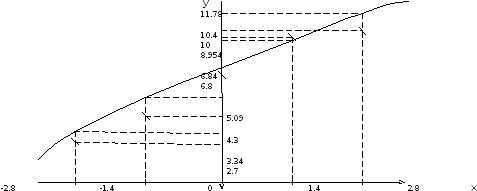
Построить точечный график функции и
графики многочленов.
|
|
-2.8 |
-1.4 |
0 |
1.4 |
2.8 |
|
|
2.7 |
4.3 |
6.8 |
10 |
10.4 |
Решение.
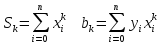
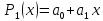
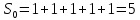
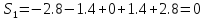
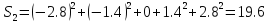
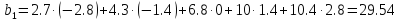
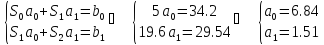
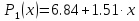
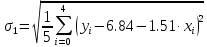
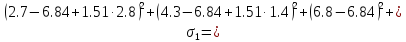
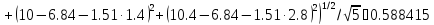
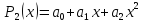
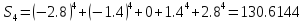
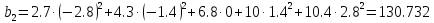
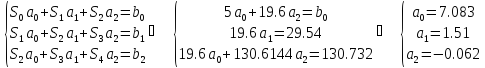
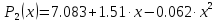
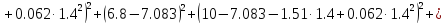
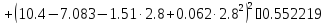
Захаров Антон, А-13-08
Типовой расчёт № 13
Вариант № 10
Вывести
нормальную систему уравнений для
определения коэффициентов
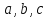функции
,
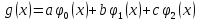осуществляющей среднеквадратичную
аппроксимацию таблично заданной функции
.
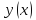Значения
функции
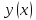в
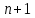точках
считать известными.
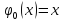
Решение.
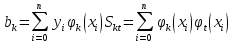
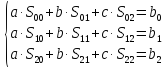
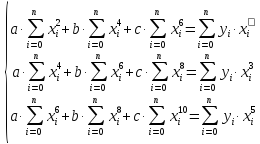
Захаров Антон, А-13-08
Типовой расчёт № 14
Вариант № 10
Для
функции
,
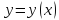заданной таблицей своих значений,
построить интерполяционные многочлены
в форме Лагранжа и Ньютона. Используя
их, вычислить приближенное значение
функции в точке
.
|
|
-3 |
-2 |
-1 |
|
|
0 |
2 |
2 |
Решение.
Многочлен Лагранжа:
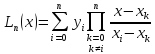
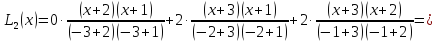
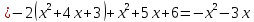
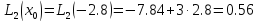
Многочлен Ньютона:
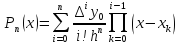
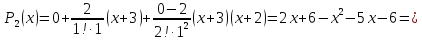
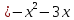
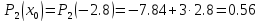
Захаров Антон, А-13-08
Типовой расчёт № 15
Вариант № 10
Для
функции
,
заданной таблицей своих значений
построить интерполяционный многочлен
Ньютона. С его помощью вычислить
приближенное значение функции в точке
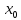и дать практическую оценку погрешности.
Записать результат с учётом погрешности.
|
|
-4 |
-2 |
-1 |
0 |
2 |
|
|
-6 |
0 |
2 |
2 |
1 |
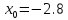
Решение.
Составим диагональную таблицу разделённых разностей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
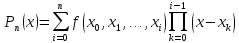
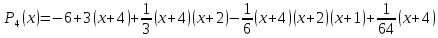
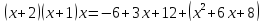
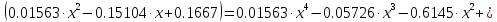
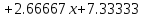
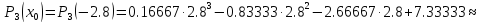
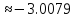
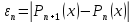
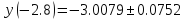
Захаров Антон, А-13-08
Типовой расчёт № 16
Вариант № 10
Функция
,
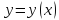задана таблицей своих значений:
|
|
0 |
1 |
2 |
3 |
|
|
-5 |
3 |
14 |
27 |
Построить
параболический сплайн дефекта 1 для
функции
,
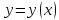если известно также дополнительное
условие
.
На
одном чертеже построить график сплайна
и указать исходные точки
.
Решение.
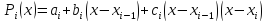
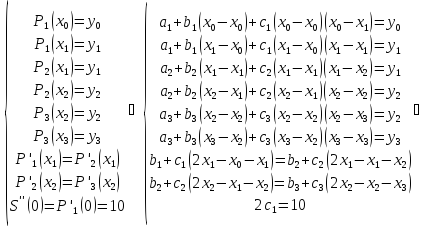
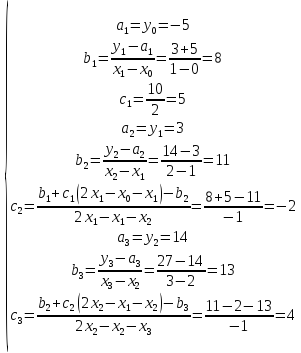
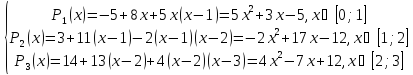
Захаров Антон, А-13-08
Типовой расчёт № 19
Вариант № 10
Вычислить
приближенное значение интеграла
,
используя квадратурные формулы:
-
центральных прямоугольников с шагом h = 0.4; дать априорную оценку погрешности;
-
трапеций с шагами h = 0.4 и h = 0.2; оценить погрешность последнего результата по формуле Рунге и уточнить последний результат по Рунге;
-
Симпсона с шагом h = 0.4.
Решение.
|
i |
|
|
|
|
|
0 |
0.9 |
0.837388 |
|
|
|
1 |
1.1 |
0.782110 |
|
|
|
2 |
1.3 |
0.750226 |
|
|
|
3 |
1.5 |
0.730284 |
|
|
|
4 |
1.7 |
0.716935 |
|
|
|
5 |
1.9 |
0.707633 |
|
|
|
6 |
2.1 |
0.700822 |
|
|
|
7 |
2.3 |
0.695762 |
|
|
|
8 |
2.5 |
0.691822 |
|
|
а)
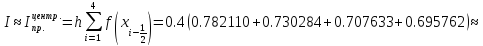
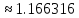
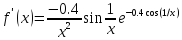
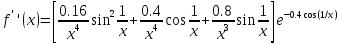
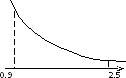
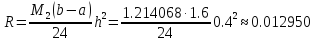
б)
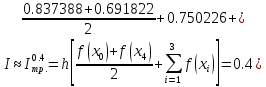
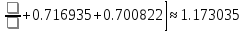
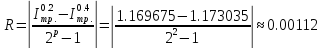
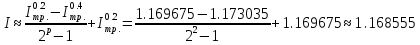
в)
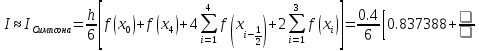
Захаров Антон, А-13-08
Типовой расчёт № 20
Вариант № 10
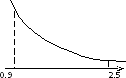
Определить
шаг, достаточный для вычисления интеграла
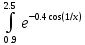с точностью
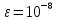по формуле трапеций.
Решение.
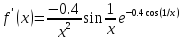
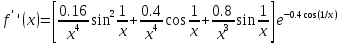
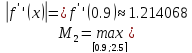
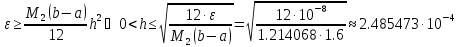
Захаров Антон, А-13-08
Типовой расчёт № 21
Вариант № 10
Построить квадратурную формулу вида
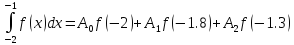
точную для многочленов степени 0, 1, 2 методом неопределённых коэффициентов.
Решение.
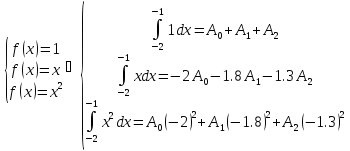
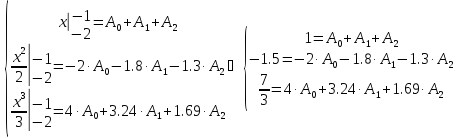
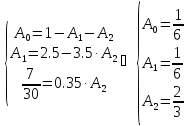
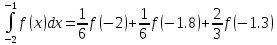
Захаров Антон, А-13-08
Типовой расчёт № 22
Вариант № 10
Вычислить
центральную и правую разностные
производные функции
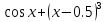с шагом
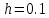в точке
.
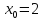Выполнить априорную оценку погрешности
для каждой формулы, сравнить с точным
значением производной.
Решение.
Центральная
разностная производная:
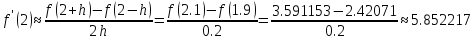
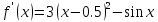
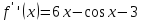
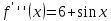
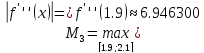
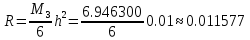
Правая разностная производная:
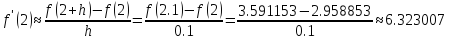
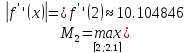
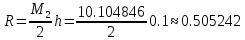
Точное значение производной:
Захаров Антон, А-13-08
Типовой расчёт № 23
Вариант № 10
Определить порядок аппроксимации формулы численного дифференцирования
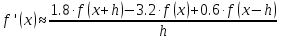
Решение.
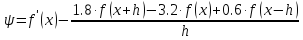
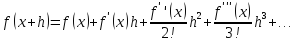
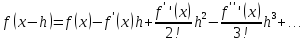
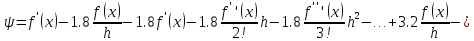
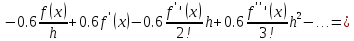
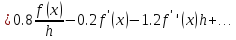
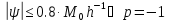
Захаров Антон, А-13-08
Типовой расчёт № 24
Вариант № 10
Численно решить задачу Коши для обыкновенного дифференциального уравнения I-ого порядка
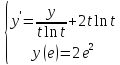
на
отрезке
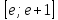с шагом
:
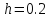а) методом Эйлера; б) методом Рунге-Кутты
2-ого порядка с оценкой погрешности по
правилу Рунге. Найти точное решение
задачи. Построить на одном чертеже
графики точного и приближенных решений.
Решение.
а) Метод Эйлера.
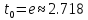
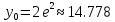
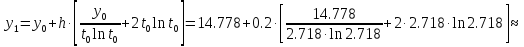
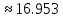
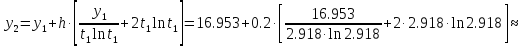
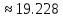
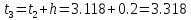
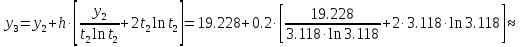
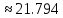
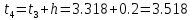
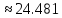
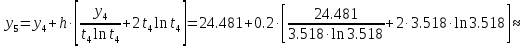
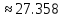
б) Метод Рунге-Кутты 2-ого порядка с оценкой погрешности по правилу Рунге.
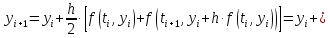
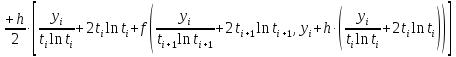
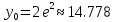
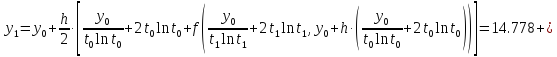
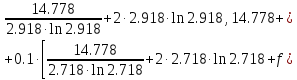
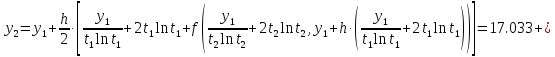
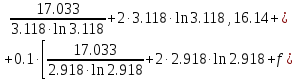
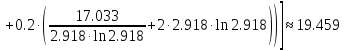
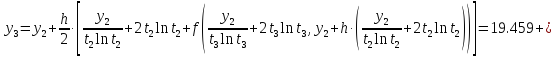
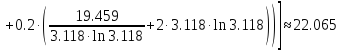
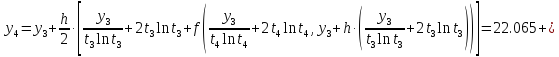
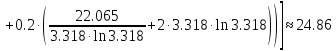
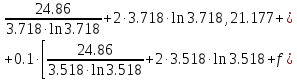
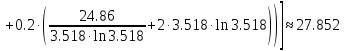
Аналогично посчитаем для шага h = 0.1.
|
|
2.718 |
2.918 |
3.118 |
3.318 |
3.518 |
3.718 |
|
|
14.778 |
17.033 |
19.459 |
22.065 |
24.86 |
27.852 |
|
|
14.778 |
17.034 |
19.461 |
22.068 |
24.865 |
27.858 |
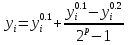
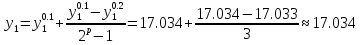
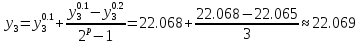
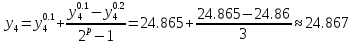
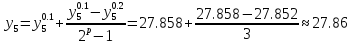
Точное решение.
|
|
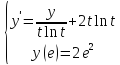
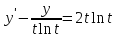
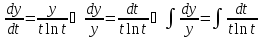
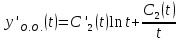
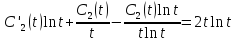
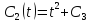
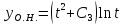
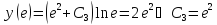
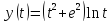
2.718 |
2.918 |
3.118 |
3.318 |
3.518 |
3.718 |
|
|
14.778 |
17.035 |
19.462 |
22.07 |
24.867 |
27.86 |
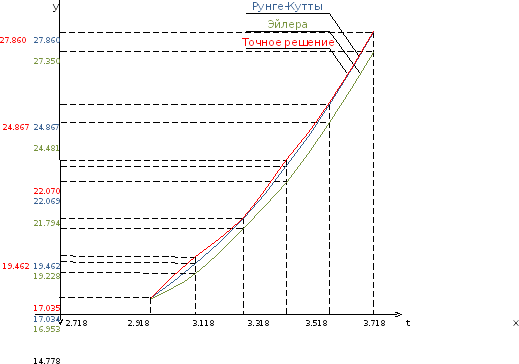
Захаров Антон, А-13-08
Типовой расчёт № 25
Вариант № 10
Исследовать 2-шаговый метод решения задачи Коши для ОДУ I-ого порядка
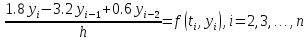
на нуль-устойчивость.
Решение.
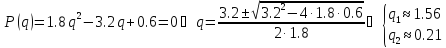
Метод не является нуль-устойчивым, так как не выполнено корневое условие (один из корней характеристического полинома метода лежит вне комплексной плоскости радиуса 1).
Захаров Антон, А-13-08
Типовой расчёт № 28