Замена переменных в тройном интеграл

Если в тройном интеграле , производится замена переменных по формулам x = x(u, v, w), y = y(u, v, w), z = z(u, v, w), причём x(u, v, w), y(u, v, w), z(u, v, w) осуществляют взаимно-однозначное отображение области Т пространства Oxyz на область T₁ пространства Ouvw и якобиан преобразования не обращается в нуль в области T₁:

,

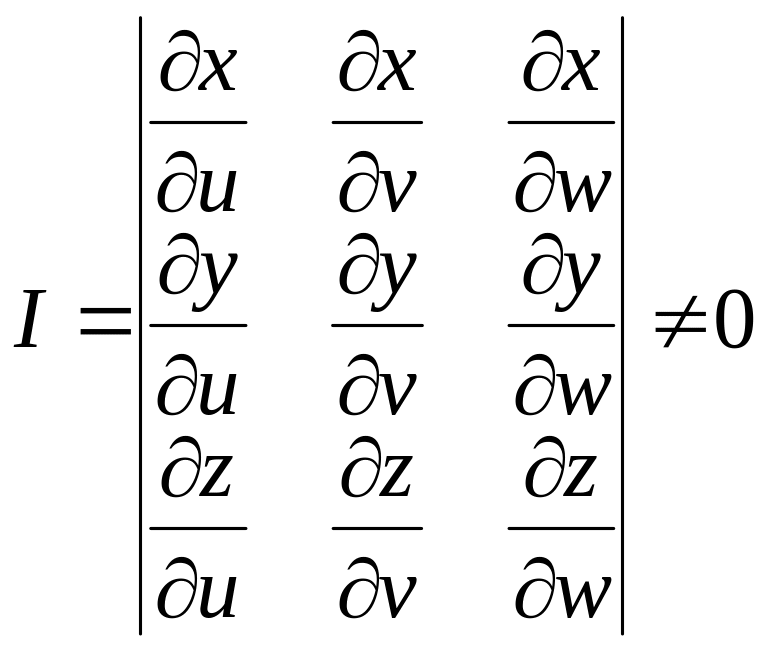то справедлива формула

. (18)

Наиболее употребительными из криволинейных координат являются

цилиндрические координаты: r, φ, z (рис. 6.3): x = rcosφ, y = rsinφ, z = z, якобиан которых I = r,

и сферические координаты: r (длина радиус-вектора), φ (долгота), θ (широта) (рис. 6.4): x = rcosφcosθ, y = rsinφcosθ, z = rsinθ, якобиан которых равен I = r² cosθ.

Рис.6.3 Рис. 6.4

Формула (18) принимает соответственно вид

(19)

или

.,

Применение тройных интегралов в задачах геометрии и механики

1. Объем V пространственной области Т равен

.

2. Масса тела с переменной плотностью γ(x, y, z), занимающего область Т:

.

2. Статические моменты тела относительно координатных плоскостей:

,

,

.

2. Координаты центра масс тела:

, , .

2. Моменты инерции тела относительно осей координат:

,

,

.

Если тело однородно, то в приведённых выше формулах следует положить γ(x, y, z) =1.

Векторное поле

Векторным полем называется часть пространства, каждой точке которого поставлен в соответствие вектор :

.

Векторными линиями векторного поля называются такие линии, которые в каждой своей точке М имеют направление . Они определяются системой дифференциальных уравнений

.

Если поле а – силовое поле, то работа А поля при перемещении материальной точки по дуге L равна

.

Циркуляция векторного поля по замкнутому контуру С в выбранном направлении равна

.

Потоком векторного поля через поверхность S в сторону, определяемую единичным вектором нормали к поверхности S, называется интеграл

.

Дивергенцией векторного поля в точке M₀ называется скалярная величина , равная отнесённому к единице объёма потоку вектора через поверхность бесконечно малого объёма, окружающего данную точку:

.

В декартовых координатах дивергенция вычисляется по формуле

.

Ротором (вихрем) векторного поля в точке M₀ называется вектор, проекция которого на любое направление определяется равенством

,

где S – площадь площадки, перпендикулярной , ограниченной замкнутым контуром C. Контур С пробегается против часовой стрелки, если смотреть на него из конца вектора .

В декартовых координатах:

.

Формула Стокса. Циркуляция векторного поля по замкнутому контуру С равна потоку его ротора через произвольную поверхность S, «натянутую» на контур С:

.

где направление нормали к поверхности S согласовано с направлением обхода контура С.

Вектор , являющийся градиентом некоторого скалярного поля φ называется потенциальным вектором, а поле вектора называется потенциальным полем, скалярная функция φ называется потенциалом векторного поля.

Для потенциальности поля , заданного в односвязной области, необходимо и достаточно, чтобы оно было безвихревым, т.е. чтобы . В этом случае существует потенциал φ, определяемый как решение уравнения

.

С точностью до постоянной он находится по формуле

,

где интеграл берётся по любому пути, исходящему из некоторой фиксированной точки M₀, где поле существует. Обычно в качестве пути выбирают ломаную, звенья которой параллельны координатным осям, например, ломаную M₀M₁M₂M (рис. 6.5), а φ(M₀) полагают равной С (С=const). Тогда

.

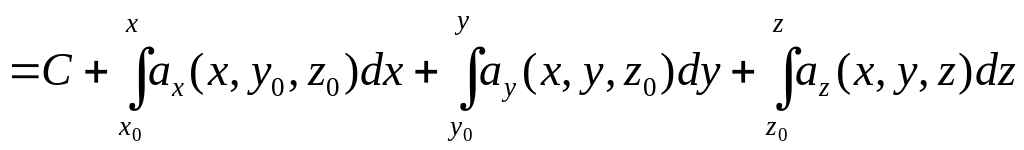Рис. 6.5