Лабораторная работа № 6

Цель работы: лабораторной работы – ознакомить студентов с возможностями использования пакета Mathcad для решения кратных интегралов, привить навыки работы с компьютером в процессе изучения дисциплины «Компьютерные исчисления», навыки самостоятельной работы с современными математическими программами.

Указания к выполнению лабораторной работы:

Подобно тому, как задача о нахождении площади криволинейной трапеции, а также ряд задач механики и в, частности, задача о нахождении работы, совершаемой переменной силой по перемещению материальной точки вдоль отрезка прямой, привели к понятию определённого интеграла, так и более сложные задачи геометрии и физики (нахождение объёма тела, площади криволинейной поверхности, массы тела, статических моментов и моментов инерции тел и др.) приводят к понятию кратных интегралов.

Вычисления двойных и тройных интегралов вызывают некоторые трудности у студентов (как правило, расстановка пределов интегрирования в повторных интегралах). Использование компьютерной техники, программного продукта Mathcad позволяет производить достаточно громоздкие вычисления, связанные с непосредственным вычислением интегралов и строить графики функций, ограничивающих область интегрирования, что существенно повышает наглядность и способствует более глубокому пониманию изучаемых теоретических положений. В пятой и шестой лабораторных работах рассмотрены элементы теории поля, т. е.

решается ряд задач, связанных со скалярными и векторными полями.

Отчёт по лабораторной работе должен включать выполнение индивидуального задания и ответы на вопросы.

Задание 1. Вычислить двойной интеграл по указанной области G.

Задание 2: Найти площадь фигуры, ограниченной данными линиями.

Задание 3. Вычислить координаты центра тяжести пластины.

Задание 4. Тело V задано ограничивающими его поверхностями, - плотность. Найти объем тела.

Задание 5. Покажите, что поле является потенциальным, и найдите потенциал этого поля.

Теоретические положения Двойной интеграл

Пусть функция f(x, y) = f(P) определена и непрерывна на замкнутой ограниченной области G плоскости Oxy, – некоторое разбиение области на элементарные подобласти , площади которых также обозначим через , а диаметры – через d_k. Зафиксируем точки P_k  ,k=1, 2, …n. Выражение

называется интегральной суммой для функции f(P) по области G.

Определение. Если существует предел последовательности интегральных сумм S_n при (при этом n ) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти , ни от выбора точек P_k  .

.

Таким образом,

.

Для двойного интеграла справедливы свойства линейности и аддитивности:

а) линейность:

;

б) аддитивность: если G = G₁+G₂, то

.

Вычисление двойного интеграла сводится к вычислению повторных интегралов следующим образом. Пусть область G (рис. 6.1) ограничена кривыми , , x=a, x=b причём всюду на [a, b] функции и непрерывны и . Тогда

,

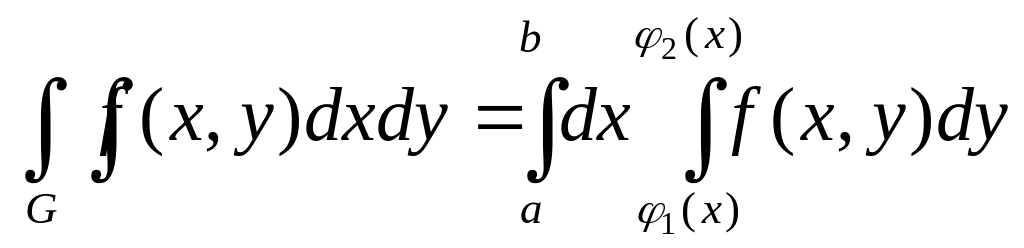причём сначала вычисляется внутренний интеграл по переменной y (x считается постоянной), потом полученный результат интегрируется по x. Интегралы такого вида называются повторными. Если кривая (или кривая ) в промежутке задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.

Рис.6.1 Рис. 6.2

Аналогично, можно построить второй повторный интеграл. Если область G ограничена кривыми , , y=c, y=d, причём всюду на [c, d] функции и непрерывны и (рис. 6.2), то

.
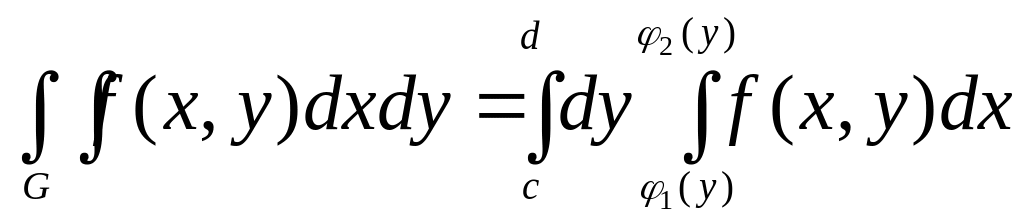