Сравнение различных регрессий. Пошаговый отбор переменных.

На 1-м шаге (k = 1) найдем один наиболее информативную переменную. При k = 1 величина R² совпадает с квадратом обычного (парного) коэффициента корреляции

R²= r² (y, x) ,

из матрицы корреляций находим:

r² (y, x_j) = r² (y, x₄) = (0.577)² = 0.333

Так что в классе однофакторных регрессионных моделей наиболее информативным предиктором (предсказателем) является x₄- количество удобрений. Вычисление скорректированного (adjusted) коэффициента детерминации по (20) дает

R²_adj= 0.296.

2-й шаг (k = 2). Среди всевозможных пар (х₄ , х_j), j = 1, 2, 3, 5, выбирается наиболее информативная (в смысле R² или, что то же самое, в смысле R²_adj) пара:

возврат в окно Selectdep. Andindep.Var. и перебор различных пар; результат:

1. (х₄ , х₁)

(х₄ , х₁) = 0.406,

2. (х₄ , х₂)

(х₄ , х₂) = 0.399

3. (х₄ , х₃)

(х₄ , х₃) = 0.421

4. (х₄ , х₅)

(х₄ , х₅) = 0.255

откуда видно, что наиболее информативной парой является (х₄ , х₃), которая дает

= (х₄ , х_j) = 0.421

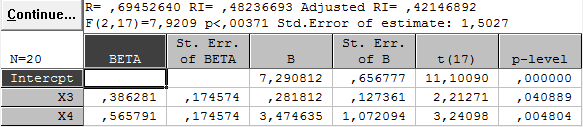
Оценка уравнения регрессии урожайности по факторам х₃и х₄ имеет вид

(х₃, х₄) = 7.29 + 0.28 х₃ + 3.47 х₄ (27)

(0.66) (0.13) (1.07 )

Внизу в скобках указаны стандартные ошибки, взятые из столбца Std. Err. Of B таблицы RegressionResults для варианта независимых переменных (х₃, х₄) Все три коэффициента статистически значимо отличаются от нуля при уровне значимости  = 0.05, что видно из столбца p-level той же таблицы.

3-й шаг (k = 3). Среди всевозможных троек (х₄, х₃,х_j), j = 1, 2, 5, выбираем аналогично наиболее информативную:

1. (х₄, х₃,х₁)

2. (х₄, х₃,х₂)

3. (х₄, х₃,х₅)

(х₄, х₃,х₅) дает = 0.404,

что меньше, чем на предыдущем шаге = 0.421; это означает, что третью переменную в модель включать нецелесообразно, т.к. она не повышает значение(более того, уменьшает). Итак, результатом анализа является (27).

3. Нелинейная зависимость

Связь между признаком x и y может быть нелинейной, например, в виде полинома:

y = P_k (x) + , (28)

где P_k (x) = _о + ₁ x + ...+ _k x^k, k - степень полинома,  - случайная составляющая, М = 0, D = ² .

Для имеющихся данных (x_i ,y_i), i = 1, ..., n, можно записать

y_i = _о + ₁ x_i + ₂ + ...+_k + _i , i =1, ..., n (29)

или, как и (12), в матричной форме:

Y = X  +  , (30)

где .

Имеем задачу (13), и потому все формулы п.2. оказываются справедливыми и в этом случае (28) . Слово “линейный” в названии “линейный регрессионный анализ” означает линейность относительно параметров _j , но не относительно факторов x_j . Широко используется, кроме полиномиальной, например, следующие модели:

1) логарифмическая; если зависимость y = a₀, то после логарифмирования получаем

ln y = ln a_o + a₁ ln x = _о + ₁ ln x;

2) гиперболическая (при обратной зависимости, т.е. при увеличении х признак y уменьшается):

y = _о + ;

3) тригонометрическая:

y = _о + ₁ sinx + ₂ cos x и другие.

Пример. Имеются эмпирические данные о зависимости y - выработки на одного работника доменного производства от x - температуры дутья; данные приведены в табл. 3 в условных единицах.

№	X	Y	№	X	Y
1	1.01	8.8	11	5.80	11.8
2	1.15	9.2	12	6.14	12.2
3	1.91	8.7	13	6.64	13.1
4	2.47	10.2	14	6.85	14.4
5	2.66	9.3	15	8.11	17.5
6	2.74	9.4	16	8.47	18.6
7	2.93	10.7	17	9.09	18.6
8	4.04	8.5	18	9.23	18.0
9	4.50	8.9	19	9.59	23.8
10	4.64	8.0	20	9.96	18.4

Сначала оценим имеющиеся данные визуально, с помощью процедуры Scatterplot(диаграмма рассеяния). Видим, что зависимость, возможно, нелинейная.

Построим несколько регрессий.

1. Регрессия первой степени: y = _о + ₁ x; получим (в скобках указаны стандартные ошибки оценок):

y = 5.37 + 1.40 x

(0.98) (0.16)

= 0.798, s = 2.09.

2. Регрессия второй степени: y = _о + ₁ x + ₂ x² ; получим:

y = 9.95 - 0.90 x + 0.21 x², (31)

(1.33) (0.57) (0.05)

= 0.890, s = 1.53,

коэффициент ₁ = -0.88 незначимо отличается от 0. Эта регрессия лучше предыдущей в смысле иs. Однако, возможно, регрессия третьей степени окажется лучше?

3. Построим регрессию третьей степени: y = _о + ₁ x + ₂ x² + ₃ x³; получим:

y = 11.6 - 2.35 х + 0.53 х² - 0.02 х³

(2.33) (1.74) (0.36) (0.02)

= 0.890,s = 1.53,

незначимо отличаются от 0. Поскольку степень увеличилась без увеличения, от регрессии третьей степени отказываемся в пользу (31) второй степени. Однако, гипотеза о нулевом значении ₁ в (31) не отклоняется (p-level = 0.1), и потому построим

4. регрессию y = _о + ₂ x² без линейного члена ; получим

y = 8.02 + 0.13 x² (32)

(0.54) (0.01)

= 0.881,s = 1.6,

Сравнивая ее по иs с (31) , отдаем предпочтение (31), поскольку ошибка прогноза s меньше.