1.2 Определение длины эквивалентного и критического пролетов и установление исходного расчетного режима

Длину пролета контактной сети рассчитывают, так чтобы отклонения контактного провода от оси токоприемника под действием ветра не превышало норму.

Из теории механического расчет цепной подвески известно, что для определения состояния несущего троса цепной подвески значения натяжения при любой температуре и любой нагрузки нужно знать исходно состояние, т.е температуру нагрузки, соответствующие этим нагрузкам.

По сколько первоначально из всех возможных натяжение несущего троса известно только его максимальное натяжение, необходимо устанавливать, при каком из расчетных режимов для заданного типа подвески и заданных климатических условий в несущем тросе создается наибольшее натяжение; принять этот режим за исходный и рассчитать нагрузку и температуру в этом режиме. Исходный режим определяется из неравенства:

l_кр>l_э – режим минимальная температура;

l_кр<l_э – режим гололеда с ветром.

Расчет длины критического пролета.

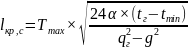, (12)

, (13)

где – натяжение несущего троса контактной подвески;

– величина разрушающей нагрузки при растяжении проводов, кН;

– коэффициент запаса прочности;

– длина критического пролёта, м;

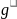, – значения результирующих нагрузок на несущий трос или провод соответственно при режиме гололёда с ветром и при режиме минимальной температуры;

, – температура воздуха соответственно при режиме гололёда с ветром и минимальная;

– характеристика температурного удлинения рассчитываемого несущего троса заданной подвески.

Определение длины эквивалентного пролёта

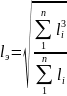, (14)

где – длина пролёта с номером i;

n –число пролётов в анкерном участке.

Расчеты произведены в программе SMath Studio предназначенная для произведения математических расчетов и построения графиков функции. Результаты расчетов приведены в Приложении А.

Поскольку оказалось, что значение критического пролета главного и бокового пути больше эквивалентного, а именно l_э=52,44м<l_кр=150,66м и l_э=52,44м<l_кр=134 м, исходный расчетный (наиболее тяжелый) режим – минимальная температура. Иными словами, натяжение в несущим тросе достигает наибольшего значения, равного Тдоп=20 кН и Тдоп=16кН, в расчетном режиме минимальной температуры. Значит для заданных условий расчета режим минимальной температуры – исходный расчетный режим.

1.3 Определение значений натяжений несущего троса в зависимости от температуры. Построение монтажной кривой Тх(tx)

Расчет зависимости натяжения нагруженного несущего троса от температуры.

Находим постоянные для данного расчета коэффициенты А,В,С

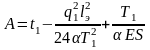, (15)

где Т₁=Т_доп;

t₁=t_min;q₁=g – если расчетный режим – минимальная температура;

t₁=t_Г=-5С˚;q₁=q_ТГ – если расчетный режим – гололеда с ветром;

t₁=t_v=+5C˚; q₁=q_TV – если расчетный режим – максимального ветра;

24α – характеристика температурного удлинения рассчитываемого несущего троса заданной подвески;

l_э – экивалетная длина пролета, м.

, (16)

q_x= g, (17)

, (18)

. (19)

Значение T_vmax и T_г определяем методом подбора по уравнению состояния несущего троса полукомпенсированной контактной подвески.

Температура бес провесного положения контактных проводов

, (20)

где t^/ -величина зависящая от типа и числа контактных проводов.

Расчеты произведены в программе SMath Studio предназначенная для произведения математических расчетов и построения графиков функции. Результаты расчетов приведены в Приложении А. Все полученные результаты расчетов сводится в таблицу 2.

Таблица 2 – Расчет натяжений несущих тросов главного и бокового путей

Главный путь
tx,C˚	-30	-12,5	-5	5	35
Tx,H	20000	16450	15045	13315	9340
Второстепенный путь
tx,C˚	-30	-12,5	-5	5	35
Tx,H	16000	13908	13051	11957	9112

По результатам расчетов приведенных в таблице 2 строим монтажные кривые рисунок 1,2.

Рисунок 1 Монтажная кривая натяжения нагруженного контактным проводом несущего троса главного пути

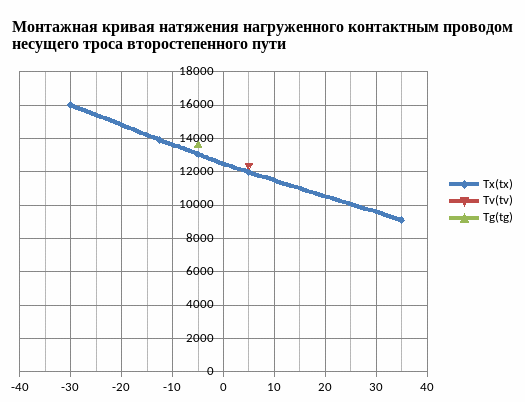
Рисунок 2 Монтажная кривая натяжения нагруженного контактным проводом несущего троса второстепенного пути