4. Достаточные статистики. Критерий факторизации.

Определение 3.11.

Статистика называется достаточной для параметра , если условная плотность вероятности (или условная вероятность в дискретном случае) случайного вектора при условии не зависит от параметра .

Теорема 3.12. (критерий факторизации)

Пусть – наблюдение и – функция правдоподобия вектора . Статистика является достаточной для параметра тогда и только тогда, когда функция правдоподобия имеет вид:

,

где и некоторые функции.

Доказательство:

Рассмотрим доказательство для только для случая, когда все случайные величины ( ) дискретны.

1) Пусть статистика является достаточной для параметра , покажем, что:

.

Функция правдоподобия равна вероятности события :

.

Рассмотрим событие . Легко видеть, что если при некотором выполняются равенства , ..., , то при этом же выполняется равенство , поэтому, очевидно:

откуда следует, что совместное наступление событий и есть событие :

то есть,

.

Отсюда следует равенство для вероятностей событий:

Вероятность справа представим по формуле умножения как произведение условной и безусловной вероятностей:

Условная вероятность, есть условное распределение вектора при условии :

.

Поскольку статистика является достаточной для параметра , то функция не зависит от параметра и может зависеть только от , ..., :

.

Безусловная вероятность очевидно зависит от величины и, возможно, от параметра :

.

Таким образом, для функции правдоподобия получим:

.

2) Пусть имеет место разложение , покажем, что в этом случае статистика достаточна для параметра , то есть условная вероятность не зависит от параметра . По определению условной вероятности:

Если , то вероятность, стоящая в числителе равна нулю независимо от значения параметра . В точке :

.

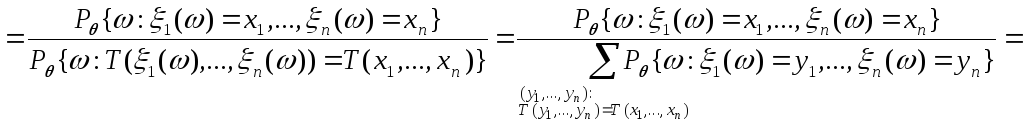
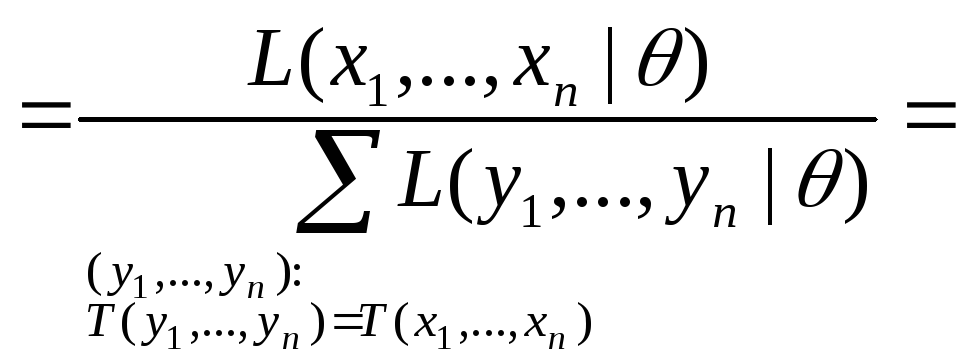
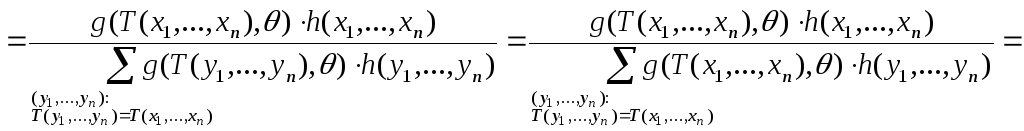
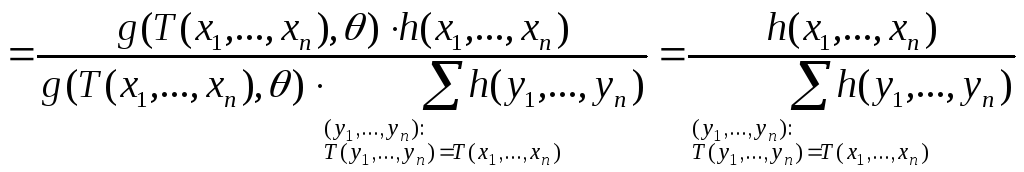Таким образом,

.

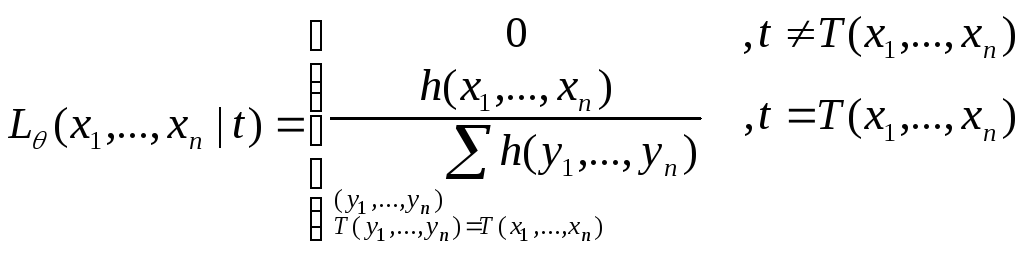Выражение, стоящее справа, очевидно, не зависит от параметра , поэтому условная вероятность не зависит от параметра , и следовательно статистика достаточна для параметра .

Теорема доказана.

Следствие

Пусть выполнены условия теоремы 3.4 и – эффективная оценка, тогда – статистика достаточная для параметра .

Действительно, при выполнении условий теоремы 3.4 согласно утверждению 3.10 имеет место следующая факторизация функции правдоподобия:

.

Положим, и , тогда:

,

и по теореме 3.12 статистика является достаточной для параметра .

Таким образом, при выполнении некоторых условий эффективная оценка является достаточной статистикой. К сожалению, обратное не всегда верно: достаточная статистика не обязательно является эффективной оценкой.

Следствие

Пусть – статистика, достаточная для параметра и – статистика, через которую можно выразить статистику , то есть,

,

тогда статистика тоже достаточна для параметра .

Действительно, если – статистика, достаточная для параметра , то по теореме 3.12 для функции правдоподобия получим факторизацию:

,

подставляя сюда выражение статистики , через статистику ,

,

получим факторизацию:

,

откуда по теореме 3.12 (в обратную сторону) статистика является достаточной для параметра .

Теорема 3.13 (Блекуэлл)

Пусть – несмещенная оценка , – статистика, достаточная для параметра и случайная величина является условным математическим ожиданием величины при условии :

,

тогда

1) случайная величина является статистикой;

2) ;

3) .

Доказательство:

1) Заметим, что условная случайная величина:

(3.6)

где условное распределение случайного вектора при условии . Поскольку является статистикой достаточной для параметра , то по определению, условная плотность от параметра не зависит. Таким образом, справа в (3.6) под интегралом расположены функции, которые от параметра не зависят, и следовательно интеграл является функцией только , поэтому случайная величина , является статистикой, поскольку зависит только от наблюдения :

.

2) Вычислим математическое ожидание , воспользовавшись свойством условного математического ожидания:

,

поскольку является несмещенной оценкой .

3) Представим дисперсию с помощью условного математического ожидания и условной дисперсии:

.

Во втором слагаемом справа , поэтому:

,

поскольку условная дисперсия неотрицательна случайная величина, , то и математическое ожидание от неотрицательной величины условной дисперсии неотрицательно, :

.

Теорема доказана.

Утверждение 3.14.

Пусть – оптимальная оценка в классе несмещенных оценок (то есть – эффективная оценка ) и – статистика достаточная для параметра , тогда статистика является функцией :

,

где некоторая функция.

Доказательство:

Определим статистику следующим образом:

,

тогда по теореме 3.13 оценка является несмещенной:

,

и кроме того,

.

Оценка является оптимальной в классе несмещенных оценок , и следовательно среди всех несмещенных оценок имеет наименьшую дисперсию, поэтому для всякой несмещенной оценки, в том числе и для :

Из двух неравенств следует, что

.

Таким образом, статистика также является оптимальной оценкой в классе несмещенных оценок , но несмещенная оптимальная оценка единственна (утверждение 1.12), отсюда статистики и совпадают:

.

Статистика является условным математическим ожиданием, и следовательно является функцией , поэтому:

.

Утверждение доказано.

Достаточные статистики кроме ранее отмеченных свойств имеют одно примечательное свойство, следующее непосредственно из определения. Поскольку условная плотность вероятности (или вероятность в дискретном случае) случайного вектора при известном значении достаточной статистики не зависит от параметра , то «количество информации» о параметре , содержащееся в наблюдении , равно «количеству информации» о параметре , содержащейся в достаточной статистике . Указанное свойство позволяет не хранить реализацию наблюдения , а вычислять значение достаточной статистики и хранить вычисленное значение. В случае, когда размерность достаточной статистики меньше количества случайных величин наблюдения , указанный подход позволяет «сжимать данные» без потери информации о параметре в статистическом смысле.

Более того, для каждой статистической процедуры , основанной на использовании наблюдения , может быть построена «эквивалентная» процедура , основанная на достаточной статистике . Действительно, пусть в результате некоторого эксперимента случайный вектор приобрел конкретное числовое значение . Вычислим значение достаточной статистики и вектор отбросим (он более не требуется). Далее, поскольку условная плотность вероятности случайного вектора не зависит от неизвестного параметра, то может быть построен генератор случайного вектора , на вход которого подается значение достаточной статистики . На выходе генератора будет получен числовой вектор , вообще говоря, отличный от исходного вектора . Однако вектор также будет реализацией вектора , поэтому можно считать вектор «равноценным» вектору . Затем, статистическая процедура применяется уже к вектору .

38