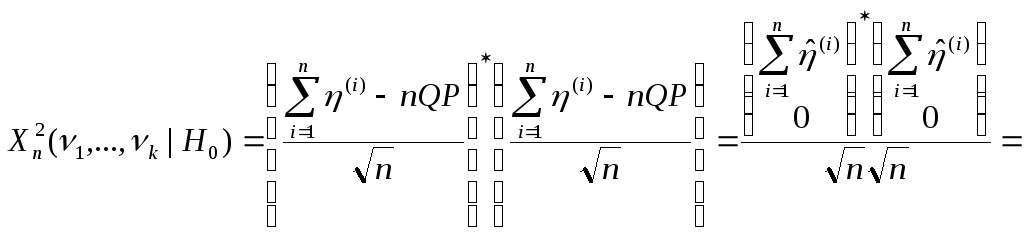Добавил:

Tushkan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Теория вероятностей и математическая статистика

Файл:

Лекции / Tema_6.doc

Скачиваний:

Добавлен:

28.06.2014

Размер:

2 Мб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

2. Критерий хи-квадрат проверки простой гипотезы о вероятностях.

Представим себе, что проводится серия независимых испытаний, в каждом из которых происходит в точности одно из событий , , …, (события образуют полную группу событий), имеющих неизвестные вероятности , , …, ( ). По результатам серии фиксируется количество наступлений события , количество наступлений , и так далее до , так что наблюдение представляет собой вектор , имеющий полиномиальное распределение, которое будем обозначать :

(Заметим, что отсюда в частности следует, что каждая случайная величина имеет распределение Бернулли, действительно, для получим ( ):

Очевидно, то же самое может быть проделано и для любого , поэтому ).

Основная гипотеза заключается в том, что неизвестные вероятности равны заданным вероятностям ( ):

: , , …, .

Требуется построить статистический критерий проверки гипотезы .

Для решения сформулированной задачи используется критерий хи-квадрат со статистикой критерия следующего вида:

Статистика отражает «суммарное» отклонение наблюдаемых количеств наступлений событий , от ожидаемых средних количеств наступлений событий – , причем каждое отклонение входит в сумму с «весом» , учитывающим величину гипотетической вероятности .

Оказывается, что в том случае, когда гипотеза не верна, статистика с большой вероятностью принимает «большие» значения (утверждение 6.14), поэтому гипотезу следует отклонять, если значение статистики оказалось «большое», то есть в качестве критической области гипотезы следует брать области вида:

где – некоторый порог, выбираемый из условия заранее заданного уровня значимости . По определению уровень значимости есть вероятность:

откуда следует, что в качестве порога следует брать квантиль уровня того распределения статистики , которое определяется гипотезой . Точное выражение для функции распределения найти затруднительно, однако, можно показать (теорема 6.15), что если гипотеза верна, то функция распределения при возрастании стремится к функции распределения хи-квадрат с степенью свободы, то есть при больших :

Таким образом, проверка гипотезы сводится к следующей последовательности действий:

1) по заданному уровню значимости определяется квантиль уровня распределения ;

2) по реализации наблюдения (числовым данным, полученным в результате проведения эксперимента) вычисляется значение статистики ;

3) если , тогда гипотеза отклоняется, если , тогда гипотеза принимается.

Перейдем к доказательству основных фактов, использованных при формулировке критерия. Прежде всего, покажем, что в случае, когда гипотеза не верна, значения статистики неограниченно возрастают с ростом .

Утверждение 6.14.

Пусть наблюдение имеет полиномиальное распределение , и основная гипотеза заключается в том, что ( ).

Если гипотеза не верна, тогда последовательность (по ) случайных величин не ограничена по вероятности, то есть:

, при .

Доказательство:

Пусть и произвольно выбранные числа, покажем, что найдется такое, что для всех :

это и будет означать, что .

По условию утверждения гипотеза не верна, поэтому найдутся такие индексы , при которых , пусть – один из таких индексов, то есть .

Поскольку (следует из того, что наблюдение имеет полиномиальное распределение ), то в соответствии с теоремой Бернулли:

, при ,

отсюда следует, что для выбранного ранее и для ( поскольку ) найдется номер такой, что для всех :

Отсюда следует, что

Если , тогда:

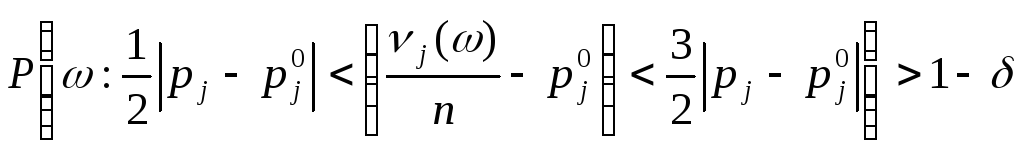В том и другом случаях,

Из вложенности событий:

следует неравенство для вероятностей событий:

Пусть есть событие:

тогда , и для произвольного :

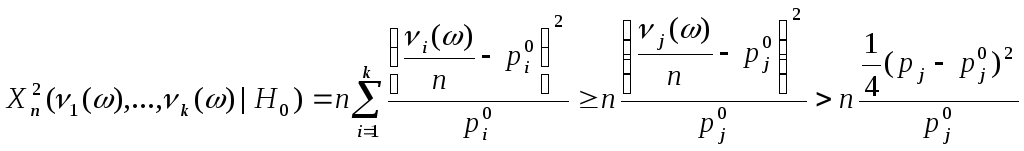Пусть , тогда для :

Отсюда следует, что при :

тогда

Таким образом, для произвольных и найден способ определения числа такого, что для всех :

Утверждение доказано.

В силу утверждения 6.14 статистика отвечает условию а) определения статистики критерия 6.5: в случае если гипотеза не верна, статистика с большой вероятностью примет «большое» значение, которое укажет на «большое» расхождение между наблюдаемыми величинами и ожидаемыми значениями.

Для того, чтобы статистика отвечала и пункту б) определения статистики критерия и могла быть использована в статистическом критерии, остается лишь найти способ вычисления (хотя бы приближенного) значений функции распределения статистики . Оказывается, что в случае если гипотеза верна (то есть , ) распределение статистики с ростом стремится к распределению .

Теорема 6.14. (Пирсон)

Пусть наблюдение имеет полиномиальное распределение ( ). Если верна гипотеза :

: , ,

тогда распределение статистики стремится к распределению хи-квадрат с степенью свободы:

, при .

Доказательство:

Преобразуем статистику следующим образом:

где вектор-столбец :

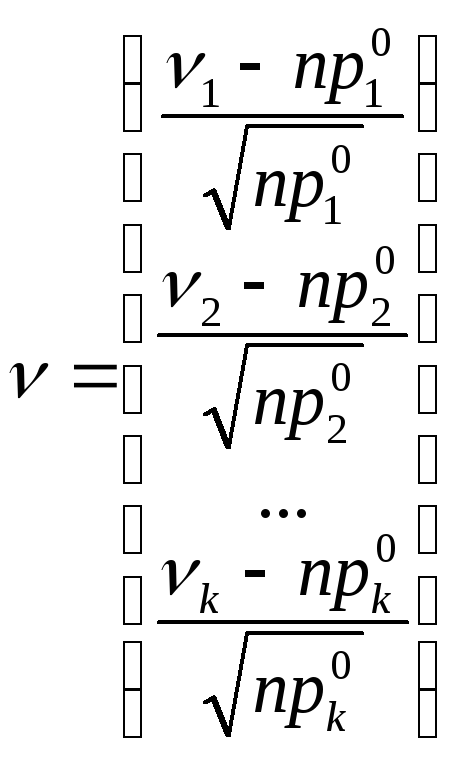и – транспонированный вектор .

Представим, что исходным наблюдением является не вектор , а выборка объема , в которой каждая случайная величина отражает исход -го испытания и принимает значения 1, 2, …, в зависимости от того, событие с каким номером наступило в -ом испытании:

Пусть – бинарная случайная величина:

Заметим, что математическое ожидание , и кроме того, легко видеть, что , тогда:

где – вектор-столбец случайных величин и – вектор столбец:

, .

Таким образом, статистика :

Поскольку все случайные величины выборки имеют одинаковое распределение, то все векторы ( ) имеют одинаковые моменты. Вычислим математическое ожидание :

Поскольку по условию теоремы гипотеза считается верной, то , тогда:

Вычислим дисперсионную матрицу :

Если , то , поскольку случайная величина не может принимать два различных значения и одновременно, и следовательно . Если , тогда , тогда:

Таким образом,

Поскольку по условию теоремы гипотеза считается верной, то , тогда:

Отсюда следует, что дисперсионную матрицу можно представить в виде:

где – единичная матрица порядка , – транспонированный вектор .

Как и ожидалось, дисперсионная матрица является вырожденной. Действительно, что если дисперсионную матрицу умножить на вектор , то получится нулевой вектор :

Легко видеть, что

тогда

Если бы матрица была невырожденной, то равенство с некоторым вектором выполнялось бы только в случае , то есть не могло бы существовать ни одного ненулевого вектора , при котором выполнялось бы равенство . Однако, найден ненулевой вектор такой, что , тогда матрица обязательно вырождена. Поскольку все векторы имеют вырожденную дисперсионную матрицу, то к сумме не применима центральная предельная теорема для многомерного случая.

Преобразуем векторы в векторы с помощью ортогонального преобразования с матрицей ( – транспонированная матрица ):

тогда статистика преобразуется к следующему виду:

Поскольку векторы имеют одинаковые математические ожидания и дисперсионные матрицы, то векторы имеют также одинаковые математические ожидания и дисперсионные матрицы. Математическое ожидание :

(6.1)

Дисперсионная матрица :

Дисперсионная матрица оказывается «почти единичной». Представим, что в матрице последняя строка совпадает с транспонированными вектором-столбцом :

где – матрица порядка . Поскольку – ортогональная матрица, то её строки являются взаимно ортогональными векторами, отсюда следует, что строки матрицы являются взаимно ортогональными векторами, которые к тому же ортогональны и вектору , тогда:

(6.2)

где – нулевой вектор-столбец порядка , и следовательно:

то есть – матрица все элементы, которой равны нулю, кроме элемента в -ой строке и -ом столбце, который равен 1. Таким образом, дисперсионная матрица :

(6.3)

где единичная матрица порядка .

Заметим, что

поскольку,

в силу того, что случайная величина принимает одно из целых значений от до , так что в сумме обязательно в точности одно слагаемое будет равно 1 и остальные будут равны 0.

Пусть , тогда , причем из (6.1) и (6.2) следует:

(6.4)

и в силу (6.3),

(6.5)

Заметим, что

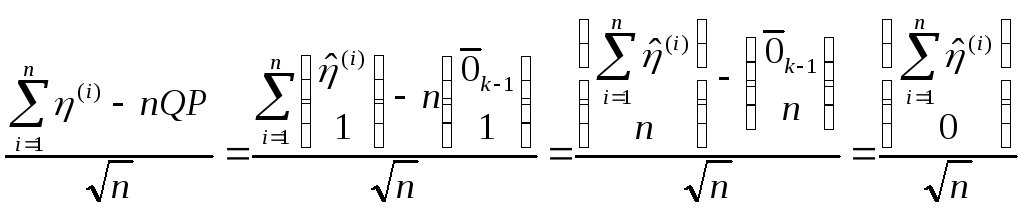тогда статистика :

(6.6)

Векторы имеют одинаковые распределения (поскольку векторы и следовательно имеют одинаковые распределения), математические ожидание (6.4) и невырожденные дисперсионные матрицы (6.5), поэтому к последовательности случайных величин применима центральная предельная теорема для многомерного случая, согласно которой нормированная сумма имеет асимптотически многомерное нормальное распределение :

, при .

Пусть вектор-столбец случайных величин , поскольку распределение вектора стремиться к распределению случайной величины , то распределение случайной величины стремится к распределению случайной величины . Таким образом, из (6.6) распределение статистики стремится к распределению суммы квадратов :

Взятые по отдельности случайные величины имеют нормальное распределение с нулевым математическим ожиданием и единичной дисперсией, и кроме того независимы поскольку являются некоррелированными (дисперсионная матрица является единичной, так что все ковариации при ) нормальными случайными величинами. Отсюда следует, что случайная величина имеет распределение , тогда и статистика при имеет распределение :

, при .

Теорема доказана.

Можно показать, что критерий хи-квадрат является состоятельным: в данном случае наблюдение имеет полиномиальное распределение , полностью определяемое вектором вероятностей и числом .

Утверждение 6.16.

Пусть наблюдение имеет полиномиальное распределение и основная гипотеза заключается в том, что ( ), статистика критерия имеет вид:

и критическая область , тогда при всяком альтернативном распределении значение функции мощности :

стремится к 1 при :

Без доказательства.

Ранее было показано, что если гипотеза верна, то распределение статистики при увеличении стремится к распределению , можно также установить, что если гипотеза не верна, то распределение статистики при увеличении стремится к нецентральному распределению хи-квадрат .

Случайная величина имеет нецентральное распределение , если:

где – совместно независимые случайные величины, и , при этом плотность вероятности случайной величины зависит только от величины , но не по отдельности от , …, .

Утверждение 6.17.

Пусть наблюдение имеет полиномиальное распределение ( ) и основная гипотеза заключается в том, что ( ).

Если гипотеза не верна, тогда распределение статистики :

стремится при к нецентральному распределению .

Без доказательства.

Условия применимости на практике.

Поскольку известно только предельное (при ) распределение статистики (теорема 6.15), то для конечного использование распределения в качестве распределения является приближенным. Замечено, что «хорошее» приближение достигается в тех случаях, когда все произведения ( ),

Проверка гипотезы о распределении полностью известном.

Рассмотрим следующую задачу проверки гипотезы: пусть – выборка из неизвестного распределения и основная гипотеза заключается в том, что , где – известная функция распределения. Требуется предложить критерий проверки гипотезы .

Воспользоваться критерием хи-квадрат для решения непосредственно поставленной задачи не возможно, тем не менее, имеется возможность сформулировать «близкую» к поставленной задачу, для решения которой использовать критерий хи-квадрат.

Пусть некоторые числа, рассмотрим разбиение числовой оси на интервалы и полуинтервалы:

…,

Зафиксируем некоторый номер и определим события,

…,

Легко видеть, что события , , …, вообще говоря при всех одинаковы, поскольку все случайные величины выборки одинаковы (имеют одну и ту же функцию распределения ), и кроме того образуют полную группу событий, поскольку несовместны и их объединение есть множество всех элементарных событий. Определим вероятности , , …, событий , , …, :

…,

Рисунок 6.3. Разбиение и вероятности.

Из исходного наблюдения – выборки – сформируем вектор по правилу:

то есть – случайное количество величин выборки попавших в интервал (полуинтервал) .

В качестве основной гипотезы рассмотрим «расширенную» гипотезу :

, ,

…,

(6.7)

Теперь для проверки «расширенной» гипотезы может быть использован критерий хи-квадрат, рассмотренный выше.

Из (6.7) следует, что гипотеза заключается в том, что:

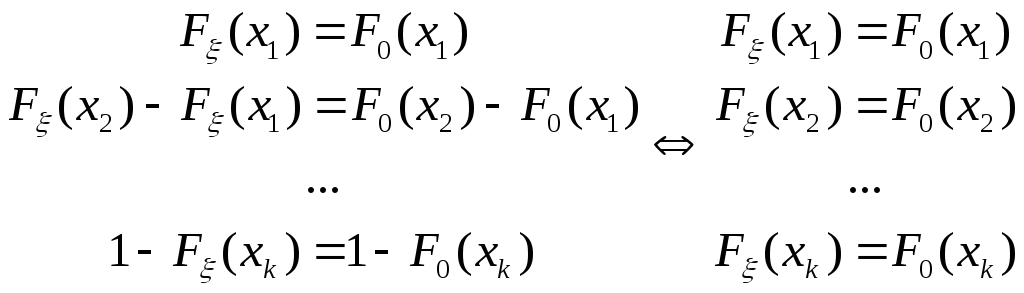
Таким образом, «расширенная» гипотеза утверждает, что только для точек , а гипотеза утверждает, что для всех , поэтому и , вообще говоря, различные гипотезы. Фактически, утверждает, что истинное распределение принадлежит некоторому множеству :