3. Точечное оценивание.

Во многих задачах математической статистики требуется построить оценку некоторой неизвестной величины, в качестве которой может выступать, например, вероятность некоторого события, начальный или центральный момент некоторой случайной величины, параметр некоторого распределения. Для построения оценок требуется статистическая информация, которая поступает в виде наблюдения, поэтому неформально построение оценки сводится к разработке способа (метода) обработки наблюдения, что формально соответствует понятию статистики.

Определение 1.8.

Статистикойназывается функция наблюдения.

Общий случай постановки задачи точечного оценивания может оказаться сложным для восприятия (общий случай рассмотрен, например, в монографии [1]), поэтому рассмотрим частный, простой случай, в котором наблюдение является выборкой.

Пусть является выборкой из распределения, где– неизвестный параметр (в общем случае вектор неизвестных параметров) из некоторого допустимого множества параметров, и требуется построить оценку неизвестной величины, зависящей от параметра. Например, в качестве неизвестной величиныможет выступать непосредственно сам параметр,, вероятностьпри некотором фиксированном,, или математическое ожидание,

.

Предположим, что для оценки неизвестной величины некоторым образом была построена статистика, являющаяся в данном случае функцией выборки(заметим, что оценкаявляется случайной величиной, как функция случайных величин, …,). Для исследования «качества» оценкиопределяют ряд свойств, среди которых особо выделяют свойства несмещенности, состоятельности и оптимальности.

Определение 1.9.

Оценка являетсянесмещенной оценкой, если

:,

где ) ифункция распределения выборки.

Фактически, свойство несмещенности означает, что каково бы ни было значение параметра , оценка«в среднем» окажется близкой к неизвестной величине.

Определение 1.10.

Оценка называетсясостоятельной, если при каждом:

при.

Из свойства состоятельности, согласно определению сходимости по вероятности (приложение 1), следует, что для всякихиможно найтитакое, что при каждом:

.

Фактически это означает, что с увеличением объема выборки вероятность малого отклонения оценкиот значенияоказывается близкой к 1, то есть при большихс большой вероятностью (с вероятностью близкой к 1), значениеокажется в-окрестности величины.

Свойство состоятельности является обязательным свойством, оценки, не обладающие состоятельностью, не рассматриваются и не используются. Свойство несмещенности является желательным, более того, в некоторых случаях смещенные оценки оказываются «лучше» несмещенных, поэтому предпочтение отдают смещенным оценкам несмотря на отсутствие у них свойства несмещенности.

В некоторых случаях у оценки существует второй центральный момент (дисперсия), который в общем случае зависит от значения параметра,

.

По величине дисперсии можно судить о мере «разброса» оценки: оценки с большим «разбросом» могут с большей вероятностью принимать значения далекие от оцениваемой величины, чем оценки с малым «разбросом». Кроме того, оценка с малым «разбросом» оказывается «сосредоточенной» вокруг математического ожидания, которое в случае дополнительного свойства несмещенности совпадает с оцениваемой величиной, так что оценка фактически оказывается «сосредоточенной» вокруг величины. Отсюда следует, что предпочтение следует отдавать оценкам с малым «разбросом» (с малой величиной дисперсии).

Используя величины дисперсий оценок, можно сформулировать критерий наименьшей дисперсии сравнения оценок – «из двух оценок лучше та оценка, у которой дисперсия меньше».

Предположим, что есть класс несмещенных оценок величиныс ограниченной дисперсией:

:,.

Пусть идве различных оценки из класса, в общем случае на основе дисперсийине всегда удается указать, какая оценка «лучше», поскольку может оказаться (рисунок 1.2), что при одном значении параметра:

,

а при другом значении параметра наоборот:

.

В этом случае по принятому критерию наименьшей дисперсии невозможно указать, какая оценка лучше.

Рисунок 1.2. Дисперсии оценок.

Тем не менее, в некоторых случаях в классе есть оценка, которая при каждом значении параметраимеет наименьшую дисперсию среди дисперсий оценок класса(рисунок 1.3):

:.

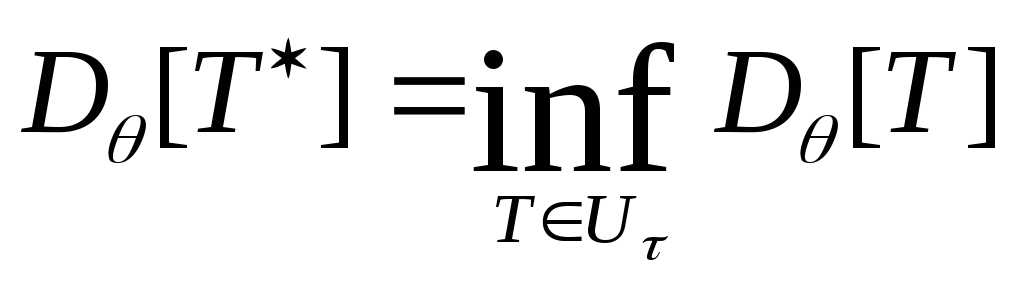В этом случае, оценка , очевидно, является наилучшей в классеи её следует признать оптимальной.

Рисунок 1.3. Дисперсия оптимальной оценки.

Определение 1.11.

Оценка называетсяоптимальной в классе оценок, если

:.

Утверждение 1.12.

Пусть класс несмещенных оценок, если в классесуществует оптимальная оценка, то она единственна.

Доказательство:

Докажем утверждение от противного: пусть оптимальная оценка, предположим, чтодругая оптимальная оценка, которая не совпадает с,.

Образуем оценку следующим образом:

.

Вычислим математическое ожидание , учитывая, чтои, посколькукласс несмещенных оценок:

,

таким образом, оценка также является несмещенной и поэтому.

Вычислим дисперсию :

(1.1)

Согласно свойству ковариации , поэтому:

.

Поскольку иоценки оптимальные, то их дисперсии совпадают, поскольку по определению оптимальной оценки:

,

тогда очевидно,

,

таким образом,

.

С другой стороны, оценка является оптимальной, поэтому по определению оптимальной оценки:

.

Из двух полученных неравенств следует, что:

.

С учетом полученного равенства и равенства из (1.1) получим:

,

(1.2)

По свойству ковариации полученное равенство возможно тогда и только тогда, когда исвязаны линейно:

.

Вычислив математическое ожидание левой и правой частей, получим:

,

,

,

тогда,

,

.

С учетом полученного равенства из (1.2) получим:

,

откуда , то есть:

.

Полученное равенство противоречит исходному предположению о том, что оценкиине совпадают.

Утверждение доказано.

Критерий наименьшей дисперсии не является единственным критерием сравнения оценок, для оценок общего вида, не обязательно обладающих свойством несмещенности, вводится характеристика среднеквадратической ошибки.

Определение 1.13.

Среднеквадратической ошибкойстатистики, оценивающей величину, называется математическое ожидание квадрата отклонения:

.

В случае несмещенной оценки, , среднеквадратическая ошибка становится равной дисперсии, поэтому для несмещенных оценок критерий наименьшей среднеквадратической ошибки совпадает с уже рассмотренным критерием наименьшей дисперсии.

В более общем случае в рассмотрение вводится функция потерь , которая используется при вычислении функции условного риска:

,

где функция распределения выборки. Значения функциииспользуются для сравнения оценок, в частности, если, то функция условного рискаесть среднеквадратическая ошибка.

9