3. Точечное оценивание математического ожидания и дисперсии для функции распределения.

Пусть выборка из распределенияс неизвестным параметром, требуется построить оценки первого начального момента (математического ожидания)и второго центрального момента (дисперсии)(при условии, что указанные моменты конечны):

,

и исследовать свойства построенных оценок.

Для построения оценок воспользуемся определениями моментов, приведенными выше, в которых неизвестную функцию распределения заменим известным «приближением» – эмпирической функцией распределения:

,

.

Поскольку является ступенчатой функцией, с разрывами величиныв точках(), то в результате вычисления интегралов получим следующие статистики:

	(2.2)
	(2.3)

Определение 2.2.

Статистика называетсявыборочным средним.

Определение 2.3.

Статистика называетсявыборочной дисперсией.

Легко видеть, что оценка является несмещенной, действительно:

.

Для доказательства состоятельности оценки может быть использована теорема Хинчина или утверждение 2.1. Заметим, что в случае использования утверждения 2.1 требуется существование дисперсий случайных величин, в то время как теорема Хинчина применима даже в тех случаях, когда у случайных величиндисперсии не существует.

В данном случае величины ,, …,образуют выборку, поэтому они независимы, имеют одинаковую функцию распределения, и, следовательно, одинаковое математическое ожидание, конечность которого гарантируется исходной постановкой рассматриваемой задачи оценки. Таким образом, к совокупности случайных величин, …,приприменима теорема Хинчина, и поскольку статистикаесть в точностиполучим:

, при,

что и означает состоятельность оценки .

Поскольку оценка является несмещенной, то состоятельность оценкиможет быть доказана с использованием утверждения 2.1, при условии, что дисперсия оценкиконечна и стремиться к нулю с ростом. Вычислимнепосредственно из определения статистики:

поскольку величины , …,образуют выборку, то согласно определению выборки они независимы в совокупности и, следовательно, попарно независимы, так что при. При, конечно,, поэтому:

(2.4)

Поскольку предполагается конечной по условию постановки исходной задачи, приведенной в начале пункта, то дисперсияконечна и монотонно стремится к нулю с ростом, поэтому в силу утверждения2.1оценкаявляется состоятельной.

Исследуем свойства оценки , предварительно преобразовав статистикук следующему виду:

.

Вычислим математическое ожидание :

(поскольку , то

)

(дисперсия была вычислена ранее – соотношение 2.2)

Таким образом,

(2.5)

и оценка оказывается смещенной, но смещение легко исправить, в результате приходим к новой оценке:

.

Оценка является несмещенной, действительно,

.

Определение 2.4.

Статистика называетсяисправленной выборочной дисперсией.

Для доказательства состоятельности оценки может быть использована теорема Хинчина и свойства сходимости по вероятности. Ранее было получено выражение для оценкив виде:

К совокупности случайных величин применима теорема Хинчина: величинынезависимы и имеют одинаковую функцию распределения (поскольку величиныобразуют выборку), кроме того, математическое ожидание каждой величиныконечно (по условию постановки исходной задачи, приведенной в начале пункта). Таким образом, по теореме Хинчина:

, при.

Оценка является состоятельной, что по определению означает:

, при

откуда по определению сходимости по вероятности

, при.

Функция возведения в квадрат является непрерывной, и, как и для всякой непрерывной функции, в силу свойства сходимости по вероятности:

, при.

В силу свойства суммы двух пределов по вероятности,

, при,

откуда следует, что

, при,

то есть оценка в соответствии с определением является состоятельной.

Для доказательства состоятельности оценки могут быть использованы свойства сходимости по вероятности или утверждение 2.1.

В соответствии с определением оценки :

,

где оценка состоятельна, то естьпри, и числовая последовательностьстремиться к 1 при. Последнее означает, что для любоговсегда можно найтитакое, что при:

,

отсюда, считая элементы последовательности функциямитождественно равные постоянным, получим:

,

тогда, очевидно, что и для всякого :

.

Таким образом, числовая последовательность сходится по вероятности к 1 при,. Оценка, отсюда по свойству сходимости по вероятности:

, при.

Поскольку статистика является несмещенной оценкой, то для проверки состоятельности статистикиможно воспользоваться утверждением 2.1, для этого покажем, что дисперсия статистикиконечна и стремиться к нулю с ростом,при. При вычислении дисперсиидополнительно потребуется существование четвертого центрального момента:

,

будем считать, что это требование выполнено.

Прежде всего, вычислим дисперсию статистики, которую, как было показано ранее, можно представить в следующем виде:

.

Далее, подставляя выражение для получим:

.

Введем центрированные случайные величины , тогда дляполучим выражение:

Теперь, возводя в квадрат и преобразовывая, получим выражение:

.

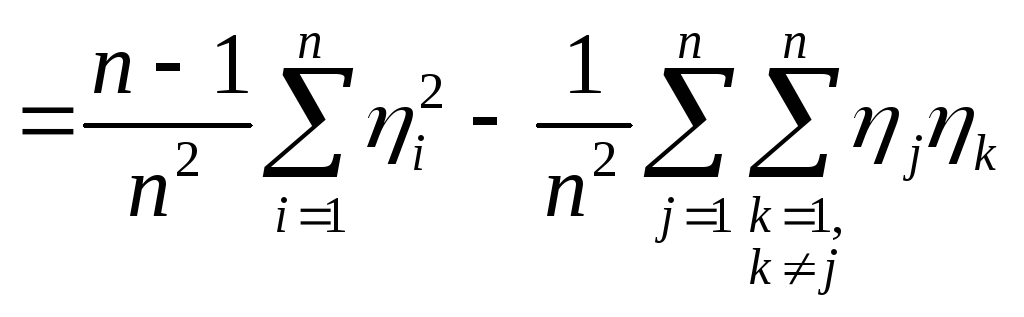Представим дисперсию в виде:

(2.4)

Вычислим :

.

Заметим, что величины () совместно независимы, поскольку независимы величины(), так какобразуют выборку, и кроме того:

.

Рассмотрим слагаемые в сумме, зафиксируем, и рассмотрим все возможные варианты для индексови:

1) ,

а) – невозможно, посколькуи;

а) :

;

2) ,

а) :

;

б) :

.

Таким образом, все слагаемые .

Рассмотрим слагаемые в сумме, зафиксируем индексыи, и рассмотрим все возможные варианты для индексови:

1) :

а) – невозможно, посколькуи;

б) :

;

в) ,:

;

2) :

а) :

;

б) – невозможно, посколькуи;

в) ,:

;

3) и:

а) :

;

б) :

;

в) ,:

;

Заметим, что только в случае 1б) ,и в случае 2а),слагаемоеможет быть отлично от нуля, во всех остальных случаях слагаемое.

Таким образом, для получим выражение:

.

Поскольку , то

Поскольку величины () независимы, то, тогда:

.

Таким образом,

.

Из (2.4) с учетом (2.3) получим выражение для дисперсии:

.

Зная выражение для дисперсии , легко вычислить дисперсиюоценки. Поскольку, то:

.

Поскольку и, то очевиднои, при, откуда в силу утверждения2.3оценкаявляется состоятельной.