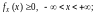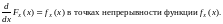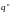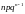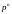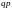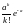(содержание лекций составлено на основе источников, перечисленных в разделе «Литература»)

Лекция 1. Случайные величины. Законы распределения. Скалярные и векторные, дискретные и непрерывные случайные величины. Числовые характеристики случайных величин. Квантиль.

1. Законы распределения и числовые характеристики случайных величин. Случайной величиной X называется действительная функция X = X (ω), определенная на множестве элементарных исходов Ω и такая, что при любом действительном х множество тех ω, для которых X(ω) < х, принадлежит алгебре событий для данного эксперимента.

Случайные величины принято обозначать большими буквами латинского алфавита, а их возможные значения — соответствующими малыми буквами.

Функция F_x (x) действительной переменной х, — ∞ < х < ∞, определяемая формулой

(1.1)

называется функцией распределения случайной величины X. Функция распределения обладает следующими свойствами:

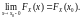
Вероятность попадания случайной величины X на произвольный интервал действительной оси [x₁, x₂) определяется формулой

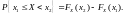(1.2)

Различают дискретные и непрерывные случайные величины (сокращенно ДСВ и НСВ).

Случайная величина X называется дискретной случайной величиной, если множество ее возможных значений {x₁, x_2,……} конечно или счетно.

Пусть Р{Х = х_к} = p_k > 0, ∑P_k = 1, где суммирование распространяется на все возможные значения к.

Перечень всех возможных значений ДСВ и соответствующих этим значениям вероятностей называется законом распределения дискретной случайной величины.

Зная закон распределения ДСВ, можно вычислить функцию распределения, представляющую собой, в силу определения (1.1), функцию накопленных вероятностей:

где суммирование распространяется на все значения индекса i, для которых x_i < х. Из этой формулы, в частности, следует, что

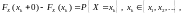
т.е. функция распределения ДСВ испытывает скачки в точках х, для которых существует положительная вероятность события {X = х}.

Случайная величина X называется непрерывной случайной величиной (НСВ), если существует такая неотрицательная, интегрируемая по Риману в бесконечных пределах функция 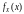, называемая плотностью распределения вероятностей, что при всех

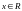
Плотность распределения вероятностей обладает следующими свойствами:

1. 

2. 

3. 

Функция распределения непрерывной случайной величины 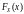является непрерывной монотонно возрастающей функцией на всей оси, причем 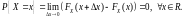Это значит, что вероятность того, что НСВ 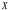примет конкретное значение равна нулю.

Вероятность попадания НСВ на интервал может быть вычислена как через функцию распределения по формуле (1.2), так и через плотность распределения вероятностей:

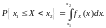(1.3)

Случайные величины, помимо законов распределения, могут также описываться числовыми характеристиками, среди которых различают характеристики положения (математическое ожидание, мода, медиана и др.) и характеристики рассеивания (дисперсия, среднеквадратичное отклонение, различные моменты распределения порядка выше первого и др.).

Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа случайной величины X формулой

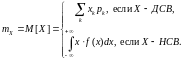(1.4)

Математическое ожидание существует, в частности, если ряд (соответственно интеграл) в правой части формулы (4) сходится абсолютно.

Модой непрерывной случайной величины X называется действительное число d_x, определяемое как точка максимума плотности распределения вероятностей f_x(x).

Мода дискретной случайной величины определяется как такое возможное значение х_т, для которого

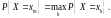
Таким образом, мода ДСВ есть ее наиболее вероятное значение в случае, если такое значение единственно.

Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь множество значении (мультимодальное распределение).

Медианой непрерывной случайной величины X называется действительное число h_x, удовлетворяющее условию

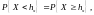
т.е. корень уравнения

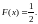
Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.

Дисперсией случайной величины X называется неотрицательное число , определяемое формулой

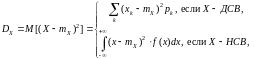(1.5)

Дисперсия существует, если ряд (соответственно интеграл) в правой части равенства сходится. Неотрицательное число называется среднеквадратичным отклонением случайной величины X. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. (Величину иногда называют стандартным отклонением.) Если величина X = const (т.е. X не случайна), то .

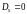Случайная величина X называется центрированной (обозначается 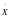), если т_х = 0. Случайная величина называется стандартизованной, если .

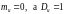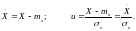
Начальным моментом т-го порядка (т = 0, 1, 2, . ..) распределения случайной величины X (если он существует) называется действительное число , определяемое по формуле

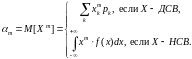(1.6)

Центральным моментом т~го порядка распределения случайной величины X (если он существует) называется число , определяемое по формуле

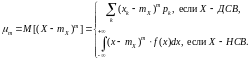(1.7)

Из определений моментов, в частности, следует, что

С моментами высшего порядка связаны ещё две числовые характеристики:

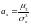-коэффициент асимметрии или «скошенности» распределения,

- коэффициент эксцесса или «островершинности» распределения.

Квантилью уровня 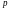функции распределения 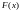СВ называется минимальное значение 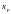, при котором функция распределения не меньше значения , где 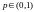, т. е.

(1.8)

На рис. 1 показаны квантили уровней некоторой функции распределения , а на рис. 2 – квантили уровней 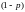и для симметричной относительно нуля плотности распределения .

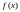Рис. 1

Рис. 2.

Критической точкой порядка р распределения непрерывной случайной величины X называется действительное число , удовлетворяющее уравнению

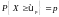
Квантиль и критическая точка одного и того же распределения связаны простым соотношением:

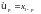
Лекция 2. Основные распределения случайных величин. Основные дискретные распределения Биномиальное распределение

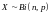Дискретная СВ X с реализациями , имеет биномиальное распределение с параметрами и , что символически записывается как , если вероятность события 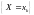определяется формулой Бернулли:

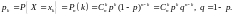(2.1)

Числовые характеристики биномиального распределения:

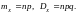(2.2)

Правая часть формулы Бернулли совпадает с выражением для (к + 1) -го слагаемого в разложении бинома Ньютона , поэтому такое распределение называется биноминальным .

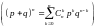Наиболее вероятное значение биномиально распределённой случайной величины 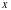удовлетворяет неравенству

.

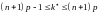Ряд распределения биномиальной величины приведён в таблице

X	0	1	…	k	…	n-1	n
P			…		…

Условия возникновения. Проводится n одинаковых независимых опытов, в каждом из которых событие А появляется с вероятностью р. Случайная величина X - число опытов, в которых произошло событие А (см. теорему о повторении опытов) имеет биномиальное распределение.

Геометрическое распределение

Дискретная СВ X с реализациями 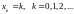, имеет геометрическое распределение с параметром , что символически записывается как , если вероятность события определяется формулой:

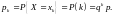(2.3)

Числовые характеристики геометрического распределения:

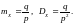(2.4)

Вероятности 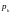образуют геометрическую прогрессию с первым членом 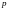и знаменателем 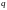, поэтому это распределение называется геометрическим.

Ряд распределения величины, распределённой по геометрическому закону приведён в таблице

X	0	1	…	k	…
P			…		…

Условия возникновения. Проводится ряд одинаковых независимых опытов до первого появления некоторого события А. Случайная величина X - число проведенных безуспешных опытов до первого появления события А.

Распределение Пуассона

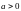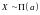Дискретная СВ X с реализациями , имеет распределение Пуассона с параметром , что символически записывается как , если вероятность события определяется формулой:

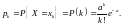(2.5)

Числовые характеристики распределения Пуассона:

(2.6)

Наиболее вероятное значение пуассоновской случайной величины удовлетворяет неравенству

.

На практике СВ имеет, как правило, физическую размерность. В этом случае физические размерност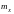и и не совпадают, хотя их числовые значения для распределения Пуассона равны.

Распределение Пуассона является предельным случаем биномиального, когда число опытов п неограниченно увеличивается 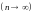, а вероятность р события A в одном опыте стремится к 0 , так что существует предел

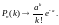
Поэтому при больших и малых двухпараметрическое биномиальное распределение можно приближенно заменить однопараметрическим распределением Пуассона 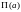, где 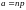. Ошибка от такой замены не превышает :

Ряд распределения величины, распределённой по закону Пуассона приведён в таблице

X	0	1	…	k	…
P			…		…

Условия возникновения. Распределение Пуассона широко используется в теории массового обслуживания при описании потоков случайных событий.

Рассмотрим временную ось, на которой будем отмечать моменты возникновения случайных событий (например, отказы компонентов в сложном техническом устройстве, заявки на обслуживание и т.п.). Последовательность таких моментов называется потоком случайных событий.

Поток случайных событий называется стационарным, если число событий, приходящихся на интервал , в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени X (интенсивность потока - 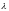) постоянно.

Поток случайных событий называется ординарным, если вероятность попадания в некоторый малый участок двух и более случайных событий значительно меньше, чем вероятность попадания одного события.

В потоке отсутствует последействие, если вероятность попадания событий на участок не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.

Поток случайных событий называется пуассоновским, если он является ординарным и без последействия. Пуассоновский поток случайных событий называется простейшим, если он стационарный.

Распределение событий простейшего потока с интенсивностью на временном интервале длиной является пуассоновским:

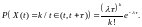(2.7)