
- •2) Для любого положительного числа в множестве m можно найти число , такое что
- •Доказательство.
- •Арифметика бесконечно малых последовательностей.
- •Доказательства:
- •Доказательство:
- •Доказательство:
- •Примеры:
- •Следствие (т. О промежуточном значении непрерывной функции):
- •Доказательство:
- •Доказательство:
- •Производная сложной функции.
- •2)Доказательство аналогично.
- •Доказательство.
Доказательство:
Докажем,
что
![]()
![]() .
.
Предположим
противное, то есть
![]()
![]()
 .
Возьмем
.
Возьмем
![]() =1,2,3…
=1,2,3…
Получим
![]() :
:
1)
![]()
![]()
![]()
2)
![]()
Из
этих определений получаем
![]()
![]() .
.
![]()
![]() =>
=>
![]() -подпоследовательность
последовательности
-подпоследовательность
последовательности
![]() :
:
![]() .
.
![]() -непрерывна
в точке
-непрерывна
в точке
![]() =>
=>
![]() .
.
![]() -подпоследовательность
последовательности
-подпоследовательность
последовательности
![]() :
:
![]() =>
=>
![]() .
Противоречие.
.
Противоречие.
Замечание:
Замкнутость
![]() по
существу.
по
существу.
![]() ,
,
![]() ,
но
,
но
![]()
Не
является ограниченной на
![]() .
.
БИЛЕТ 24. Вторая теорема Вейерштрасса.
Пусть
![]() .
Тогда
.
Тогда
![]()
Замечание:
Непрерывная на отрезке
![]() функция на этом отрезке достигает
своего наибольшего и наименьшего
значения, причем в условиях теоремы
отрезок по существу.
функция на этом отрезке достигает
своего наибольшего и наименьшего
значения, причем в условиях теоремы
отрезок по существу.
Доказательство:
По
условию теоремы
![]() =>
=>
![]() ограничена
на
ограничена
на
![]() =>
=>
![]() Докажем, что
Докажем, что
![]() .
Предположим противное, то есть
.
Предположим противное, то есть
![]()
![]()
![]() .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
![]() на
на
![]() .
По 1 теореме Вейерштрасса
.
По 1 теореме Вейерштрасса
![]() ограничена
на
ограничена
на
![]() ,
то есть
,
то есть
![]()
![]()
![]() .
.
![]()
![]()
![]() (<
(<![]() )-
верхняя граница.
)-
верхняя граница.
![]() ,
то есть
,
то есть
![]()
![]() .
.
Противоречие.
Следствие:
если
![]() ,
то
,
то
![]() .
.
БИЛЕТ 25. Равномерная непрерывность и непрерывность в точке. Теорема Кантора (без доказательства).
Определение
1:
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если
,
если
![]() .
.
Определение
2:
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если
,
если
![]()
![]() ,
,
![]() .
.
Определение
3:
Функция
![]() непрерывна
в точке
непрерывна
в точке
![]() ,
если
,
если
![]()
![]()
![]()
![]()
![]() .
.
Функция, непрерывная на отрезке.
Определение:
Функция
![]() называется
непрерывной на отрезке
называется
непрерывной на отрезке
![]() ,
если она непрерывна в каждой внутренней
точке этого отрезка, непрерывна справа
в точке
,
если она непрерывна в каждой внутренней
точке этого отрезка, непрерывна справа
в точке
![]() и
непрерывна слева в точке
и
непрерывна слева в точке
![]() .
.
Теорема
Кантора:
Если функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() ,
то для любого
,
то для любого
![]() можно указать такое
можно указать такое
![]() ,
что
,
что
![]() для любых
для любых
![]() и
и
![]() из
из
![]() таких, что
таких, что
![]() .
.
+ БОНУС
Доказательство:
Возьмем
число
![]() .
Построим на отрезке
.
Построим на отрезке
![]() точки
точки
![]() следующим образом: если точка
следующим образом: если точка
![]() уже построена, то рассмотрим множество
уже построена, то рассмотрим множество
![]() ,
состоящее из всех точек
,
состоящее из всех точек
![]() ,
удовлетворяющих неравенствам:
,
удовлетворяющих неравенствам:
![]() ,
,
![]() .
.
Положим (см. рисунок), что:
![]()
если
![]() пусто (и на этом построение заканчивается).
пусто (и на этом построение заканчивается).
если
![]() не пусто.
не пусто.

Заметим,
что
![]() в силу непрерывности
в силу непрерывности
![]() и
и
![]() для любого
для любого
![]() из отрезка
из отрезка
![]() .
Последовательность
.
Последовательность
![]() может быть конечной или бесконечной.
Предположим, что она бесконечна, тогда
может быть конечной или бесконечной.
Предположим, что она бесконечна, тогда
![]() для
всех
для
всех
![]() .
Пусть
.
Пусть
![]() .
Так как
.
Так как
![]() ,
то функция
,
то функция
![]() непрерывна в точке
непрерывна в точке
![]() слева,
и потому можно указать такое число
слева,
и потому можно указать такое число
![]() ,
что
,
что
![]() и
и
![]() для любого
для любого
![]() из интервала
из интервала
![]() .
По определению числа
.
По определению числа
![]() можно
найти
можно
найти
![]() в
интервале
в
интервале
![]() .
Тогда любое число
.
Тогда любое число
![]() из интервала
из интервала
![]() принадлежит
интервалу
принадлежит
интервалу
![]() ,
и потому
,
и потому
![]()
![]()
![]() ,
что противоречит тому, что
,
что противоречит тому, что
![]() .
Таким образом, последовательность
.
Таким образом, последовательность
![]() не
может быть бесконечной, и потому
существует такой номер
не
может быть бесконечной, и потому
существует такой номер
![]() ,
что
,
что
![]() .
Положим:
.
Положим:
![]() .
Возьмем два любых числа
.
Возьмем два любых числа
![]() и
и
![]() из отрезка
из отрезка
![]() таких, что
таких, что
![]() .
Тогда возможны два случая: или обе эти
точки попали на некоторый отрезок
.
Тогда возможны два случая: или обе эти
точки попали на некоторый отрезок
![]() и тогда
и тогда
![]() ,
или этого не случилось, и тогда найдется
точка
,
или этого не случилось, и тогда найдется
точка
![]() между
между
![]() и
и
![]() .
Но в этом случае
.
Но в этом случае
![]() ,
так как
,
так как
![]() и (доказывается аналогично)
и (доказывается аналогично)
![]() ,
а потому
,
а потому![]() .
Так как все приведенные рассуждения
справедливы для любого
.
Так как все приведенные рассуждения
справедливы для любого
![]() ,
то теорема доказана.
,
то теорема доказана.
Смысл
этой теоремы
состоит в том, что для всех точек отрезка
можно по заданному числу
![]() подобрать общее для всех точек
подобрать общее для всех точек
![]() число
число
![]() (фигурирующее в определении). Для
функций, непрерывных на интервале это
можно сделать уже не всегда.
(фигурирующее в определении). Для
функций, непрерывных на интервале это
можно сделать уже не всегда.
БИЛЕТ 26. Дифференцируемость функции. Дифференциал. Понятие производной функции.
Определение:
Пусть функция f(x)
определена в окрестности точки
![]() .Если
ее приращение
.Если
ее приращение
![]() можно представить в виде
можно представить в виде
![]() ,то
говорят ,что f(x)
дифференцируема в точке
,то
говорят ,что f(x)
дифференцируема в точке
![]() (иногда
пишут
(иногда
пишут
![]() -величина
более высокого порядка, чем
-величина
более высокого порядка, чем
![]() а это означает, что
а это означает, что
![]() )
)
![]()
![]() -линейная
функция от
-линейная
функция от
![]() .Она
называется дифференциалом функции
f(x)
и обозначается
.Она
называется дифференциалом функции
f(x)
и обозначается
![]()
Пример:

Критерий дифференцируемости:
Для
того, чтобы функция y=f(x)
была дифференцируема в точке
![]() необходимо и достаточно, чтобы
существовала производная в этой точке.
необходимо и достаточно, чтобы
существовала производная в этой точке.
Доказательство:
1.Необходимость.
f(x)
дифференцируема в точке
![]() это означает
это означает
![]() .
Разделим это равенство на
.
Разделим это равенство на
![]() и перейдем к пределу
и перейдем к пределу
![]()
![]() ,т.е. существует
,т.е. существует
![]() ,
т.е. производная существует.
,
т.е. производная существует.
2.Достаточность.
Пусть существует
![]() или
или
![]() ,
т.е. f(x)
дифференцируема в точке
,
т.е. f(x)
дифференцируема в точке
![]() .
.
Итак,
![]() ,
т.е.
,
т.е.
![]() .Отсюда
следует новое обозначение производной
.Отсюда
следует новое обозначение производной
![]() и эту величину можно рассматривать как
один символ, так и как частное
дифференциалов.
и эту величину можно рассматривать как
один символ, так и как частное
дифференциалов.
Понятие производной функции.
Определение:
Производной функции
![]() в
точке
в
точке
![]() называется предел
называется предел
![]() Очень удобна более короткая запись для
этого предела и более короткое обозначение
для производной
Очень удобна более короткая запись для
этого предела и более короткое обозначение
для производной
![]() .
.
БИЛЕТ 27. Алгебраические свойства дифференцируемых функций.
Теорема:
Если
функции
![]() и
и
![]() имеют
производные, то
имеют
производные, то
1)
![]() .
.
2)
![]() .
.
3)
![]() (
(![]() постоянная).
постоянная).
4)
![]() .
.
Доказательство:
По теореме об арифметике пределов
функций, по определению производной и
формулам:
![]() ,
,
![]() и
и
![]() имеем:
имеем:
1).![]()
![]()
![]() .
.
2).
![]()
=![]() =
= =
=![]()
![]() +
+![]()
![]() +
+
+
![]() =
=![]() =
=![]() ,
так как множители
,
так как множители
![]() и
и
![]() не зависят от
не зависят от
![]() и
при
и
при
![]()
![]() являются постоянными, а
являются постоянными, а
![]() ,
поскольку
,
поскольку
![]() имеет производную и потому непрерывна.
имеет производную и потому непрерывна.
3).
![]() (так как
(так как
![]() ).
).
4).
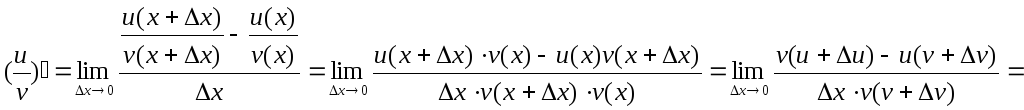 =
=![]()
![]()
![]()
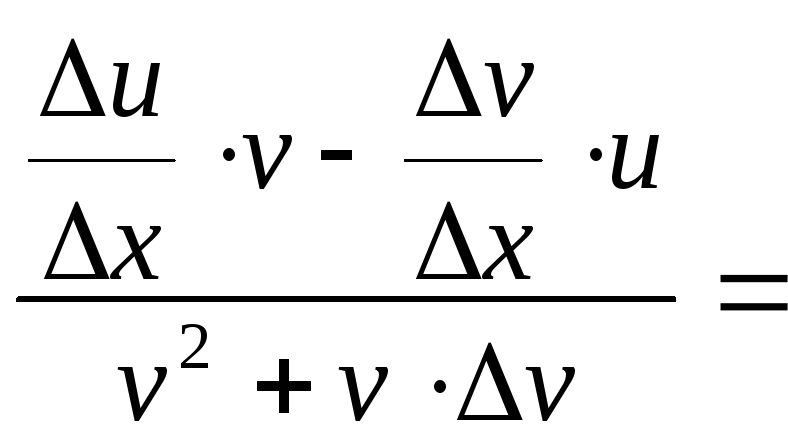
![]() .
.
БИЛЕТ 28. Дифференцирование сложной функции. Инвариантность формы первого дифференциала.
