БИЛЕТ 1. Точные грани числовых множеств. Теоремы существования и единственности.

Точной верхней гранью числового множества () называется число, такое что:

1) S- верхняя граница ( ).

2) Для любого положительного числа в множестве M можно найти число , такое что

>-. ( >-)

Точной нижней гранью числового множества () называется число, такое что:

1) S- нижняя граница ( ).

2) Для любого положительного числа в множестве m можно найти число , такое что

+. ( +)

Теорема существования: Пусть , , ограниченное сверху (снизу), тогда существует точная верхняя (нижняя) грань.

Замечание: (аксиома непрерывности множества действительных чисел).

Пусть , , и , , причем и : . Тогда

: и .

, , ограничено сверху.

, .

, и ,.

и

1)

2) >-

Предположим противное:

:.

- ,

. Получили противоречие.

Аналогично для =.

Теорема единственности: Если числовое множество не пусто и ограничено сверху (снизу), то у него есть единственная ().

Введем следующие условия:

1) числовое множество ограничено сверху, если можно указать такое число , что для всех чисел из множества .

2) числовое множество ограничено снизу, если можно указать такое число , что для всех чисел из множества .

Доказательство:

Рассмотрим множество , состоящее из всех чисел , таких что для любого числа из множества будет . Такие числа существуют, так как множество ограничено сверху. В силу непрерывности множества действительных чисел существует такое число , что для любых чисел (из) и (из).

Покажем, что =. По определению , для всех чисел из множества будет , так что первое условие выполнено. Проверим, что выполнено и второе условие. Предположим, что оно не выполнено, т.е. есть такое положительное число (>0), что для всех чисел из множества будет . Так как , то число не принадлежит множеству . Но это противоречит определению множества , которое было множеством всех чисел , таких что для любого числа из множества будет , а мы нашли число , тоже обладающее таким же свойством и не принадлежащее множеству . Полученное противоречие показывает, что для числа выполнено и второе условие из определения верхней грани.

БИЛЕТ 2. Лемма о вложенных отрезках.

Пусть =, =1,2,…, причем …, то есть ,

. Тогда , то есть .

Доказательство.

Рассмотрим , , ограничено сверху, так как любое является верхней границей множества в силу вложенности отрезков. . Тогда:

а) - верхняя граница , то есть .

б) - наименьшая из всех границ, то есть.

.

Замечание: Если в условиях леммы хотя бы один из концов исключить, то аналогичная лемма будет не верна.

.

( ] ] ] ]

0 1/3 1/2 1

БИЛЕТ 3. Предел числовой последовательности. Единственность предела. Ограни­ченность сходящейся последовательности.

Определение: функцию называют числовой последовательностью.

- члены числовой последовательности.

- номер члена числовой последовательности.

или ,

=, -общий член.

Определение: Число называется пределом последовательности (пишут ), если для любого положительного числа (>0) можно указать такое число , зависящее от , что для всех .

Теорема: (о единственности предела): Если -сходящаяся, то предел единственный.

Доказательство:

Пусть , , .

Для определенности имеем:

.

< <

<. <.

Противоречие.

Теорема: (об ограниченности сходящейся последовательности): Если -сходится, то она ограничена.

- сходящаяся : .

Возьмем =1 .

Обозначим , тогда

, тогда

Отсюда для обоих случаев

Замечание: обратное не верно.

БИЛЕТ 4. Свойства сходящихся последовательностей, связанные с неравенствами.

Теорема: (о предельном переходе в неравенство):

Пусть , . . Тогда .

Замечание:

.

Доказательство (от противного):

Пусть .

Возьмем .

Обозначим

.

- противоречие.

Замечание: Если для элементов последовательности выполняется , то отсюда не следует, что . .

=, =, .

Теорема (о промежуточной последовательности).

Пусть , и . Тогда существует .

Замечание:

().

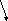
Доказательство:

Возьмем произвольный .

. Тогда . . ().

.

Теорема: (об отделимости от нуля).

Пусть и . Тогда .

Замечание: - ограниченная.

().

.

.

БИЛЕТ 5. Бесконечно малые и ограниченные последовательности. Арифметика бес­конечно малых последовательностей.

Определение: Последовательность будем называть бесконечно малой последовательностью, если , то есть .

Теорема: бесконечно малая последовательность.

(I)-

(II)-

(I) (II) =

(II)(I) =

Замечание: Фактически мы дали эквивалентность определений сходящейся последовательности.

Определение: Последовательность будем называть ограниченной последовательностью, если .

Замечание: Ранее мы доказали, что всякая сходящаяся, в том числе и бесконечно малая последовательность ограничена.