1. Необходимые условия.

1. Уравнение Эйлера – это необходимое условие первого порядка.

2. Необходимые условия второго порядка:

• необходимое условие второго порядка – условие Лежандра. Оно заключается в том, что:

Этот вывод следует из необходимости условия второго порядка

для существования максимума функции

при

• условие Вейерштрасса.

Если траектория решения и- любая другая допустимая траектория, то функция

Функция называется функцией Вейерштрасса.

Условие Вейерштрасса аналогично условию вогнутости целевой функции в статическом случае.

Если функция является вогнутой относительно управляющего параметра, то условие Вейерштрасса выполнено.

• условия Вейерштрасса – Эрдмана для точки излома допустимой траектории

Эти условия не имеют прямой аналогии в статических задачах, поскольку они существенным образом зависят от времени.

Хотя фазовая траектория является непрерывной, управлениедолжно быть только кусочно - непрерывной функцией.

может состоять из кусков непрерывных кривых, соединенных точками излома, в которых разрывна.

Рисунок 12.2.3

Условия Вейерштрасса – Эрдмана требуют, чтобы

и были непрерывны в точках излома.

где - означают пределы в точкеслева и справа.

Задача классического вариационного исчисления с - фазовыми координатами имеет вид:

где

, .

Необходимые условия:

1. Уравнение Эйлера:

Граничные условия:

.

2. Условие Лежандра:

Матрица отрицательно определена или отрицательно полуопределена.

3. Условие Вейерштрасса:

4. Условие Вейерштрасса - Эрдмана

и являются непрерывными в точке излома.

Здесь:

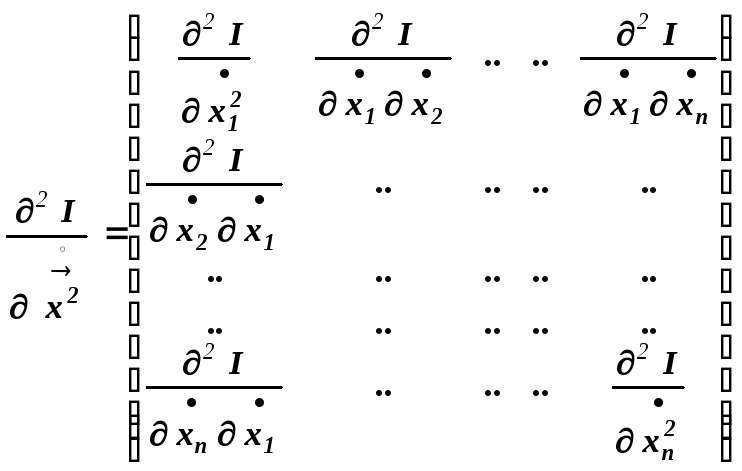
Таким образом уравнение Эйлера распадается на :

.

Ограничения.

1. Изопериметрическая задача

,

где

-заданная непрерывно дифференцируемая функция,

- заданная константа.

Вводится множитель Лагранжа и определяется функционал:

Уравнение Эйлера

Это уравнение вместе с граничными условиями определяет решение.

Для изопараметрических задач выполняется важный принцип взаимности, согласно которому, если максимизирует при условии, чторавно постоянной величине, томинимизирует при условии, чторавно постоянной величине.

Например,

кривая постоянной длины, ограниченная площадь которой максимальна, является также кривой с минимальной длиной, ограничивающей заданную площадь. Такой кривой является окружность.

2. Другой вид ограничений - в форме равенства.

где

- заданный вектор - столбец, составленный из функций.

- заданный вектор - столбец.

- число степеней свободы задачи.

Предполагается, что ранг матрицы Якоби равен :

Вводятся множителей Лагранжа(вектор):

составляется функция Лагранжа:

и тогда нужно выбрать функцию , минимизирующую функционал:

и вектор, минимизирующий.

Уравнение Эйлера

совместно с граничными условиями и ограничениями типа равенства, определяют решение задачи.

3. Ограничения в форме неравенства.

где

- заданный вектор - функция размерности .

Строится функция Лагранжа, так же как в предыдущем случае.

Тогда решение ищется из

- уравнение Эйлера.

- условия Куна - Таккера.

Из условий Куна – Таккера вытекают условия дополняющей нежесткости, состоящие в том, что любой множитель Лагранжа равен нулю, если соответствующее ограничение выполняется как строгое неравенство и что любое ограничение выполняется как равенство, если соответствующий множитель Лагранжа положителен.

Замечание.

С помощью задач вариационного исчисления можно решать ряд задач управления с определенными типами ограничений.

Однако принципиальный недостаток классического вариационного исчисления состоит в том, что оно неприемлемо для непосредственного решения задач, в которых значения управляющих параметров принадлежат фиксированной области. Этот недостаток преодолен в новых подходах в динамическом программировании и в принципе максимума.