5.1.3. Многокритериальное оптимальное планирование

Большинство задач планирования в реальных организационных системах носит многокритериальный характер и может быть представлено задачей многокритериального линейного программирования в виде:

, ; (5.20)

(5.21)

(5.22)

, ; (5.23)

, ,; (5.24)

, , (5.25)

где f_l– частный критерий оптимальности;

L – количество частных критериев оптимальности;

–коэффициенты частного критерия оптимальности ,;

b_j– запасы j-го вида ресурса, предназначенного для выполнения оптимального плана, ;

a_ij- расход j-ого ресурса на выпуск единицы i-го вида продукта.

С методами решения детерминированных задач многокритериальной оптимизации, определяемых условиями (5.20) – (5.22), можно ознакомиться в [14].

Графическое представление задачи многокритериального линейного программирования показано на рис. 5.8.

Рис. 5.8

Методика определения решений многокритериальной задачи оптимизации в условиях неопределенности (5.20) – (5.25) представлена в [14].

Для иллюстрации определения области решений напомним о некоторых определениях, данных в [14], и рассмотрим практический пример.

Определение 1.

Из двух точек точканазываетсядоминирующей по отношению к (), если для всех выполняется и, кроме того, по крайней мере, для одного j .

Определение 2.

Точка называетсяулучшаемой, если существует хотя бы одна точка , такая, что,и хотя бы для одногоj: , в противном случае точкане улучшаемая или эффективная.

Определение 3.

Множество S₁, состоящее из эффективных точек, называется множеством решений, оптимальных по Парето.

Для определения области Парето необходимо использовать следующее правило [14]:

если все вектора, указывающие направления улучшения критериев (направление улучшения критерия совпадает с направлением градиента функции , если, и с направлением антиградиента функции, если) принадлежат открытой полуплоскости, проведенной через начало координат в системе координат (с₁, с₂), то решением многокритериальной задачи оптимизации (5.20) – (5.22) является область Парето, представляющая часть границы допустимой области решений, в противном случае областью решений многокритериальной задачи будет вся допустимая область.

Пример 3.

Банк имеет возможность инвестировать финансовые ресурсы в размере 10 млн долларов в два проекта. При инвестировании в первый проект прибыль составляет 30% годовых, при инвестировании во второй проект - 35% годовых. Потери от риска при вложении в первый проект составляют 6% годовых, во второй проект – 6,5% годовых. Какое количество финансовых средств банк должен вложить в первый и во второй проекты, чтобы получить максимальную прибыль и обеспечить минимальные потери от риска?

f₁ = 0,3x₁ + 0,35x₂  max;

f₂ = 0,06x₁ + 0,065 x₂  min;

x₁ + x₂  10;

x₁ > 0; х₂ > 0.

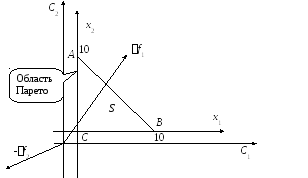
Рис. 5.9

Решением задачи по критерию f₁ max является точка А, решением задачи по критерию f₂ min является точка С. Решением двукритериальной задачи будет отрезок прямой АС, представляющий собой множество Парето.

Определение устойчивости оптимальных плановых решений при использовании детерминированной модели многокритериального линейного программирования вида (5.20) – (5.22) при интервальной неопределенности параметров может быть проведено с использованием методов, указанных в [14].