III. Запись результата косвенного измерения.

При записи результата косвенного измерения необходимо соблюдать следующие правила:

1. Величину абсолютной погрешности необходимо округлить до двух зна­чащих цифр, если первая из них единица, и до одной во всех остальных случаях (значащими цифрами называются все цифры, кроме нулей, стоящие впереди числа слева). Нули в середине числа и в конце являются значащими. Например, в числе 0.0305 три значащие цифры, в числе 5100  четыре значащие цифры.

Пример. Если при определении объема цилиндра V абсолютная ошибка оказалась рав­ной 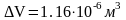, ее следует округлить до двух значащих цифр: 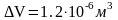. Если 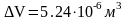, ее следует округлить до одной значащей цифры .

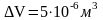2. Среднее значение измеряемой величины следует записать таким образом, чтобы результат заканчивался в том же разряде, что и абсолютная погрешность.

Пример. Если объем цилиндра при расчете по формуле 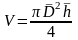получается равным 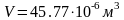, а абсолютная ошибка после округления равна , то объем следует записать также только до десятых

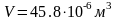
Окончательный результат записывается в виде: .

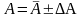Такая запись показывает, в каких пределах содержится истинное значение измеряемой величины.

В случае нашего примера для объема цилиндра окончательный результат записывается следующим образом: .

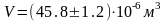Такая запись указывает, что истинный результат лежит в пределах:

.

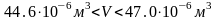ПРИМЕР ОБРАБОТКИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ.

При определении ускорения свободного падения g с помощью математи­ческого маятника используется расчетная формула:

,

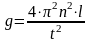где l  длина математического маятника, измеряемая миллиметровой линейкой, n - число колебаний маятника, t - время десяти колебаний маятника, определяемое секундомером. После прямых измерений времени и длины получаем следующие данные:

t = 14.72с, 14.74с, 14.75с, 14.73с, 14.76; n = 10;

l= 54.2 см ±0.05 см = (54.2 ±0.05)10^-2 м

1. Результаты измерений заносим в таблицу

2) Определяем погрешности при прямых измерениях:

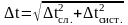
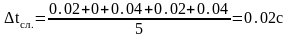
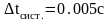
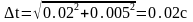
t = (14.74±0.02) c.

б) Так как измерения длины производились один раз, в качестве абсолютной погрешности берем погрешность инструмента (линейки), т.е. половину деления ее шкалы

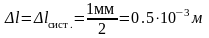
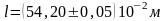
3) Определяем относительную погрешность при косвенном измерении g:

а) берем натуральный логарифм от выражения:

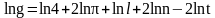
б) выполняем дифференцирование

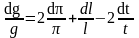
в) знак d заменяем на знак

,

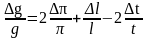г) знак минус перед знаком заменяем на знак плюс

.

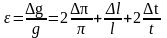Число 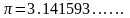Если ограничиться значением 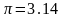, то

относительная погрешность 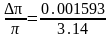и

.

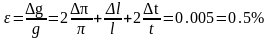5. Запись окончательного результата. Находим среднее значение ускорения свободного падения

.

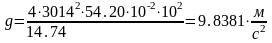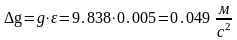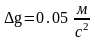Найдем абсолютную погрешность: . Округляем полученный результат до одной значащей цифры . Записываем окончательный результат:

.
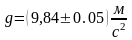