Лабораторная работа № 000 обработка результатов измерений на примере задач определения обьема цилиндра и измерения силы тока в цепи

Цель работы: ознакомиться с методом обработки результатов измерений.

Приборы и принадлежности: цилиндр, штангенциркуль, микрометр.

Теория погрешностей

I. Погрешности при прямых измерениях

Прямыми измерениями называются такие, при которых измерение величины производится непосредственно по шкале прибора. Например,

измерение длины штангенциркулем, измерение веса тела на весах, определение промежут­ков времени с помощью секундомера. Если отклонение результатов измерений от истинного значения измеряемой величины происходит как в сторону увеличения, так и в сторону уменьшения результатов из­мерений, то наиболее вероятным значением измеряемой величины будет среднее арифметическое всех сделанных измерений:

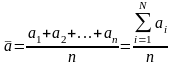, (1)

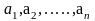
где  результаты отдельных измерений, n  число измерений.

Для характеристики степени приближения к истинному значению измеря­емой величины вводится понятие абсолютной погрешности  величины, показы­вающей насколько найденное (среднее арифметическое) значение может отли­чаться от истинного значения измеряемой величины.

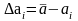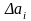
Для определения абсолютной погрешности сначала нужно найти отклонения каж­дого отдельного измерения от среднего арифметического: , где  отклонение данного измерения, равное разности между сред­ним значением измеряемой величины 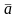и результатом этого измерения .

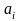Случайная погрешность вычисляется по формуле:

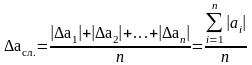, (2)

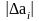
где  модули отклонений каж­дого отдельного измерения от среднего арифметического значения.

Из формулы (2) и теории вероятностей следует, что с увеличением числа измерений n случайная погрешность будет уменьшаться.

В качестве систематической погрешности берется приборная погрешность, равная половине цены деления шкалы прибора. Ценой деления прибора называется минимальная величина, измеряемая прибором.

В общем случае необходимо принимать во внимание как случайные, так и систематические погрешности прямых измерений. Поэтому абсолютная пог­решность 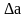при прямых измерениях рассчитывается по формуле:

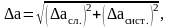(3)

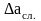
где  случайная погрешностей, определяемых по формуле (2),

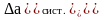систематическая погрешность прибора, инструмента.

Примечание: Если случайная погрешность много меньше систематической, то для повышения точности результата измерений нет смысла увеличивать число измерений, а нужно принять меры к уменьшению систематической погрешности (например, использовать более точные приборы).

Пример. Пусть измеряется диаметр цилиндрического стержня с помощью штанген­циркуля и делается 5 измерений: 34.50 мм, 34.65 мм, 34.30 мм,

34.70 мм, 34.55 мм.

Среднее арифметическое всех сделанных измерений:

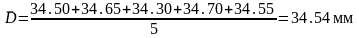
Полученное значение 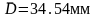даёт наиболее вероятное значение измеряемой величины D.

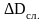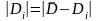Для нахождения случайной погрешности нужно найти абсолютное значение отклонения каждого из 5-ти измерений от среднего арифметического и затем определить среднее значение этих отклонений:

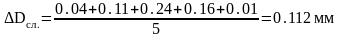
Цена деления штангенциркуля равна 0.05 мм, следовательно, систематическая погрешность равна .

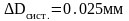Абсолютная погрешность при измерении диаметра стержня:

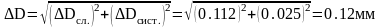
Результат измерений принято записывать следующим образом:

.

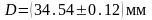(Результат измерений 34,54 мм и абсолютная погрешность 0,12 мм должны заканчиваться в одинаковом разряде)

Для характеристики точности измерения вводится понятие относительной погрешности:

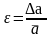
Относительная погрешность ε представляет собой отношение абсолютной погрешности к среднему значению измеряемой величины. В нашем примере относительная погрешность при измерении диаметра:

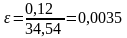
Относительная погрешность является безразмерной величиной. Она показывает, какую часть измеряемой величины составляет абсолютная погрешность.