4.2. Дельта метод
Некоторые работы были выполнены для решения проблем мнимых решений. Были использованы различные алгоритмы, основанные на усечении функции рассеивания фаз. Дельта метод наиболее эффективный среди них; он может быть обобщен и в векторном случае [9]. Как и в скалярном случае, функция рассеивания представляется в виде суммы дельта-функций и гладкой части.
(31)
Здесь
f
является мнимой частью рассеивания;
– единичная матрица.
Уравнение (31) для греческой матрицы (11) можно записать как
(32)
Этот этап матричных преобразований приводит к масштабным преобразованиям оптической глубины и коэффициента альбедо рассеивания.
. (33)
Таким образом, дельта метод может значительно уменьшить K. Однако такой подход искажает первоначальную краевую задачу и приводит к ошибке в малом значащем угле (мы не полагаем, что фракция аэрозолей крупная) или колебания в угловом распределении излучений.
4.3. Tms и ims-методы
Для устранения упомянутых выше проблем в решении ВУПИ Накаджима и Тенака [10] обратились к идее определения мнимой части в решении, основываясь на аппроксимации аналитического представления углового распределения параметров Стокса первого и второго порядков рассеивания:
(34)
Здесь первые два порядка удовлетворяют уравнениям:
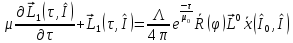(35)
(36)
Уравнения
(35) и (36) решаются аналитически. Однако
решение уравнение (36) вычисляется с
помощью тройного интеграла, и время
выполнения его расчета может превысить
время решения исходной задачи (26). По
этой причине, как правило, используется
приближение, описанное разбиением
параметров Стокса в окрестности
инцидентного направления. Наиболее
эффективным способом решения является
приближение малыми углами, где дисперсия
рассеиваемых и не рассеиваемых лучей
не принимается во внимание. Это приближение
эквивалентно изменению параметра
в формулах (35) и (36) на
.
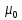Наиболее известные коды, использующие
как дельта метод, так и TMS
метод, – DISORT
[11] в скалярном случае и Pstar
[12] – в векторном.
4.4. Метод малых угловых изменений сферических гармоник
Может
быть показано, что естественной эволюцией
TMS-метода
является включение в
всех порядков рассеивания в малом
угловом приближении [6]. Этот подход
описан в [6] на основе метода малых угловых
модификаций сферических гармоник.
В
этом случае мнимая часть углового
распределения параметров Стокса в
CP-представлении
расширен сферическими функциями с
инцидентным направлением
:
(37)
здесь
,
𝛙
– азимут
в системе относительно
.
Спектр сильного мнимого углового распределения – гладкая функция гармонических индексов k. По этой причине можем получить дифференциальное уравнение [6] для коэффициентов разложения
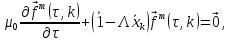(38)
решением которого является
(39)
После преобразования SP-представления МСГ [6] решение может быть представлено в системе координат вокруг нормали к границе слоя:
(40)
где
.
После подстановки выражения (40) в (4) и после некоторых преобразований [6], получаем выражение для функции источника
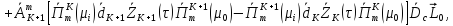(41)
где
,
.
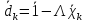Такой подход приводит реальную часть решения почти мнимой функцией. Таким образом, M может быть небольшой, N практически не зависит от K. Этот метод ликвидации мнимой части решения реализован в двух кодах: МДО в скалярном и векторном случаях. Оба кода реализованы на языках Fortran и MATLAB [13].