3. Решение регулярной части

Решение полученное системы уравнений имеет аналитический вид [4, 7] в матричной форме

(22)

Выражение (22) эквивалентно решению, представленному в качестве суммы общего решения однородной системы и частного решения неоднородной системы уравнений [8]. Матричное представление является наиболее удобным для аналитических преобразований и применения к решению вычислительной техники. Решение однородного уравнения

, (23)

соединяет излучения на нижней границе с выражением наверху и называется пропропагатом [7].

Проблема решения (22) связана с отрицательными и положительными показателями в выражении, которое приводит к быстрому ухудшению условий матричной системы. Для того, чтобы устранить этот эффект, мы использовали масштабные преобразования [4]. Матричный показатель представлен в форме [4]

, (24)

где – матрица собственных векторов матрицы и диагональная матрица собственных значений, отсортированных по возрастанию таким образом, что .

Следовательно, уравнение (22) может быть переписано в виде

, (25)

где .

Отметим, что выражение (25) содержит показатель только с положительной силой. Выражая в уравнении (25) исходящее излучение из слоя падающего излучения находим гладкую регулярную часть решения в виде так называемых рассеивателей [7]:

(26)

где

Полученная система (26) является искомым решением, описывающим распределение яркости отраженного и передаваемого излучений. Заметим, что выражение (26) является строгим аналитическим решением краевой задачи для ВУПИ, дискретизированным МДО. Переход от ВУПИ (1) к системе (26) возможно в силу возможности ликвидации (2) и замене интеграла рассеяния (дискретизация) Гауссовой квадратурой (18).

Решение (26), полученное в виде рассеивателей, имеет функциональный тип и позволяет вводить фотометрическую концепцию фактора излучения слоев, используя отражения или передачи. Это сразу дает возможность сформулировать метод матричных операций, чтобы заместить два соседних слоя экливалентным, описанным выражением, идентичным (32), но с эффективными параметрами [3]. Следовательно, решение в виде рассеивателей инвариантно.

Уравнение (26) может быть переписано в форме, похожей на пропагатор (23):

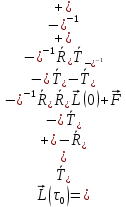. (27)

Такая трансформация была названа «звездным произведением» [7]. Так как дифференциальное уравнение (23) для пропагатора известно, имеем возможность получить одномерную задачу с начальными условиями матричного уравнения Рикатти для матрицы элементов рассеивателей [7] например, отражение:

, (28)

и аналогично для передачи .

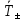Легко видеть, что уравнение (28) эквивалентно уравнению Амбарцумяна-Чандрасекара [8], полученного по принципу инвариантных вложений. Таким образом, после удаления анизотропной части и дискретизации уравнения мы получим единственное аналитическое решение в матричной форме (26). В этом смысле метод последовательных порядков рассеяния является итерационным методом для нахождения обратной матрицы в (26), а метод Монте-Карло – стохастический.

Реализация предложенного решения (26) в качестве алгоритма включает вычисление следующих компонент: нулей и весов квадратурной формулы для дискретизации ВУПИ (18), функций источника (4), собственных векторов и значений матрицы системы (24), произведений матриц (26).

Практическая реализация указанного алгоритма зависит в основном от размеров матриц в (26). Заметим, что (26) получено для реальной части, таким образом, размер зависит в основном не от средних оптических параметров и граничных условий, а от устраненной мнимой части решения. В общем случае, . Однако, в случае правильного устранения мнимой части решения, когда гладкая реальная часть находится в окрестности изотропного углового распределения, вполне возможно, что . Это значительно повышает производительность алгоритма.

4. Ликвидация мнимой части решения

Проанализируем и сравним все основные известные методы ликвидации мнимой части решения с точки зрения уменьшения размеров M и N матрицы и повышения эффективности поиска решения (26).

4.1 Ликвидация прямых излучений без рассеивания

Впервые Эддингтон предложил устранить мнимую часть путем вычислений прямых не рассеивающихся излучений на основе закона Бугера, Милн развил эту теорию, которая подтвердилась в работах Чандрасекара [8]. Таким образом, выражение для прямого не рассеивающегося излучения на плоскости совпала с плоскостью падения, определяющейся по формуле:

(29)

где – вектор параметров Стокса падающего излучения, – нормаль к лучу излучения, p, q – линейная и круговая степени поляризации луча, – азимут поляризации.

В этом случае функция источника в уравнении для реальной части принимает вид:

(30)

В этих условиях излучение рассеивается на малые углы и незначительно отличается от прямого излучения, и этот метод становится неэффективным. Большое рассеяние приводит к значительному увеличению числа членов разложения матрицы рассеяния в ряд по обобщенным сферическим функциям K, что, соответственно, увеличивает размеры матрицы N и M в решении (26).