1.2.3. Методика расчета случайных ошибок прямых измерений

Пусть измеряется n - раз некоторая физическая величина X. Из-за случайных погрешностей, возникающих в процессе измерения, мы получаем набор значений Х₁, Х₂, Х₃, ..., Х_n.

Наиболее близким к истинному значению Х_ист будет среднее арифметическое

.

Чем больше число измерений, тем ближе <Х> к Х_ист, а при .

В реальном эксперименте число измерений всегда ограничено, поэтому истинное значение измеряемой величины остается неизвестным. Результаты отдельных измерений и среднее арифметическое <Х> всегда содержат ошибку. Поэтому вместе с результатом измерений нужно указать возможную величину ошибки, т.е. представить результат в виде:

.

Эта запись равнозначна неравенству:

.

Существует несколько способов оценки случайной ошибки . Мы рассмотрим один из них, наиболее часто используемый при обработке результатов эксперимента.

1.2.4. Порядок расчета случайной ошибки прямых измерений

1. Производят n измерений искомой физической величины и вычисляют её среднее значение:

;

2. Находят абсолютные погрешности отдельных измерений

;

3. Рассчитывают среднюю квадратическую погрешность сред­него арифметического

;

4. По заданной доверительной вероятности и числу из­мерений n находят из таблицы коэффициент Стьюдента .

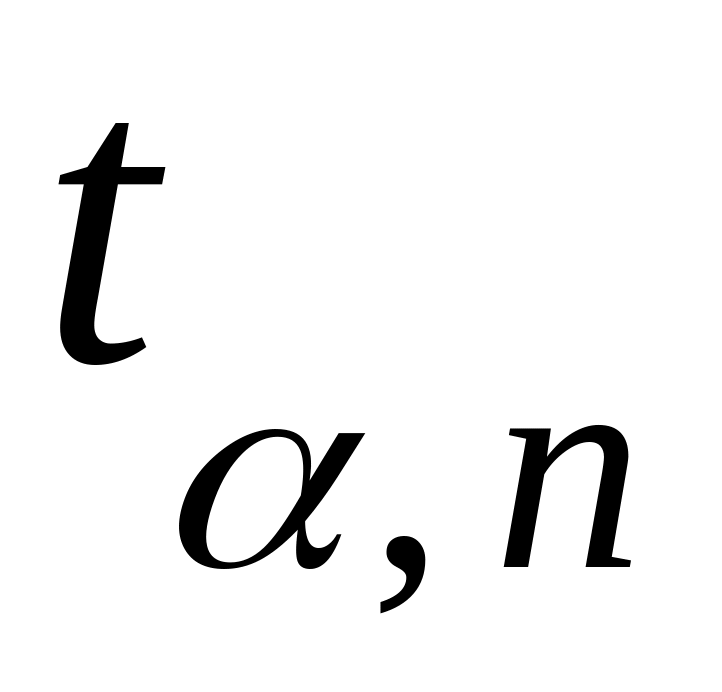5. Рассчитывают абсолютную погрешность:

;

6. Окончательный результат записывают в виде:

, при = 0,95.

Замечания. Так как при малом числе измерений S_<x> является случайной величиной и определяется с большой погрешностью, то при записи числового значения абсолютной погрешности , необходимо учитывать это обстоятельство. В теории ошибок доказано, что при числе измерений в числовом значении достаточно оставить одну значащую цифру, если она больше трех ( =0,528 0,5) и две, если первая из них меньше четырех ( = 0,134 0,13). Затем числовое значение <Х> округляют до разряда ошибки, например:

X= (15,675± 0,525) см (15, 7 ± 0, 5) см.

Точность вычислений при обработке результатов измерений нужно согласовать с точностью самих измерений, ошибка вычислений должна быть на порядок меньше ошибки измерения.

1.3. Рекомендации по выполнению контрольных работ

1.3.1. Общие рекомендации

1. За время изучения кура физики студент-заочник должен выполнить две контрольные работы, в каждой из которых он должен решить 8 задач. В контрольной работе студент должен решить задачи того варианта, номер которого совпадает с последней цифрой его шифра. Номера задач, соответствующих определенному варианту, определяются по таблицам вариантов (см. п. 5).

2. Каждая работа, присланная на рецензию, должна быть выполнена в отдельной ученической тетради, на обложке которой нужно указать фамилию, инициалы, полный шифр, номер контрольной работы, дату её отправки в университет и адрес студента.

3. Условия задач, входящих в контрольную работу, должны быть переписаны полностью, и иметь те номера, под которыми они стоят в методических указаниях. Каждую задачу следует начинать с новой страницы. Для замечаний рецензента следует оставлять поля шириной 4-5 см.

4. Если, несмотря на собственные усилия и полученные консультации, отдельные задачи Вы решить не можете, оформите работу, приведя в соответствующих местах ваши попытки решения, изложив коротко соображения и затруднения. Пусть такая работа не будет зачтена, но критические замечания рецензента, его пояснения, ссылки на литературу или письменные консультации по решению конкретных задач помогут Вам найти правильное решение.

5. Если контрольная работа при рецензировании не зачтена, студент обязан представить её на повторную рецензию, включив в неё те задачи, решения которых оказались неверными. Повторная работа представляется вместе с незачтённой.

6. Замечания и рекомендации, сделанные преподавателем кафедры, следует рассматривать как руководство для подготовки к беседе по решению задач. Все тетради с контрольными работами нужно сохранять, так как на экзамен студент допускается только при их предъявлении. Студент должен быть готов во время собеседования или экзамена дать пояснения по существу решения задач, входящих в контрольные работы.

7. Перед решением задачи следует выписать в единицах Си числовые значения используемых при вычислении физических постоянных, а также тех величин, которые даны в условии задачи в единицах, кратных или дольных от единиц Си, а также в единицах, отличных от единиц Си.

8. Решение задач и используемые формулы должны сопровождаться пояснениями. В пояснениях к задаче необходимо указывать те основные законы и формулы, на которых базируется решение данной задачи. Для пояснения решения задачи, где это нужно, аккуратно сделать чертёж.

9. При получении расчётной формулы, которая нужна для решения конкретной задачи, необходимо приводить её вывод.

10. Решение задачи рекомендуется сначала сделать в общем виде, т.е. только в буквенных обозначениях, поясняя применяемые при написании формул буквенные обозначения.

11. Вычисления следует проводить путём подстановки заданных числовых величин в расчётную формулу. При этом студентам рекомендуется делать одну-две промежуточные записи между постановкой и конечным результатом вычислений, несмотря на то, что в примерах решения задач такие записи не приведены.

12. Необходимо проверить единицы полученных величин по расчётной формуле и тем самым подтвердить правильность её. Для этого подставить в неё обозначения единиц, входящих в формулу величин, и, выполнив преобразования, убедиться, что единицы правой и левой частей формулы совпадают.

13. В контрольной работе следует указывать учебники и учебные пособия, которые использовались при решении задач.

14. Контрольные работы, представленные без соблюдения указанных правил, а также работы, выполненные не по своему варианту, зачитываться не будут.