§ 1.6. Системы линейных алгебраических уравнений (с.Л.А.У.). Матричный метод решения, правило Крамера.

Определение. Системой из m линейных алгебраических уравнений с n неизвестными называется система вида:

(1.1)

Здесь переменные x₁,x₂,...,x_n называются неизвестными системы, числа a_ij, где i=1,2,…,m, j=1,2,…,n называются коэффициентами системы, а числа b₁,b₂,...,b_m –свободными членами.

Числа x₁,x₂,...,x_n, обращающие все уравнения системы в тождества, называются решением системы. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Пример1. Система   совместна, так как имеет решение x₁=1, x₂=2.

Система   несовместна.

Имеется более краткая запись С.Л.А.У., она состоит в следующем.

Обозначаем через A матрицу размера mn, составленную из коэффициентов при неизвестных

.

Она называется матрицей системы. Столбец свободных членов обозначим через  , а столбец из неизвестных системы через  . Тогда систему (1.1) можно записать в виде матричного уравнения:

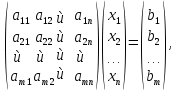
или короче AX=B.

Эта запись называется матричной формой записи системы.

В случае, если матрица A квадратная, матричная форма записи позволяет решить систему с использованием обратной матрицы A^-1.

Теорема. С. Л. А. У.  имеющая квадратную невырожденную

матрицу, имеет единственное решение, которое находится по формуле: X=A^-1B.

Доказательство. Умножим обе части равенства AX=B слева на A^-1, получим A^-1AX=A^-1B, отсюда EX=A^-1B и X=A^-1B.

Метод решения С.Л.А.У. с использованием соотношения X=A^-1B называется матричным методом решения.

Пример2. Решим систему матричным методом.

Матрица этой системы   – невырожденная, A=–3. Найдём обратную матрицу  . Для данной системы  , поэтому  , cледовательно x₁=1, x₂=2.

Данный метод решения систем можно записать и в несколько ином виде, который называется правилом Крамера.

Следствие. Пусть С.Л.А.У. имеет квадратную матрицу A n-го порядка, A=0. Пусть _i – определитель матрицы системы, в которой вместо i-го столбца подставлен столбец свободных членов. Тогда эта система имеет единственное решение, которое находится по формулам   Эти формулы называются формулами Крамера.

Пример3. Решим систему по правилу Крамера.

поэтому: 

§ 1.7. Метод Гаусса для исследования и решения с.Л.А.У.

Матричный метод и правило Крамера обладают двумя существенными недостатками. Во–первых, они применимы только для систем с невырожденной квадратной матрицей и не работают в случае, когда =0. Во–вторых, с ростом n объём вычислений для этих методов слишком быстро возрастает и для n10 они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать метод Гаусса.

Исследовать систему – это значит определить совместна ли она и, в случае совместности, определить, сколько решений она имеет.

Определение. Расширенной матрицей С.Л.А.У. называется матрица, полученная из матрицы системы приписыванием справа столбца свободных членов системы.

Для системы из m уравнений с n неизвестными, она имеет размер m(n+1) и обозначается через  .

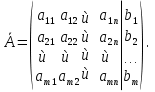
Свободные члены обычно отделяются вертикальной чертой.

Понятно, что ранг   либо равен рангу A, либо превышает его на 1. Следующая теорема позволяет устанавливать факт совместности или несовместности системы.

Теорема Кронекера – Капелли. Система линейных алгебраических уравнений совместна только в том случае, когда ранг её матрицы совпадает с рангом расширенной матрицы (r(A)= r( )).

Если r(A) r( ), то СЛАУ решений не имеет.

Для совместных систем линейных уравнений верны следующие теоремы.

1. Если ранг матрицы совместной системы равен числу неизвестных, т.е. r=n, то система имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа неизвестных, т.е. r<n, то система неопределенная и имеет бесконечное множество решений.

Пусть r<n. r неизвестных   называются базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные n-rназываются свободными.

При решении системы линейных уравнений не нужно отдельно вычислять ранги, а затем их сравнивать. Достаточно сразу применить метод Гаусса.

Преобразования Гаусса удобно проводить, осуществляя преобразования не над самими уравнениями, а над матрицей их коэффициентов.

Достоинства метода Гаусса по сравнению с другими :

• Значительно менее трудоемкий;

• Позволяет однозначно установить, совместна система или нет, а в случае совместности найти её решения (единственное или бесконечное множество);

• Дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.

Пример4.

Исследовать и решить систему

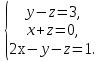
Запишем расширенную матрицу   и приведём её к треугольному виду:

т.к. r( )= r(A)=3 система совместна и имеет единственное решение. По последней матрице восстанавливаем систему и решаем её начиная с последнего уравнения.

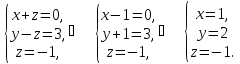
Мы получили, что r(A)=2, r()=3 т.е. r(A) r(). Система решений не имеет.

Пример 5. Исследовать и решить систему 

Запишем и приведем к треугольному виду матрицу  .

Мы получили, что r(A)=2, r()=3 т.е. r(A) r(). Система решений не имеет.

Пример 6. Исследовать и решить систему  .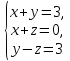

Запишем и приведем к треугольному виду матрицу .

Здесь r(A)=r( )=2<3. Система имеет бесконечно много решений зависящих от 3–2=1 свободного неизвестного  . Задавая свободному неизвестному произвольные значения=с, найдем бесконечное множество решений системы. Восстановим систему по последней матрице и решим её.