Матрицы. Действия над матрицами

Матрицей размерности   называется прямоугольная таблица, состоящая из   элементов, расположенных в m строках и n столбцах.

Элементы матрицы   (первый индекс i − номер строки, второй индекс j − номер столбца) могут быть числами, функциями и т. п. Матрицы обозначают заглавными буквами латинского алфавита.

Матрица называется квадратной, если у нее число строк равно числу столбцов (m = n). В этом случае число n называется порядком матрицы, а сама матрица называется матрицей n-го порядка.

Элементы с одинаковыми индексами   образуют главную диагональ квадратной матрицы, а элементы   (т.е. имеющие сумму индексов, равную n+1) − побочную диагональ.

Единичной матрицей называется квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы равны 0. Она обозначается буквой Е.

Нулевая матрица − это матрица, все элементы которой равны 0. Нулевая матрица может быть любого размера.

К числу линейных операций над матрицами относятся:

1) сложение матриц;

2) умножение матриц на число.

Операция сложения матриц определена только для матриц одинаковой размерности.

Суммой двух матриц А и В называется матрица С, все элементы которой равны суммам соответствующих элементов матриц А и В:

.

Произведением матрицы А на число k называется матрица В, все элементы которой равны соответствующим элементам данной матрицы А, умноженным на число k:

.

Операция умножения матриц вводится для матриц, удовлетворяющих условию: число столбцов первой матрицы равно числу строк второй.

Произведением матрицы А размерности   на матрицу В размерности   называется матрица С размерности  , элемент i-ой строки и j-го столбца которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

.

Произведение матриц (в отличие от произведения действительных чисел) не подчиняется переместительному закону, т.е. в общем случае А В   В А.

1.2. Определители. Свойства определителей

Понятие определителя вводится только для квадратных матриц.

Определителем матрицы 2-го порядка   называется число, вычисляемое по следующему правилу

.

Определителем матрицы 3-го порядка 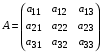  называется число, вычисляемое по следующему правилу:

Первое из слагаемых со знаком «+» представляет собой произведение элементов, расположенных на главной диагонали матрицы ( ). Остальные два содержат элементы, расположенные в вершинах треугольников с основанием, параллельным главной диагонали (  и  ). Со знаком «-» входят произведения элементов побочной диагонали ( ) и элементов, образующих треугольники с основаниями, параллельными этой диагонали (  и  ).

Это правило вычисления определителя 3-го порядка называется правилом треугольников (или правилом Саррюса).

Свойства определителей рассмотрим на примере определителей 3-го порядка.

1. При замене всех строк определителя на столбцы с теми же номерами, что и строки, определитель своего значения не меняет, т.е. строки и столбцы определителя равноправны

.

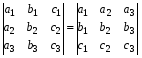2. При перестановке двух строк (столбцов) определитель меняет свой знак.

3. Если все элементы некоторой строки (столбца) нули, то определитель равен 0.

4. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

5. Определитель, содержащий две одинаковые строки (столбца), равен 0.

6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

7. Если каждый элемент некоторого столбца (строки) определителя представляет сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в том же столбце (строке) стоят первые слагаемые, а в другом − вторые. Остальные элементы у обоих определителей одинаковые. Так,

.

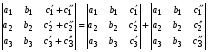8. Определитель не изменится, если к элементам какого-либо его столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число.

Следующее свойство определителя связано с понятиями минора и алгебраического дополнения.

Минором элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, на пересечении которых этот элемент расположен.

Например, минором элемента   определителя   называется определитель  .

Алгебраическим дополнением элемента  определителя называется его минор, умноженный на  , где i − номер строки, j − номер столбца, на пересечении которых находится элемент  . Алгебраическое дополнение обычно обозначается  . Для элемента   определителя 3-го порядка алгебраическое дополнение

9. Определитель равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения.

Например, определитель можно разложить по элементам первой строки

,

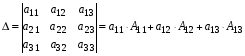или второго столбца

Контрольная работа 2.2. Конспект лекции Лекции № 1-3 Тема 1. Линейная алгебра

§ 1.1. Матрицы. Определители 2-го и 3-го порядков. Свойства

определителей

Определение. Матрицей размера m n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:

. (1)

Числа стоящие в матрице называются ее элементами и обозначаются буквой с двумя индексами, первый из которых равен номеру строки, а второй  номеру столбца в пересечении которых находится данный элемент. Элементы матрицы обычно обозначаются малыми буквами, а сами матрицы  соответствующими заглавными. Если матрица задаётся перечислением своих элементов, то таблица элементов заключается в круглые или квадратные скобки.

Например, матрица a размера 23 записывается в виде:

Эта матрица состоит из 6 элементов  , где i=1,2 – есть номер строки, j=1,2,3 – номер столбца. Матрицы используются в технических науках и в экономике для записи табличной информации. В программировании матрицы называются двумерными массивами.

Матрица у которой число строк равно числу столбцов называется квадратной, а число строк (столбцов) этой квадратной матрицы называется ее порядком. Квадратная матрица n– го порядка состоит из n² элементов:

. (2)

Каждой квадратной матрице по определённому правилу сопоставляется число, которое называется определителем этой матрицы. Определитель, в отличие от матрицы обозначается вертикальными линиями:

.

Сформулируем правила вычисления определителей 1-го, 2-го, 3-го порядков.

1. Определителем матрицы 2-го порядка называется число

.

Например:

.

2. Определителем матрицы 3-го порядка называется число

.

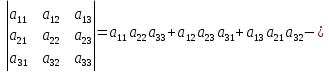
Это правило называется правилом треугольников (Саррюса). Для его запоминания используется следующая схематическая запись, где элементы, расположенные на месте черных точек перемножаются:

Например:

Определение: Транспонированной матрицей для матрицы A называется матрица A^T, столбцами которой являются соответствующие строки матрицы A.Диагональ, исходящая из левого верхнего угла матрицы, называется её главной диагональю. Для квадратной матрицы (2) транспонированная матрица записывается так:

Рассмотрим теперь свойства определителей, справедливые для определителей любого порядка. Для определённости будем их записывать для определителей 3-го порядка.

І. Определители квадратной матрицы A и её транспонированной A^T совпадают, т.е. |A|=|A^T|.

Дальнейшие свойства определителей мы будем формулировать для его строк. Из первого свойства следует, что все они справедливы и для столбцов.

ІІ. При перемене местами двух строк матрицы, её определитель меняет свой знак на противоположный.

Например:

.

В определителе поменяли местами вторую и третью строки.

ІІІ. Определитель матрицы с двумя одинаковыми строками равен 0.

В самом деле, при перемене местами этих строк, согласно свойству 2, определитель должен удовлетворять уравнению  . Отсюда,  , следовательно  .

ІV. Если все элементы одной строки квадратной матрицы умножить на число , то её определитель умножится на это число.

Например:  .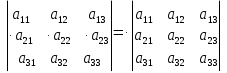

V. Если квадратная матрица содержит нулевую строку, то её определитель равен 0.

Это свойство получается из предыдущего при =0.

VІ. Если одна из строк определителя записывается в виде суммы двух строк, то определитель записывается в виде суммы двух определителей у которых на месте этой строки стоят соответственно первые и вторые слагаемые. Остальные соответствующие строки всех трёх определителей равны.

Например:

VІІ. Если к одной строке матрицы прибавить другую её строку, умноженную на число , то определитель матрицы при этом не изменится.

Например:

.