
- •1 . Введение в теорию направленных отношений предисловие
- •Введение в теорию направленных отношений.
- •Основные понятия.
- •Языки схем -отношений.
- •Классы -отношений.
- •Операции композиции -отношений.
- •Комбинаторные -отношения.
- •Дефинициональные расширения.
- •Конструктивные -отношения.
- •Основные результаты. Вначале докажем теорему о комбинаторной полноте .
- •Иерархия классов -отношений.
- •Исчисления включения и эквивалентности схем -отношений.
- •Отношения включения и эквивалентности схем -отношений.Рассмотрим схемы -отношенийиодной и той же арности.
- •Бестиповые направленные отношения.
- •Сигнатуры языков схем бестиповых-отношений.
- •Представление типизированных рекурсивных схем бестиповыми регулярными схемами.
- •Вычислительная полнота множества констант языка бестиповых регулярных схем -отношений основной универсальной сигнатуры.
- •Литература
- •Оглавление
- •12. Бестиповые направленные отношения. 33
- •51 F logol: язык и система функционально-логического программирования
Исчисления включения и эквивалентности схем -отношений.
В этом разделе мы
рассмотрим формализацию таких
фундаментальных взаимных свойств
![]() -отношений,
каквключение
и эквивалентность.
-отношений,
каквключение
и эквивалентность.
Отношения включения и эквивалентности схем -отношений.Рассмотрим схемы -отношенийиодной и той же арности.
Определение
1.9. Схема
![]() -отношений
-отношений![]() включает
схему
включает
схему
![]() -отношений
-отношений![]() в интерпретации
в интерпретации![]() ,
если
,
если![]()
![]()
![]()
![]() .
Схема
.
Схема
![]() -отношений
-отношений![]() эквивалентна
схеме
эквивалентна
схеме
![]() -отношений
-отношений![]() в интерпретации
в интерпретации ![]() ,
если
,
если![]()
![]()
![]()
![]()
![]() .
.
Определение
1.10. Схема
![]() включает
схему
включает
схему
![]() в сильном
смысле,
если
в сильном
смысле,
если
![]()
![]()
![]()
![]()
для любой интерпретации
для любой интерпретации
![]() переменных. Схема
переменных. Схема![]() эквивалентна
схеме
эквивалентна
схеме
![]() в сильном
смысле, если
в сильном
смысле, если
![]()
![]()
![]()
![]()
для любой интерпретации
для любой интерпретации
![]() переменных.
переменных.
Очевидно, отношение
эквивалентности схем
![]() и
и![]() выполняется, если выполняются отношения
включения между
выполняется, если выполняются отношения
включения между![]() и
и![]() в обе стороны. Отношения сильного
включения и эквивалентности будем
обозначать через
в обе стороны. Отношения сильного
включения и эквивалентности будем
обозначать через![]() и
и![]() , соответственно.
, соответственно.
Исчисление сильного включения ациклических схем
 -отношений.
Ниже приведены аксиомы и правила вывода
исчисления сильного включения, сокращенно
обозначенного
-отношений.
Ниже приведены аксиомы и правила вывода
исчисления сильного включения, сокращенно
обозначенного
 (
( ),
для языка
),
для языка ациклических схем
ациклических схем -отношений.
-отношений.
В этом исчислении
![]() ,
,![]() ,
,![]() ,
возможно, с индексами, обозначают
произвольные схемы
,
возможно, с индексами, обозначают
произвольные схемы![]() -отношений.
Запись
-отношений.
Запись![]() есть сокращение для пары схем аксиом
есть сокращение для пары схем аксиом![]() и
и![]() .
Там, где не указаны арности схем
.
Там, где не указаны арности схем![]() -отношений,
предполагается, что они могут быть
любыми, при условии, что соблюдается
правильность согласования арностей
при построении соответствующих схем и
формул исчисления.
-отношений,
предполагается, что они могут быть
любыми, при условии, что соблюдается
правильность согласования арностей
при построении соответствующих схем и
формул исчисления.
Схемы аксиом :
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
..

 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
Правила вывода:
П1.
![]()
П2.
![]()
Здесь
![]() – результат замены в схеме
– результат замены в схеме![]() некоторого вхождения схемы
некоторого вхождения схемы![]() на схему
на схему![]() .
.
Истинность аксиом и непротиворечивость правил вывода поддаются непосредственной проверке.
Теорема
1.11 . Исчисление
![]() полно на множестве схем
полно на множестве схем![]() -отношений
языка
-отношений
языка![]() (т.е.
(т.е.![]()
![]()
![]()
![]()
![]()
) для всех схем
) для всех схем
![]()
![]() .
Доказательство этой теоремы будет дано
в главе 2 (после введения сетевого
представления схем
.
Доказательство этой теоремы будет дано
в главе 2 (после введения сетевого
представления схем![]() -отношений).
-отношений).
Отношение включения рекурсивных схем
 -отношений.
При формализации отношения включения
для схем
-отношений.
При формализации отношения включения
для схем
 -отношений
языка
-отношений
языка ,
т.е. построенных с использованием
оператора наименьшей фиксированной
точки, исчисление
,
т.е. построенных с использованием
оператора наименьшей фиксированной
точки, исчисление расширяется добавлением аксиомы
фиксированной точки и правила индукции:
расширяется добавлением аксиомы
фиксированной точки и правила индукции:
 (аксиома
фиксированной точки),
(аксиома
фиксированной точки),
П3.
 (правило
индукции),
(правило
индукции),
где
![]() – формула исчисления (т.е. формула вида
– формула исчисления (т.е. формула вида![]() или
или![]() ),
),![]() – множество формул-посылок, не содержащих
свободных вхождений переменной
– множество формул-посылок, не содержащих
свободных вхождений переменной![]() .
.
Однако, добавление
этой аксиомы и правила вывода по индукции,
несмотря на их теоретическую оправданность
и практическую полезность, не приводит
к построению исчисления включения
![]() -отношений,
обладающего статусом полноты, что
справедливо для
-отношений,
обладающего статусом полноты, что
справедливо для![]() .
Более того, множество истинных формул
сильного включения для класса рекурсивных
схем
.
Более того, множество истинных формул
сильного включения для класса рекурсивных
схем![]() -отношений
не является рекурсивно-перечислимым.
-отношений
не является рекурсивно-перечислимым.
Отношение сильного включения схем конструктивных
 -отношений.
Множество элементарных констант в
языках схем конструктивных
-отношений.
Множество элементарных констант в
языках схем конструктивных
 -отношений
состоят из символов
-отношений
состоят из символов конструкторов и символов деструкторов
конструкторов и символов деструкторов .
Комбинаторные константы вводятся по
определению.
.
Комбинаторные константы вводятся по
определению.
Исчисление включения
для схем конструктивных
![]() -отношений
содержит аксиомы 1¸8,
18¸31
и аксиомы, определяющие свойства
конструкторов:
-отношений
содержит аксиомы 1¸8,
18¸31
и аксиомы, определяющие свойства
конструкторов:
 , для всех
, для всех
 .
. ,
для всех
,
для всех
 и
и .
. .
.
К правилам вывода присоединяется правило П4 вывода по контексту:

Нижеследующие
утверждения (выводимые в этом исчислении)
раскрывают другие важные свойства
конструкторов
![]() ,
,![]()
 (функциональность
конструктора
(функциональность
конструктора
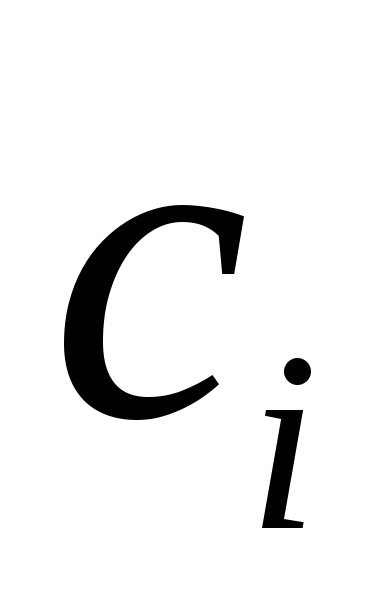 ),
), (функциональность
деструктора
(функциональность
деструктора
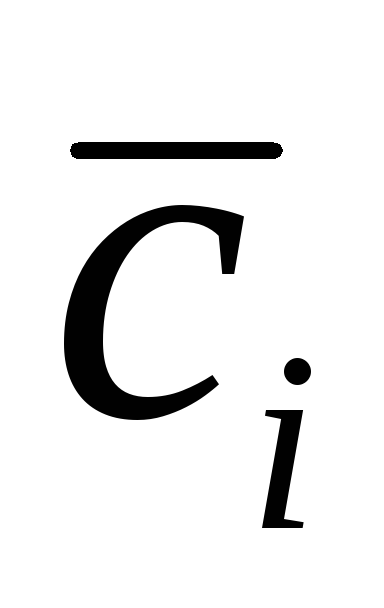 ),
), (тотальность
конструктора
(тотальность
конструктора
 ),
), ,
,
 (неунифицируемость
различных конструкторов).
(неунифицируемость
различных конструкторов).
В практическом
плане для доказательства включения
схем конструктивных
![]() -отношений,
вероятно, более полезным является другое
правило индукции, которое выводимо из
выше сформулированного
правила П3:
-отношений,
вероятно, более полезным является другое
правило индукции, которое выводимо из
выше сформулированного
правила П3:
П5.![]() ,
,
где
![]() ,
,
![]() ,
а
,
а![]() не входит свободно в
не входит свободно в![]() .
.
