4. Классы -отношений.

Пару назовемсигнатурой языка схем -отношений. Язык с сигнатуройбудем обозначатьили, в зависимости от того, используется или нет при его построении оператор рекурсии.

Множество свободных переменных схемы определяется обычным образом:

для всех ;

для всех ;

для всех ;

.

Схема, множество свободных переменных которой пусто, называется константой языка. Обозначим через множество-отношений – денотатов констант языка.

Пусть – подмножество-отношений из, которые могут выступать в качестве интерпретантов переменных языка().

Определение 1.5 .

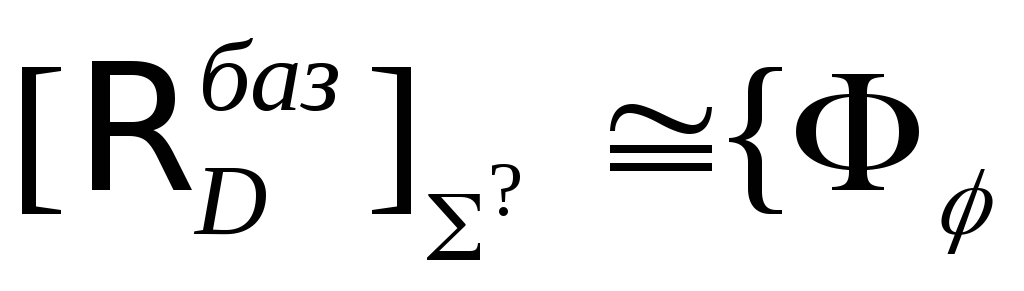
–класс -отношений, порожденных изязыком.

Как следствие этого определения, получим, что

.

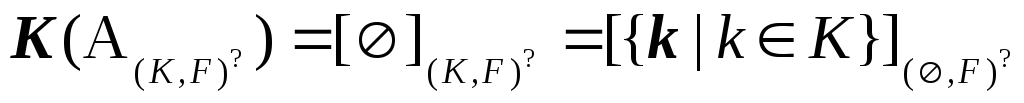Далее рассматриваются различные сигнатуры языков схем отношений и особенности классов -отношений, порождаемых этими языками. Основное внимание будет уделено cигнатурам, в определенном смысле не зависящим от выбора конкретного носителя(некоторую роль будет играть только мощность множества). Более того, мы вообще ограничимся рассмотрением только наборов связок, отвечающих этому требованию: любая перестановкана носителедля присоединенных функций связок является автоморфизмом, то есть длясправедливо утверждение

, где распространяется на-отношения общепринятым образом. Константы, удовлетворяющие условию независимости от выбора носителя, назовемкомбинаторными, и посвятим им отдельный параграф. В дальнейшем будут рассмотрены и языки, сигнатура которых связана со спецификой носителя, а именно, когда в качестве носителя рассматривается эрбрановский универсум.

5. Операции композиции -отношений.

Операция последовательной композиции -отношений. Последовательная композиция -отношенийиобозначается черези определяется как произведение графикови:

Если и–-отношения арностейи, соответственно, то–-отношение арности. Операция последовательной композиции ассоциативна.

Операция параллельной композиции -отношений. Параллельная композиция -отношенийиобозначается черези определяется как раздельное декартово произведение компонентов графикови:

Если и– типизированные-отношения арностии, то–-отношение арности. Операция параллельной композиции ассоциативна.

Операция объединения -отношений. Объединение -отношенийиобозначается черези определяется как теоретико-множественное объединение-отношенийикак графиков.

Для объединения требуется равенство арностей -отношенийи, причем результат объединения будет иметь ту же самую арность. Операция объединения ассоциативна и коммутативна.

Операция пересечения -отношений. Пересечение -отношенийиобозначается черези определяется как теоретико-множественное пересечение-отношенийикак графиков.

Для пересечения также требуется равенство арностей -отношенийи, причем результат пересечения имеет ту же самую арность. Операция пересечения ассоциативна и коммутативна.

Операция конкатенации. Конкатенация -отношенийиопределяется как декартово произведение вторых компонентов графиков при равных первых компонентах:

Конкатенация определена только для операндов арностей и, соответственно. Результат операции будет иметь арность.

Операция эквализации (унификации). Эквализация -отношенийиопределяется как декартово произведение первых компонентов графиков при равных вторых компонентах:

Эквализация определена только для операндов арностей и. Результат операции будет иметь арность.

Условная композиция. Условная композиция -отношенийиобозначается знакоми представляет собой проекциюпо первому компоненту графика на область определения-отношения:

Арности операндов условной композиции должны быть и, соответственно. Результат композиции, очевидно, имеет арность второго операнда.

Операция итерации. Итерация -отношенияобозначаетсяи определяется так:

, где (тождественное-отношение арности),и.³

Очевидно, что итерация -отношенияявляется наименьшим решением уравнения, т.е..

Результат применения итерации будет иметь ту же арность , что и ее операнд.

Операция повторения. Повторение -отношенияобозначаетсяи определяется так:

.

Результат применения операции повторения будет иметь ту же арность , что и ее операнд.

В заключение этого параграфа покажем эквивалентность задания рекурсивных схем с использованием оператора рекурсии и в форме системы уравнений.

Пусть – рекурсивная схема -отношений. Произведем переименование операторных переменных в так, что для всех операторов они будут попарно различны и не будут совпадать со свободными переменными схемы . Не ограничивая общности, будем считать, что входящие в операторы имеют вид . Полагая , преобразуем к эквивалентной форме задания в виде конечной системы уравнений вида , такой, что – результат замены в каждого внешнего (т.е. не являющегося частью другого входящего в оператора) вхождения в нее оператора на соответствующую операторную переменную. Очевидно, что для любой интерпретациисвободных переменных значение переменнойв минимальном решении этой системы уравнений в интерпретацииесть.

Пусть, наоборот, теперь задана система уравнений вида ,где переменнаяпредставляет интересующую нас схему -отношений, причем в правых частях уравнений не используется оператор рекурсии. Полагая, что, последовательно, для всех, осуществим исключение из системы-х уравнений: каждая новая система уравнений будет иметь вид,, где(результат подстановки схемыв правые части первыхуравнений системы вместо всех вхождений переменной). Наконец, искомую рекурсивную схему определим как .