6. Комбинаторные -отношения.

Определение 1.6 . -отношениеназываетсякомбинаторным, если оно является фиксированной точкой для любой перестановки на носителе:для любого всюду определенного навзаимно-однозначного отображения. Класс комбинаторных-отношений на носителеобозначим, полагая, что сам носитель ясен из контекста (фактически нас интересует только его мощность).

Теорема 1.1. Всякое комбинаторное -отношениеарностиопределяется множествомпар, где– некоторое отношение эквивалентности на множествеиндексов, а– множество ребер графа на факторе множествапо отношению():

Пустое множество задает пустое комбинаторное-отношение. Комбинаторное-отношение, индуцированное одноэлементным множеством, назовем простым. Класс простых комбинаторных-отношений наобозначим.

Среди простых комбинаторных -отношений особо выделим следующие-отношения⁴:

1) тождественные -арные,,-отношения. Очевидно, что – правая и левая единица операции последовательной композиции -отношений: ;

2) . – правая и левая единица операции параллельной композиции: ;

3) пустые -арные-отношения,обозначаются . – правые и левые единицы для операции объединения -отношений:

;

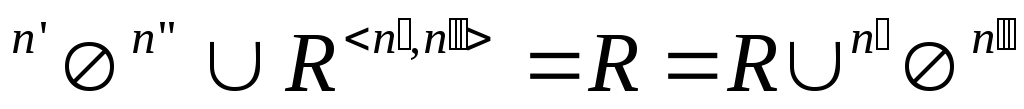4) универсальные -арные-отношения,обозначаются . – правые и левые единицы для операции пересечения -отношений:

.

Теорема 1.2. Количество различных комбинаторных -отношений конечно для любой арности,.

Выделим в множестве простых комбинаторных -отношений следующее подмножествоэлементарных-отношений:

⁵,

где ,

,

,

,

,

.

Теорема 1.3. , где.

Теорема 1.4. , где.

Комбинаторные -отношения изявляются независимыми по операциям последовательной и параллельной композиции, если не ставится никаких ограничений на мощностьносителя. Однако, например, прикласс-отношений навключает только  и пустые -отношения для всех , и поэтому , , , , , . Напротив, для не является независимой константой: . Константа эквивалентна для ,  для и (см.1.6) для .

7. Дефинициональные расширения.

Согласно теоремам 1.3 и 1.4 мы можем вводить в рассмотрение любые комбинаторные -отношения путем задания их по определению. Покажем, например, каким образом через элементарные комбинаторные-отношения изс помощью операций композиции могут быть определены аналогичные им комбинаторные-отношения любой арности,

Пусть . Определим сначала тождественное-арное-отношение : a) , b) , где .

-Отношения и определим так:

, , .

Универсальное -арное-отношение  определяется так: .

Остальные константы:

,

,

,

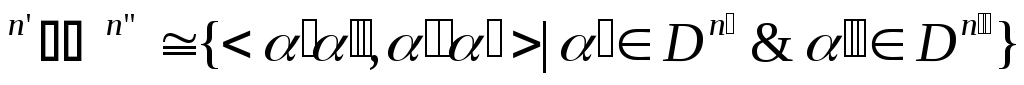
могут быть определены следующим образом:

1) , ,

;

2) , ,

3) , ,

4) , .

Нижеследующее дефинициональное расширение определяет -арное комбинаторное-отношение выделения-го компонента кортежа:

.

Обратное ему отношение обозначается так: .

Константа , , («пустое» -отношение арности) определяется через пустое-арное-отношение : , причем может быть выражено как минимальное решение уравнения , гдеимеет арность. может быть выражено и без применения оператора рекурсии:  для пустого носителя и , в противном случае.

8. Основные сигнатуры.

   Помимо сигнатуры , определим также какосновные: сигнатуру , и производные от них сигнатурыи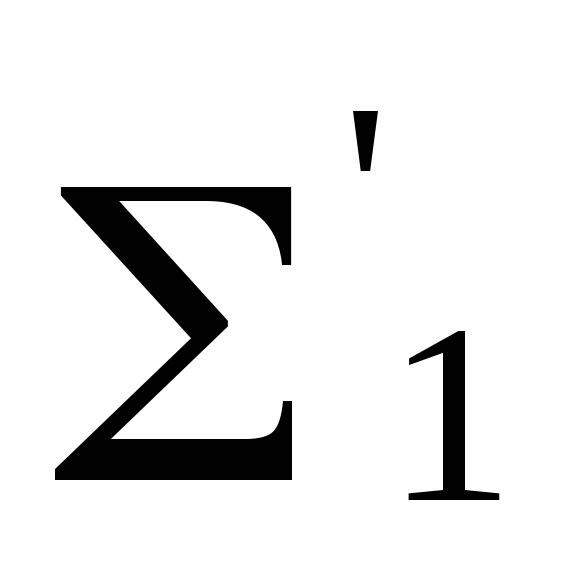, полученные исключением константы  и добавлением константы к и, если в соответствующем языке не используется оператор рекурсии.

Теорема 1.5 .идля.

Доказательство:

1. Переход от к:

a) очевидно, что для любых -отношений,(здесь и далееможет использоваться при изображении комбинаторных констант для обозначения произвольного необходимого по контексту натурального числа. Например, в данном случае уточнение могло быть таким: );

b) константа выражается в так: . Таким образом, все компоненты сигнатуры выразимы в.

2. Переход от к:

,

,

.

Для сигнатур идоказательство аналогично. Теорема доказана.

Основные сигнатуры в определенном смысле полны (с учетом сформулированных ранее ограничений и возможности использования оператора рекурсии), что позволяет, в частности, выразить в них и другие введенные нами операции композиции -отношений:

,

,

,

.

Теорема 1.6.

.

Доказательство осуществляется определением отображения , применяемого к схемам индукцией по синтаксической сложности. Пусть– взаимно-однозначное отображение на множестве переменных, такое, что для всехарноститоже имеет арность:

1) для базисных комбинаторных констант сигнатуры :

, ,,

, ,,

2) ,

3) ,

4) ,

5) ,

6) .

Очевидно, что для всякого  , где для всех . Применяя те же построения в обратную сторону, получим доказательство теоремы.