1 . Введение в теорию направленных отношений предисловие

Предлагаемая вниманию читателей серия изданий посвящена проблемам создания языков и систем программирования высокого уровня непроцедурного типа. Известно, что для решения многих задач, для которых не создано эффективных алгоритмов, применение методов рекурсивного функционального программирования в сочетании со средствами логического вывода является не только удобной, но порой и единственной возможностью. Основными недостатками большинства известных языков непроцедурного программирования является их низкий, в современном понимании, уровень и, как правило, невозможность органичного сочетания методов функционального и логического подходов, как в постановке задач, так и при организации вычислительного процесса. Представленные материалы знакомят читателей с основами оригинальной теории направленных отношений [1-4,6-7](Фальк В.Н., Кутепов В.П.), как единой основы для реализации функционального, логического и реляционного подхода к решению задач, с основными принципами построения языка непроцедурного программирования высокого уровня FLOGOL [5] (Фальк В.Н.), а также с особенностями организации системы функционально-логического программирования S-FLOGOL [8-9] (Фальк В.Н., Бебчик Ал.Н., Бебчик Ан.Н.), включающей новые технологические и программные средства поддержки как разработки, так и исполнения функционально-логических программ. В дальнейшем предполагается дополнить издание разделами, посвященными другим приложениям теории направленных отношений – описанию денотационной семантики и верификации операторных схем программ, проблемам связи со структурной теорией графов и др., а также перспективам реализации системы функционально-логического программирования на современных вычислительных средствах с развитым параллелизмом при организации вычислительного процесса.

1. Введение в теорию направленных отношений.

1. Основные понятия.

Определение 1.1. Направленным отношением (или, сокращенно, -отношением) арности на множестве (носителе) называется график соответствия изв.

Здесь – множество всевозможных кортежей элементов множествадлины. Иными словами, направленное отношениеарностина носителе(точнее, его график) есть множество упорядоченных пар вида, где все. Кортежназовемвходным, а кортеж –выходным для соответствующего элемента -отношения. Кортеж нулевой длины (пустой кортеж) обозначается, а в случаях его использования в выражениях там, где это не приводит к недоразумениям, он представляется непосредственно пустым словом.

Арность -отношения, при необходимости, будет указываться в виде правого верхнего индекса.

2. Свойства -отношений.

   Многие виды семантических объектов в конструктивной математике вообще и в теории программирования, в частности, могут рассматриваться как специальные подклассы направленных отношений, различающиеся как арностью 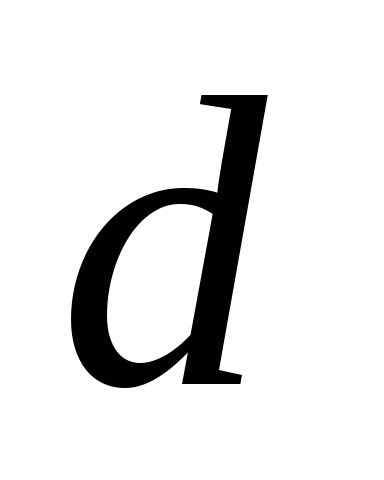-отношений, так и наличием у них особых свойств. В качестве основных таких свойств рассмотрим свойства тотальности и функциональности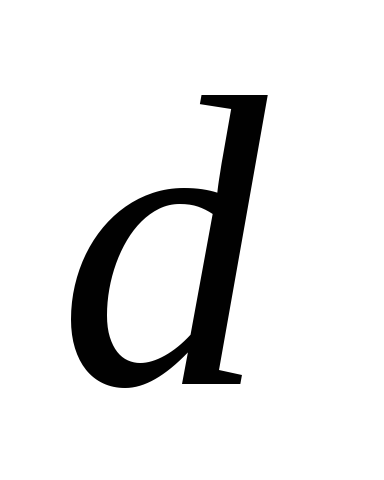-отношений.

Определение 1.2.

-Отношение наназываетсятотальным, если

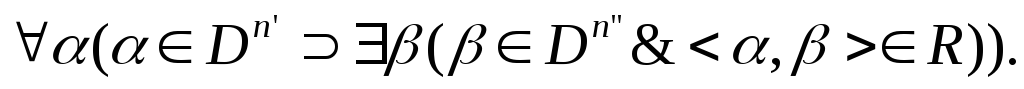
Определение 1.3.

-Отношение наназываетсяфункциональным, если

.

В таблице 1.1 дана классификация типизированных -отношений в зависимости от их арностей, наличия у них свойств функциональности () и тоталь-

ности (), а также наличия этих свойств у обратных им отношений.

Определение 1.4. -Отношениеназываетсяобратным -отно-шению, если¹

Таблица 1.1

-Отношение	Арность,
\Утверждение				2
Объект		+
Множество объектов
Кортеж		+
Множество кортежей
Свойство объекта
Предикат
Перестановка		+	+	+	+
Вложение		+	+	+
Подстановка (тотальная)		+	+
Частичная подстановка		+
Переход
Суперконструктор		+	+	+	+
Конструктор		+	+	+
Функция (тотальная)		+	+
Частичная функция		+
Суперреконструктор		+	+	+	+
Реконструктор		+	+	+
Отображение (тотальное)		+	+
Частичное отображение		+

Заметим, что существуют всего два «логических» -отношения арности: пустое (пустое подмножество пар пустых кортежей) и– множество, содержащее единственный элемент (пару пустых кортежей), которые в приложениях теории направленных отношений играют роль истинностных значенийи, соответственно.