1.5 Бос электрондық жуықтау арқылы энергетикалық зонаны анықтау

Электронның күйын анықтауда кристалдың нүктелік симметриясы қалай қолданатынын нақты мысалдармен көрсетейік. Қарапайым кубтық кристалды қарастырайық. Нөлдік жуықтауда периодты кристалдық потенциал 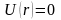болсын дейік, яғни тор бос деп есептелсін. Бос тордағы оң иондардың зарядтары кристалл ішінде біркелкі жайылған деуге болады. болған жағдайда Шредингер теңдеуінің шешімі, Блох шартын қанағаттандыратын жазық толқын түрінде болады.

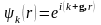. (.22)

Энергияның меншікті мәндері 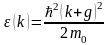, немесе

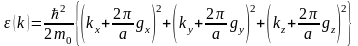. (1.23)

Бұл жердегі 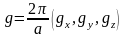− кері тордың трансляция векторы, а – тор тұрақтысы.

Б риллюэн зонасының белгілі бір симметриялы k нүктесі үшін бірнеше g трансляция векторлары табылады және k+g нүктесі бастапқы k нүктесімен эквивалентті болады. Ол нүктелер энергияның бірдей мәндеріне сәйкес келеді. Сондықтан берілген нүктенің симметриясына сәйкес келетіндей етіп, функцияларынан комбинация құру керек.

Бриллюэн зонасының [001] бағытын-дағы функциясының түрін анықтайық. Тор тұрақтысы 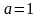болсын. Бұл бағыттағы симметрия сызығы бойында жатқан нүкте-лердің координаттары, 1.5 сурет бойынша , , .

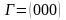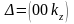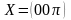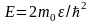белгілеуін енгізіп, бұл нүкте-лердегі энергия мәндерін (4.23) бойынша анықтаймыз.

,

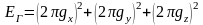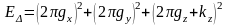, (1.24)

.

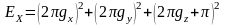Энергияның ең кіші мәні зонаның центріндегі Г нүктесінде, 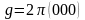болғанда байқалады. Бұл кезде толқындық функция тұрақты болады, ал энергетикалық күйлер Г₁ типке жатады. шартын сақтай отырып, Г нүктесінен Δ сызығы бойымен Х нүктесіне қарай жылжыған кезде энергия мен толқындық функция былай анықталады:

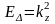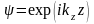, . (1.25)

Δ сызығының соңғы Х нүктесінде

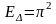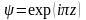, . (1.25)

Энергияның мәніне толқындық векторы 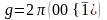болатын, 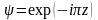функциясы да сәйкес келеді. Соңғы екі функцияның сызықты комбинациясынан Х₁, және типті симметриясы болатын функциялар құрастыруға болады.

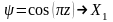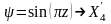; . (1.26)

Х нүктесінде 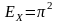болып, одан ары қарай Δ-ның бағытында екінші энергетикалық зона басталады. Бұл нүктеде сақталады және (1.24) бойынша:

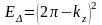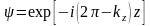; . (1.27)

Екінші зона да, бірінші сияқты Δ₁ типті болады (1.7 сурет). Δ-ның кері бағытындағы Г нүктесінде 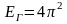болады. Бұл энергияға кері кеңістіктегі трансляция векторының алты түрі сәйкес келеді:

: , , , , , .

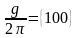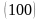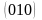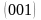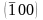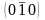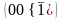Сондықтан, 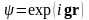тәрізді алты функциядан, берілген нүктенің симметриясына сәйкес сызықты комбинациялар түзіледі. Бұл функция-лардың симметриясы 4.4 кесте бойынша анықталады.

,

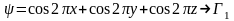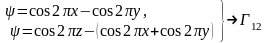, (1.28)

.

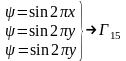нүктесінен бастап ары қарай Δ өсінің бойымен жылжығанда жиынының алты векторына алты түрлі энергетикалық зона сәйкес келеді. Ол зоналардың энергиялары былай анықталады:

; , , , ,

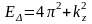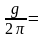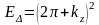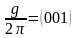; , (1.29)

;

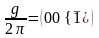
Соңғы энергетикалық зонаға сәйкес функцияны жоғарыда (1.27) бойынша анықтағанбыз. Осыған ұқсас, векторына сәйкес зонасының толқындық функциясын

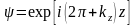
түрде жазамыз және бұл зона да Δ₁ өрнектеуі бойынша түрленеді. Суретте Δ₁ өрнектеуі тұсындағы жақша ішіндегі 1 саны бұл өрнектеудің азғындамаға-нын көрсетеді.

энергиясына сәйкес төрт қайтара азғындаған күйлердің толқындық функцияларын анықтау үшін, (1.22) функциясындағы g векторының оның төрт мәнін қоямыз және 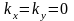деп аламыз. Осылай анықталған төрт экспонентадан сызықты комбинациялар жасалып, 1.6 және 1.7 кестелер бойынша Δ типті симметриялы болатын мына функциялар жазылады:

,

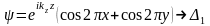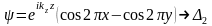, (1.30)

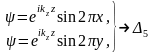
Ары қарай, Δ өсінің бойымен Х нүктесіне қарай жылжығанда, (1.24) бойынша 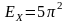. Бұл энергияға кері кеңістіктегі трансляция векторының сегіз түрі сәйкес келеді:

: , , , , , , , .

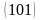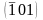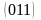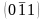Сондықтан Х нүктесінің симметриясына сәйкес келетін толқындық функциялар төмендегі жазық толқындардың комбинациясы арқылы анықталады:

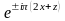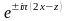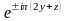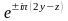, , , . (1.31)

Бұл функциялардың сызықты комбинациялары арқылы Х нүктесіндегі толқындық функциялар анықталады:

,

,

,

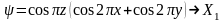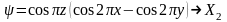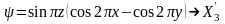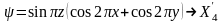, (1.32)

,

.

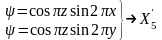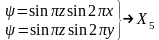1.7 суреттегі энергетикалық зоналар қисығы тұсында жақша ішінде көрсетілген сандар азғындау ретін білдіреді. Мысалы, , 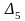, 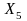өрнектеулері екі өлшемді, яғни Бриллюэн зонасының кейбір симметриялы нүктелерінде Гамильтон операторының бір меншікті мәніне, екі өлшемді өрнектеу арқылы түрленетін, екі толқындық функция сәйкес келеді. Осы сияқты азғындаулар – маңызды азғындаулар деп аталады, себебі олар кристалдың симметриясына байланысты пайда болды. Бұлардан бөлек, Бриллюэн зонасының кейбір нүктелерінде кездейсоқ азғындаулар болуы мүмкін. Мысалы, әртүрлі энергетикалық зоналар қисығы зонаның бір нүктесінде қиылысса, сол нүктеде екі түрлі өрнектеулердің энергиялары тең болады. Бірақ кездейсоқ азғындау ықтималдығы өте аз.