1.3 Топтарды өрнектеу

Өткен тақырыпта геометриялық түрлендірулерге қатысты топтар қарастырылды. Енді ол түрлендірулерді математикалық тұрғыда берілген операторлар ретінде қабылдайық. G қандай-да бір g-ретті симметрия тобы болсын және оның элементтерін жалпылама түрде G деп белгілейік. Сонымен бірге кез келген 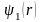функциясы берілсін. 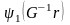Координат жүйесін топтың G элементіне сәйкес түрлендірсек, функциясының аргументі түрленіп, жаңа функциясы шығады. Осылайша, топтың барлық элементтері арқылы түрлендірулер жасалса, жаңа g функциялар жиыны алынады. Бұндай түрлендірулерді оператор арқылы жазамыз:

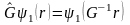. (1.12)

Түрлендірулер нәтижесінде алынған g функцияның барлығы бірдей сызықты тәуелсіз болмауы мүмкін. Олардың ішіндегі f функциялар өзара сызықты тәуелсіз болсын, сонда шыққан функцияларды, тәуелсіз функция-лардың сызықты комбинациясы түрінде жазуға болады.

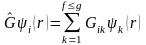. (1.13)

Жіктеудің тұрақты 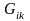коэффициенттер жиыны, G түрлендіру матрица-сының матрицалық элементтері болып табылады. Егер 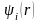функциялары, өзара ортогональ және нормаланған функциялардың толық жүйесі болса, түрлендіру матрицасы, кванттық механикада белгілі, операторға сәйкес матрица болады.

.

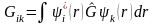Топтың G және H элементтерінің көбейтіндісіне сәйкес матрицалық элемент, матрицаларды көбейту ережесі бойынша анықталады.

.

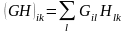Топтың барлық элементтеріне сәйкес матрицалар жиыны топтың өрнектелуі болып табылады, ал осы матрицаларды анықтау үшін алынған 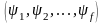тәуелсіз функциялар жүйесі – өрнектеудің базисі деп аталады. Тәуелсіз функциялар саны f, өрнектеудің өлшемі болады. Базистік функцияларды түрлендіру арқылы, бір өрнектеудің орнына екінші өрнектеу алынса, бұл екі өрнектеу өзара эквивалентті болады. G элементіне сәйкес матрицаның ізі (матрицаның бас диагональ элементтерінің қосындысы) – матрицаның сипаты (характері) деп аталады. Эквиавлентті матрицалардың сипаттары бірдей, ал эквивалентті емес матрицалардың сипаттары әртүрлі болады. Сипаттарына қарап, өрнектеулердің эквиваленті, немесе эквивалент-ті емес екендігін ажыратуға болады.

Кандай-да бір сызықты түрлендіру арқылы базис ретінде алынған f функциялар бірнеше бөлікке (топтарға) бөлінген болсын. Бір бөліктегі функцияларға симметриялық түрлендіру тобының кез келген элементі арқылы әсер еткен кезде сол бөліктің функциясы шығатын болса, берілген топтың өрнектелуін сипаттайтын матрицалар жиыны – келтірілетін өрнектеу деп аталады, ал егер базистік функцияларда ешқандай сызықты түрлендіру арқылы бөліктерге бөлуге болмайтын болса, матрицалар жиыны – келтірілмейтін өрнектеу деп аталады. Кез келген келтірілетін өрнектеуді, бірнеше келтірілмейтін өрнектеулерге жіктеуге болады. Әрбір келтірілмейтін өрнектеу үшін, берілген базис ішінен таңдап алынған функциялардың бір бөлігі сәйкес келеді.

Келтірілмейтін өрнектеудегі бір класқа тиісті элементтердің барлығы-ның сипаттары бірдей болады, сондықтан берілген элементтің сипаты оның қай класқа тиісті екенін көрсетеді. Матрицаларды унитар түрлендіруден олардың ізі (сипаты) өзгермейді. Келтірілетін өрнектеудің матрицасын унитар түрлендіру арқылы блокты диагональ түрге келтіруге болады [17].

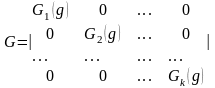(1.14)

Диагональда орналасқан блок түріндегі әрбір матрица, келтірілмейтін өрнектеуге сәйкес келеді және олардың өздерінің сипаттары болады. Үлкен матрицаның диагональ элементтерінің қосындысы, блок түріндегі жеке матрицалардың диагональ элементтерінің қосындысына тең. Олай болса, кез келген келтірілетін өрнектеудің сипаты, сол өрнектеу ішіндегі келтірілмейтін өрнектеулердің сипаттрының қосындысына тең.

Берілген кванттық жүйенің (атомның, кристалдың) симметриясына сәйкес координат жүйесін түрлендіргеннен, оны сипаттайтын Шредингер теңдеуінің түрі өзгермейді. Олай болса, симметриялы түрлендірулерді, берілген энергияға сәйкес Шредингер теңдеуінің шешімі болатын толқындық функцияға қолданғанда шығатын функция, сол энергияға сәйкес күйді білдіреді. Берілген энергетикалық деңгейге сәйкес толқындық функцияларға симметриялы түрлендірулер жасағанда, сол энергияны сипаттайтын басқа толқындық функциялар алынады. Сондықтан симметрия топтары ішінде, әрбір энергетикалық деңгейге сәйкес келетін, келтірілмейтін өрнектеу топтары болады (Вигнер теоремасы).

Топтар теориясын физикалық жүйелерге қолдануда келтірілмейтін өректеулер маңызды роль атқарады. Бірдей келтірілмейтін өрнектеу арқылы түрленетін толқындық функциялар энергияның бір меншікті мәніне сәйкес келеді. Сондықтан келтірілмейтін өрнектеулердің өлшемі берілген кванттық күйдің азғындау дәрежесін білдіреді.

Электронның спинін ескерген кездегі толқындық функциясын симметриялы түрлендіруге тоқталайық. Электронның спиндік моментінің кез келген өстегі проециясы 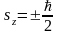екі мәнді қабылдайды. Сондықтан оның толқындық функциясын екі құраушыдан тұрады.

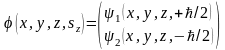. (1.15)

Егер электронның спині оның координатына байланысты болмаса, (1.15) функциясын координаттық және спиндік функциялардың көбейтіндісі түрінде жазуға болады. Спиндік функцияны тік жолдан тұратын матрица түрінде жазамыз.

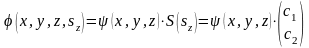. (1.16)

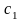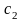Бұндағы және нормалау шарттарынан анықталатын тұрақтылар. Олардың модульдерінің квадраттары, спиннің бір өстің бойындағы проекциялары тиісінш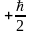е , немесе 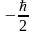болу ықтималдықтарын береді. Спиндік толқындық функция спиннің бір өстің бойындағы проекциясына сәйкес 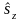және оның квадратына сәйкес 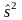операторларының меншікті функциясы болады.

; .

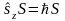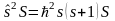Бұл жердегі 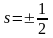мәндерін қабылдайтын спиндік кванттық сан. Бұдан бөлек, электронның ядро төңірегіндегі қозғалысына сәйкес орбиталық моменті болады. Орбиталық моменттің шамасы мен, оның бір өстегі проекциясы l орбиталық және m магниттік кванттық сандар арқылы анықталады.

; .

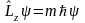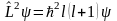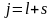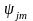Электронның толық импульс моменті, спиндік және орбиталық квант-тық сандардың қосындысы арқылы анықталады, бұл кванттық күйге сәйкес толқындық функциялар магниттік кванттық сан бойынша азғын-даған (қайталанатын) болады және олардың барлығы 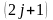санының бір мәніне, яғни энергияның бір деңгейіне сәйкес келеді. Әрбір j-дің мәніне өлшемді өрнектеу анықталады. Вигнер теоремасы бойынша олар келтірілмейтін өрнектеу тобын құрайды.

Егер спин жартылай бүтін болса, j-дің мәні де жартылай бүтін болады. Бұл жағдайда келтірілмейтін өрнектеудің айтарлықтай ерекшелігі бар. Жүйені Z өсінің төңірегінде 2π бұрышқа бұрған кезде, базистік толқын-дық функциялар былай түрленеді:

.

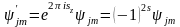Егер спин бүтін сан болса, функция өзіне түрленеді, ал жарты болса, таңба-сын кері өзгертеді. Екінші жағынан алғанда 2π бұрышқа бұру, түрлендірудің Е бірлік элементіне сәйкес келеді. Олай болса, j-дің жартылай бүтін мәні үшін екі түрлі өрнектеу матрицасы анықталады. Ол матрицалардың сипаттарының таңбалары қарама-қарсы болады. Екі түрлі келтірілмейтін өрнектеуді анықтау үшін топқа 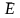жаңа түрлендіру элементін енгіземіз. Бұл симметриялы түрлендіру элементі жүйені кез келген өстің төңірегінде 2π бұрышқа бұру болсын. Бұл элементті екі рет қолдану 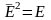бірлік элементті береді. Сондықтан n-ретті өстің төңірегіндегі бұру түрлендіруін n рет қолдану және 2n рет қолдану арқылы мына қатынастарды жазамыз:

, .

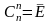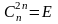Инверсия І операторы барлық бұру операторларымен коммутация жасайтындықтан, 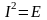. Ал айналық шағылу үшін 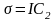болғандықтан, 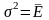, 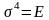болады. Сондықтан алғашқы нүктелік симметрия топтарынан, элементтерінің саны екі есе көп нүктелік симметриялы түрлен-діру тобын аламыз. Бұны қос нүктелік симметрия тобы дейді.