1.11 Зоналық құрылымды есептеудің kp-әдісі

Шала өткізгіштердің Бриллюэн зонасының барлық көлемінде энергетикалық сперктрін іс жүзінде анықтау үшін күрделі есептеулер жүргізуге тура келеді. Басты қиындық – өзімен өзі келістірілген кристалдық потенциал таңдап алуға тіреледі. Қандай-да бір жолмен энергетикалық спектрді толық анықтағанмен, оның практикалық маңызы шамалы болып қалады.

Көпшілік жағдайда шала өткізгіштің барлық зонадағы энергетикалық спектрін анықтаудың қажеті шамалы. Себебі, негізгі заряд тасымалдаушылар концентрациясы онша үлкен болмаған жағдайда олар Бриллюэн зонасының кейбір экстремалды нүктелеріне жақын күйлерде ғана орналасады. Сондықтан зоналық құрылымның осы экстремум нүктелерінің маңындағы күйлерін білу жеткілікті болады. Өткізгіштік зонаның түбіне, немесе валент-тік зонаның төбесіне жақын нүктелердегі энергетикалық спектрді есептеу үшін, біріншіден кристалдың симметриясы ескерілу керек, екіншіден, алын-ған нәтижелерді эксперименттен анықталған шамалармен салыстырып, зоналық құрылымның кейбір параметрлері анықталады.

Зонадағы экстремум нүктелерінде құраушылары бойынша есептелген дербес туындылардың барлығы нөлге тең болу керек.

. (1.111)

Бұл жердегі n – энергетикалық зонаның нөмірі.

Энергетикалық зонаның экстремумы Бриллюэн зонасының кез келген нүктесінде болуы мүмкін, бірақ ол нүктелерде, k-кеңістіктегі барлық бағыт бойынша туындылар нөлге тең болу керек. Экстремум нүктелерін топтар теориясына сүйеніп таңдап алуға болады. Кристалдың симметриясына байланысты, электронның барлық бағыттағы жылдамдықтары нөлге тең болатын экстремалды нүкте болады. Экстремалды нүктелер көбінесе зонаның центрінде болады. Кейбір симметрия сызықтарының бойында k-кеңістіктегі екі бағыт бойынша туынды нөлге тең болуы мүмкін.

экстремум нүктесінің төңірегіндегі энергия спектрін зерттеу, квант-тық механикадағы аза ауытқу теориясына негізделген, kр-әдіс деп аталған зерттеу әдісі.

Бір электрондық жуықтауда жазылған,

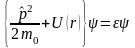, (1.112)

Шредингер теңдеуінің меншікті функциялары,

(1.113)

түрдегі Блох функциясы болады. Шредингер теңдеуіндегі – электронның импульсіне сәйкес оператор. Блох функциясын Шредингер теңдеуіне қойып, эксонентаға қысқартқан соң, периодтылығы кристалдық тор периодындай, модуляциялаушы функция үшін теңдеу аламыз.

(1.114)

Бұл теңдеуді (1.112) Шредингер теңдеуімен салыстырсақ, соңғы теңдеудегі Гамильтон операторында қосылғышы артық екенін көреміз. Бұл мүшені кристалдық потенциалға жасалған аз түзету ретінде қабылдауға болады, сондықтан оны -ауытқу деп атайды. Бұл қосылғыш ешқандай реал потенциалды білдірмейді, оның пай да болуы, Блох функциясы үшін жазылған теңдеудің орнына, орнына үшін теңдеуге көшудің нәтижесі. (1.114) теңдеуде -мүшенің болуы,

(1.115)

Гамильтон операторының, k толқындық векторды өзгерпейтін симметриялы түрлендірулерге қарағанда инвариантты болуын талап етеді. Сондықтан функциясы толқындық вектор тобының келтірілмейтін өрнектеулері бойынша түрленеді, ал (1.112) теңдеуінің шешімі Блох функциясы кристалдың нүктелік тобының келтірілмейтін өрнектеулері бойынша түрленетін еді.

(1.114) теңдеуінің шешімін қандай-да бір ортогональ функциялардың толық жүйесі бойынша жіктеу түрінде іздейміз. Егер k-ны тұрақты деп алсақ, әртүрлі n үшін жазылған периодты функциялар жиыны толық ортогональ жүйе құрайды. Тұрақты толқындық вектор үшін нүктесін таңдап алсақ, теңдеудің шешімін Вигнер-Зейтц элементар ұясына нормалан-ған ортогональ функциялар бойынша жіктеу түрінде жазамыз:

. (1.116)

Бұл функцияны өрнектеудегі функция деуге болады. (1.115) Гамилтон операторының бөлігін бөліп алсақ, (1.114) теңдеуін мына түрде жазамыз:

(1.117)

Бұл жердегі

.

(1.116) жіктеуін (1.117) теңдеуіне қойып, теңдеудің екі жағын функциясына көбейтіп, бір элементар ұяның көлемі бойынша интегралдап, энергияның меншікті мәндерін анықтауға арналғын теңдеу аламыз:

, (1.118)

Бұл жердегі нүктесінде анықталған импульс операторына сәйкес матрицалық элемент

. (1.119)

(1.118) теңдеуін алған кезде, функциялары Вигнер – Зейтц элементар ұясына нонмаланғынын ескердік, яғни

.

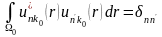(1.116) жіктеудің коэффициенттерін анықтауға арналған, (1.118) біртекті теңдеулер жүйесінің нөлден өзгеше шешімі болу үшін белгісіздер алдындағы коэффициенттерден құралған анықтауыш нөлге тең болу керек.

. (1.120)

(1.120) секулярлық теңдеуін арқылы шешіп, энергияның мүмкін болатын меншікті мәндерін анықтаймыз. Ол үшін нүктесіндегі энергияның мәні 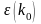, және сол нүктедегі матрицалық элемент белгілі болу керек. Бұл шамаларды тәжрибелерден анықтауға болады, сондықтан -әдіс – эмпирикалық әдіс болып табылады.