КІРІСПЕ

Қатты дене ішіндегі электронның күйі, Бриллюэн зонасындағы толқындық вектордың мүмкін болатын N мәніне сәйкес толқындық функ-циялар арқылы сипатталады. Бұл күйлердің зоналарға бөлінетінін өткен тақырыптардан білеміз. Зоналады электрондардың толтыруына байланысты қатты денелер бірнеше топқа бөлінеді.

Паули принципі бойынша, әрбір кванттық күйде спиндері қарама-қарсы екі электрон орналасатын болғандықтан, әрбір энергетикалық зонаға бар-лығы 2N электрон орналаса алады. Атомның сыртқы электрондық қабатына тиісті зонаны валенттік электрондар толық толтырған болса, ондай қатты дене электр тоғын өткізе алмайды. Валенттік зонадағы электрондар сыртқы электр өрісінің әсерінен өздерінің күйлерін өзгерте алмайды, себебі зонада бос кванттық күй жоқ.

Бір валентті элементтерден құрылғын кристалдық дене қарастырайық. Мысалы: литий, натрий, калий, рубидий, т.с.с. элементтердің сыртқы электрондық қабатында бір электроннан ғана бар. Осындай N атом кристалға біріккенде, сыртқы электрондық қабатқа сәйкес зонаға әр атом бір электроннан береді, ал зонадағы кванттық күй саны 2N, сондықтан зона жартылай толтырылады. Сонда зонада бос орындар көп болғандықтан, электрондар сыртқы электр өрісінің әсерінен кванттық күйлерін өзгерте алады, яғни кристалл ішінде қозғалысқа келеді. Бұндай кристалдық қатты дене – металл болады. Металдар жақсы өткізгіштер болып табылады.

Екі валентті элементтер, мысалы: бериллий, магний, кальций, стронций, барий кристалға біріккенде, валенттік зонаға екі электроннан береді. Сондықтан валенттік зона толық толтырылады да, қатты дене изолятор болу керек еді, бірақ жоғарыда аталған элементтерден құралған кристалдық қатты дене металдар болады. Бұл құбылысты былай түсіндіруге болады: Атомдағы валенттік электрондарға сәйкес қабаттан жоғары жатқан рұқсат етілген энергетикалық деңгейлер бос. Кристалға біріккенеде бұл деңгейлер де зонаға бірігеді, бірақ бұл зона толықтай бос. Электрондардың өзара әсерлесуі нәтижесінде, жоғарыдағы бос зонаның түбіндегі ең төменгі күйлер, валенттік зонаның төбесіндегі кванттық күйлерден төмен орналасады. Басқаша айтқанда, валенттік зона мен, одан жоғары жатқан бос зона біршама айқасады. Бұл кезде валенттік зона төбесіндегі электрондардың біразы, одан төмен жатқан өткізгіштік зонаның түбіне көшеді, себебі ондай орналасу – энергетикалық жағынан ұтымды. Электрон әрқашан төменгі энергетикалық күйлерге орналасуға тырысады. Нәтижесінде валенттік зонаның төбесінде бос кемтіктер, ал өткізгіштік зона түбінде бос электрондар пайда болады. Ол екеуі де заряд тасымалдауға қатыса алады. Бұндай кристалдық қатты денелерді – шала металдар деп атайды.

Валенттік зона толық толтырылған, және жоғары жатқан өткізгіштік зонамен айқаспайтын болсын. Валенттік зонаның төбесі мен өткізгіштік зонаның түбін E_g – рұқсат етілмеген зона бөліп жатсын. Бұл жағдайда қатты денені екі топқа бөлуге болады.

1) 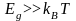, рұқсат етілмеген зонаның ені, электронның жылулық қозғалыс энергиясынан әлдеқайда үлкен болсын. Бұл кезде валенттік зонадағы электрондардың жылулық қозғалысының энергиясы оларды өткізгіштік зонаға көшіруге жетпейді, сондықтан өткізгіштік зона толықтай бос, ал валенттік зона толық толтырыған күйде қалады. Бұндай кристалдық қатты дене идеал диэлектрик болады.

2) Керісінше, 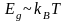болсын. Бұл кезде валенттік зонаның төбесіндегі біраз электрондар, жылулық энергиясы есебінен, өткізгіштік зонаның түбіндегі бос орындарға көшеді, және валенттік зона төбесінде оң зарядталған кемтіктер пайда болады. Егер бос электрондар мен кемтіктердің концентрациясы бірдей болса, ондай кристалдық денелерді – меншікті шала өткізгіштер деп атайды. Шала өткізгіштегі бос электрондар мен кемтіктер заряд тасымалдауға бірдей қатысады. Меншікті шала өткізгіштердің электр өткізгіштігі температураға байланысты өсетіндігі түсінікті.

Шала өткізгіштердің келесі тобын – қоспалы шала өткізгіштер деп атайды. Валенттік зона мен өткізгіштік зона арасында, рұқсат етілмеген зона аумағында, қоспа атомдар себебінен болатын энергетикалық деңгейлер пайда болуы мүмкін. Бұларды қоспа деңгейлері деп атайды. Қоспа деңгейлері донорлық және акцепторлық болып екіге бөлінеді.

Элементтер кестесіндегі төртінші топтың элементтарі алмаз типті кристалға бірігеді. Алмаз типті кристалдық тордағы әр атомның ең жақын төрт көршісі болады және берілген атомдағы төрт валенттік электрон сол көршілермен валенттік байланыс құрайды. Алмаз типті тордың бір элементар ұясына екі атомнан келеді. Олардағы электрондардың саны жұп болғандықтан валенттік зонаны толық толтырады. Сондықтан төртінші топ элементтерінен құрылған кристалл не диэлектрик, немесе шала өткізгіш болады. Көміртегі атомдарынан құралатын алмаз – диэлектрик, ал кремний, германий сияқты кристалдар – шала өткізгіштер болады. Осы шала өткізгіштер кристалында бөгде атомдардан қоспа қосылса, олар қоспалы шала өткізгіштерге айналады. Мысалы, алмаз типті кристалдық тордағы бір атомды бес валентті мышяк атомын алмастырсақ, ондағы бес электронның төртеуі көршілермен валенттік байланысқа түсіп, бір электрон бос қалады. Бос қалған электронға сәйкес энергетикалық деңгей өткізгіштік зонасының түбіне жақын орналасады. Ол деңгейді – донорлық деп атайды. Егер донорлық деңгей мен өткізгіштік деңгей арасы жақын болса, донорлық электрон өткізгіштік зонаға оңай өтіп, бос электорнға айналады. Ондай қоспалы шала өткізгішті электрондық, немесе n-типті (negative) шала өткізгіш деп атайды.

Егер аталған кристалдарға үш валентті, мысалы индий атомдарынан қоспа қосылса, онда акцепторлық шала өткізгіш алынады. Валенттік байланыс жасауға бір электрон жетпей қалғандықтан, оның бос орыны кемтікке айналады. Кемтікке сәйкес акцепторлық деңгей валенттік зонаның төбесіне жақын орналасады. Сондықтан валенттік зона төбесіндегі электрондар, жылулық энергия есебінен акцепторлық деңгейге оңай көшеді. Нәтижесінде валенттік зона төбесінде оң зарядталған кемтіктер пайда болады және олар заряд тасымалдауға қатысады. Акцепторлы қоспалар қосылған шала өткізгішті р-типті (pozitive) шала өткізгіш деп атайды.

І тарау. Энергетикалық зоналар құрылымын есептеу әдістері

1.1 Мәселенің қойылуын талдау

Қатты денелердің зоналық құрылымы туралы мәліметтерді білу, яғни әрбір энергетикалық зонадағы электрондар энергиясының толқындық векторға тәуелділігін анықтаудың практикалық маңызы зор. Әртүрлі зоналардың өзара орналасуы, олардағы экстремум нүктелері берілген қатты дененің электрлік қасиеттерін толықтай анықтайды.

Кристалл ішіндегі электронның энергетикалық спектрі, бір элек-трондық жуықтаудағы Шредингер теңдеуін шешу арқылы анықталады.

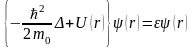. ( 1.1)

Бұл жердегі 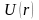− кристалдық периодты потенциал.

(1.1) теңдеуінің меншікті функциялары мен меншікті мәндерін анықтау есебін екі кезеңге бөлуге болады. Біріншіден, берілген кристалдық торды сипаттайтын кристалдық потенциалың түрін анықтап алу керек. Бірақ өкінішке орай, оны дәл анықтау мүмін емес. Екінші тарауда көрсетілгендей, Хартри−Фок әдісімен, өзімен-өзі келістірілген потенциал таңдап алуға болады. Бірақ өте күрделі есептеулер жасалау керектігінен бұл әдістің дәлдігі төмендейді. Алғашқы жуықтау әдісін Слэтер ұсынған [15]. Ол алмасу арқылы әсерлесу потенциалын, кристалдағы электрондардың орташа тығыздығының кубтық түбірімен алмастыруды ұсынды. Бірақ бұл әдіс қойылған проблеманы шешпейді. Сондықтан потенциалды жуықтап табыл-ған шамалардың эксперимент нәтижелерімен қаншалықты жақындығын тексере отырып таңдап алу керек.

Есептің екінші кезеңі, таңдап алынғын потенциал үшін (1.1) теңдеуін шешу әдісі біршама жақсы зеттелген. Металдар мен шала өткізгіштердегі электрондардың энергетикалық спектрін есептеу үшін арнайы бағдарламалар жасалған және оларды эксперимент нәтижелерімен жақсы қабысатындай етіп таңдап алуға болады [16].

Бұл әдістердің барлығы, (1.1) теңдеуінің шешімін белгілі шекаралық шарттарды қанағаттандыратын функциялардың толық жүйесі бойынша қатар түрінде іздеуге негізделген.

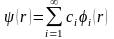. (1.2)

Өзара ортогональ функциялардың толық жүйесін алсақ, (1.2) қосындысы шексіз көп мүшелерден тұрар еді. Іс жүзінде жіктеудің шексіз көп коэффициенттері с_і үшін теңдеуді шешу мүмкін емес. Сондықтан шектеулі 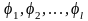функциялар жүйесін алып, теңдеудің шешімін олардың сызықты комбинациясы түрінде іздейді.

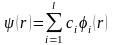. (1.2а)

Кристалл ішіндегі электронның толқындық функциясы, (1.41) Блох функциясы түрінде болу керек.

.

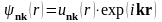Бұл жердегі k – бірінші Бриллюэн зонасына келтірілген толқындық вектор және оған сәйкес толқын ұзындығы 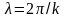атомдар ара қашықтығынан үлкен болу керек. Блох функциясы, тордың периодтылығымен бірдей, 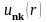функциясымен модуляцияланған, жазық толқын 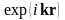түрінде болады. Блох функциясы атомдар аралығында жазық толқын, ал атомдарға жақын жерлерде тез өзгеретін атомдық функциялар түрінде болу керек. Ол үшін функциясы атомның маңында тез өзгеруі керек. Блох функциясының бұл қасиетіне қарап, (1.2) жіктеуіндегі ортогональ функциялардың толық жүйесі үшін жазық толқындар, немесе сфералық толқындар алу керектігі көрінеді.

Блох функциясы 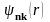периодты болғандықтан, (1.1) теңдеуінің шешімін бір элементар ұя ішінде анықтау жеткілікті. Кристалдық тор ішіндегі бір атомның төңірегіндегі Вигнер – Зейтц элементар ұясының шекарасы, көрші атомдарды қосатын түзулердің ортасы арқылы өтетін жазықтықтардан құралған, көпжақты тұйық бет болады. Осындай ұяларды тығыз орналастырсақ, олар барлық кеңістікті саңылау қалдырмай толтырады. Шредингер теңдеуінің шешімі ұялардың шекараларында мына шекаралық шарттарды қанағаттандыру керек:

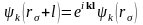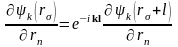, . (1.3)

Бұл жердегі 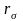және ( 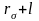) нүктелері, элементар ұяның қарама қарсы жақтарындағы трансляция векторымен ажыратылған нүктелер, ал дербес туындылар – сол нүктелердегі сыртқы нормаль бағыты бойынша алынған.

Бірінші шекаралық шарттың орындалуы функцияның периодтылығымен байланысты. Кристалл ішіндегі, бір-бірінен трансляция векторына ажыра-тылған эквивалентті нүктелердегі толқындық функциялардың бір бірінен айырмашылығы тек 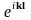фазалық көбейткіште болу керек. Себебі, стационар жағдайда бұл нүктелерде электронның болу ықтималдықтары бірдей. Екінші шекаралық шарттың орындалуы, толқындық функциялардың шекарада үздіксіз болуымен қатар, олардың бір-бірімен жылтыр қабысуын қамтамасыз етеді.

Есептің осылай қойылуын – ұялар әдісі деп атайды. Ұяның центріне жақын нүктелердегі толқындық функцияларды сфералық симметриялы деуге болады. Сондықтан Шредингер теңдеуінің шешімін, радиалдық функция-лардың қосындысы түрінде іздеуге болады. Жіктеудің коэффициенттерін, (1.3) шекаралдық шарттары элементар ұя шекарасындағы кейбір нүктелерде орындалатындай етіп таңдап алады. Кристалдағы электронның толқындық функциялары мен энергияларын кейбір қатты денелер үшін Слэтер ұялар әдісімен анықтаған [15].

Ұялар әдісінің айтарлықтай кемшілігі бар. Вигнер – Зейтц элементар ұясының формасы күрделі болғандықтан, оның шекарасындағы барлық нүктелер үшін шекаралық шартты қолдана алмаймыз. Сондықтан элементар ұяның шекаралық беттерінің центрінде ғана (1.3) шартының орындалуын талап етуге болады. Бұл (1.2а) жіктеуіндегі сфералық симметриялы радиал функцияның санын азайтады, нәтижесінде алынған шешім реал жағдайдан алшақ болып шығады. Ал шекаралық шарт орындалатын нүктелер санын көбейту есептеулерді тым қиындатып жібереді.

Шекаралық шарттарды қолдануды жеңілдету үшін, Вигнер – Зейтц көпжақты элементар ұясын сферамен алмастырады. Сферамен шектелген ұяның көлемі реал элементар ұя көлеміне тең болатындай етіп алынады.

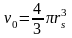. (1.4)

Бұл жердегі 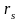− Вигнер – Зейтц сферасының радиусы.

(1.3) шекаралық шарттары бойынша, сфераның бетіндегі барлық нүктелерде толқындық функция мен оның бірінші туындылары үздіксіз болуы жеткілікті. Бұл әдіс Бриллюэн зонасының центріндегі s-типті зоналар үшін жақсы нәтиже бергенімен, басқа нүктелер үшін жарамайды.

Келесі әдіс – вариациялық деп аталады. Вариациялық әдіс бойынша, (1.1) теңдеуін шешуді, қандай-да бір 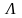функционалдың минимумын анықтаумен алмастырылады.

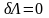. (1.5)

(1.2а) жіктеуін (1.1) теңдеуіне қойып, екі жағын 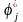комплекс түйіндес функцияға көбейтіп, кристалдың барлық көлемі бойынша интегралдаймыз. Сонда, жіктеудің коэффициенттерін анықтауға арналған алгебралық теңдеулер жүйесіне келеміз:

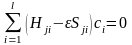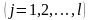, . (1.6)

Бұндағы,

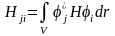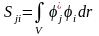, . (1.7)

(1.2а) жіктеуіндегі функциялар өзара ортогональ болуы шарт емес, сондықтан .

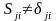(1.6) біртекті теңдеулер жүйесінің нөлден өзгеше шешімі болу үшін коэффициенттерден құрылған детерминант нөлге тең болу керек.

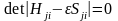. (1.8)

Бұл секулярлық теңдеу, белгісіз ε-ге қарағанда l дәрежелі теңдеу болып табылады. Теңдеудің l түбірінің ең кішісі зонадағы ең төменгі күйдің энергиясын берсе, қалған түбірлері жоғарғы күйлерге сәйкес келеді.

(1.2а) жіктеуіндегі 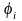базистік функциялар орнына, алғаш тексеріп көру үшін белгілі функциялар жиыны алынады. (1.2а) функциясы үшін

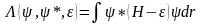
функционал құрылады. Бұл формулаға (4.2а) жіктеуін қоямыз.

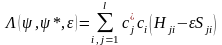. (1.9)

Ол функционал үшін вариациясы нөлге тең болсын. Сонда,

,

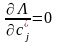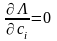
шарттары орындалу керек. (1.9) функционалының с_і бойынша дербес туындыларын нөлге теңестіру арқылы мына теңдеулер жүйесін аламыз:

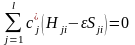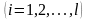, . (1.10)

Соңғы теңдеулер жүйесі, (1.6) теңдеулер жүйесінің комплекс түйіндесі екенін көреміз. Себебі бұл жердегі операторлар эрмиттік екені белгілі. Бұл жуықтаудың дәлдігі, алғаш тексеріп қөру үшін алынған базистік функция-ларына байланысты.

Сыртқы электрондық деңгейлерге сәйкес зоналар үшін базистік функциялар ретінде жазық толқындар алу жақсы нәтиже береді, себебі ол кезде бос электрондық жуықтау алынады. Ал төменгі деңгейлерге сәйкес зоналар үшін базистік функцияларды, тез өзгеретін атомдық функциялар түрінде алу керек. Базистік функцияларды таңдап алуға байланысты энергетикалық зоналарды есептеу әдістері де әртүрлі болады:

1. Атом орбиталарының сызықты комбинациясы әдісі;

2. Тіркестірілген жазық толқындар әдісі;

3. Грин функциясы әдісі;

4. Ортогоналдырылған жазық толқындар әдісі;

5. Псевдопотенциал әдісі;

6. Түрлі интерполяцыиялық әдістер (kp-әдісі, комбинациялық әдістер).