3. Обробка результатів, оформлення звіту

ТА ВИСНОВКИ ПО РОБОТІ

Звіт повинен містити:

- назву лабораторної роботи та її мету;

- схематичний вигляд передньої панелі осцилографа;

- заповнені таблиці вимірювань;

- результати розрахунків;

- висновки по кожному пункту досліджень.

4 Контрольні запитання

4.1 Пояснити принцип роботи осцилографа.

4.2 Пояснити призначення функціональних блоків структурної схеми осцилографа.

4.3 Пояснити призначення ручок управління осцилографом.

4.4 Розповісти про види розгорток електронного променя.

4.5 Коли застосовується очікувальна розгортка?

4.6 Які значення напруги вимірюються осцилографом?

4.7 Які значення напруги вимірюються вольтметром і комбінованим приладом?

4.8 Які параметри електричних сигналів можна виміряти осцилографом?

4.9 Які параметри електричних кіл та сигналів можна виміряти комбінованим приладом?

4.10 Пояснити різницю у вимірюванні осцилографом постійної і змінної напруги.

Лабораторна робота №2 “Дослідження трифазних кіл електроживлення” Мета роботи – виконати дослідження симетричних та несиметричних трифазних кіл при з’єднанні навантаження зіркою та трикутником.

1 Теоретичні відомості

Під трифазною симетричною системою ерс (електрорушійних сил) розуміють сукупність трьох синусоїдних ерс однакових частоти та фази, які зміщені між собою по фазі на 120⁰. Для того, щоб відрізнити три ерс у системі, одну з них позначають е_А (фаза А), ту, яка відстає від неї на 120⁰ – е_В (фаза В) і ту, яка випереджає її – е_С (фаза С). Відповідно до цього миттєві значення фазних ерс виражаються такими формулами (якщо за t = 0 прийняти момент часу, коли напруга фази А проходить через нуль і стає додатною):

(2.1)

В комплексному виді (при суміщенні дійсної осі з напругою фази А) фазні напруги записуються:

(2.2)

На рисунку 2.1 наведений графік миттєвих значень ерс всіх трьох фаз.

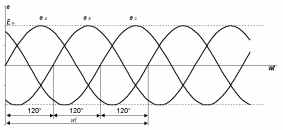
Рисунок 2.1 - Графік миттєвих значень е_А, е_В, е_С

Напруги на обмотках трифазного джерела зручно показати у вигляді векторної діаграми, рисунок 2.2.

Трифазне коло складається з трифазної системи ерс (генератор), трифазного навантаження та з’єднувальних проводів. На схемах трифазний генератор наводять у вигляді трьох обмоток, які найчастіше з’єднують зіркою. Прийнято вважати початком кожної фази ту її точку, в якій позитивно спрямований струм надходить з обмотки генератора у зовнішнє коло, і кінцем фази – ту точку, в якій позитивно спрямований струм надходить із зовнішнього кола в обмотку генератора. Початки фаз позначають буквами А, В, С, а кінець – буквою О.

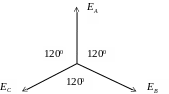
Рисунок 2.2 - Векторна діаграма напруг трифазного джерела

Якщо навантаження фаз мають однакову величину і характер, то струми в них І_А, І_В, І_С будуть однаковими за величиною і зміщені на однакові кути φ відносно відповідних ерс. Між собою ці струми будуть мати також зсуви 120⁰ (як і ерс), отже, як легко побачити з векторної діаграми, рисунок 2.2, струми у фазах будуть об’єднані таким співвідношенням:

(2.3)

Таке навантаження називається симетричним.

Рисунок 2.3 - Схема з’єднання навантаження зіркою

Обмотки фаз генератора, три однофазних генератори або три навантаження можна з’єднати за схемою зірки або трикутника.

На рисунку 2.3 наведена схема з’єднання навантаження зіркою. Спільна точка, в якій об’єднані кінці фаз генератора (або приймача - навантаження), називається його нульовою точкою або нейтраллю, а провід, що з’єднує нульові точки О і О₁ – нульовим або нейтральним проводом. Струм у нейтральному проводі, як видно із схеми, є сумою фазних струмів:

(2.4)

Напруги між початками фаз генератора або приймача і його нейтраллю, які позначаються U_A, U_B, U_C, називаються фазними напругами. Напруги між початками фаз відповідно А і В, В і С, С і А, які позначаються U_AB, U_BC i U_CA, називаються лінійними напругами. Враховуючи, що точка О є точкою нульового потенціалу, а точкам А, В і С відповідають фазні напруги U_A, U_B і U_C (потенціали цих точок дорівнюють фазним напругам), то лінійні напруги можна записати у такому вигляді:

(2.5)

Наведену операцію віднімання зручно продемонструвати на векторній діаграмі шляхом додавання векторів і , і , і . Це показано на рисунку 2.4. З діаграми видно, що величина і напрямок векторів лінійних напруг можуть бути отримані простішим шляхом, якщо з’єднати прямою лінією кінці векторів відповідних фазних напруг, причому вектор лінійної напруги спрямований від кінця того, що віднімається, до кінця того, від якого віднімають. Три вектори лінійних напруг однакові за величиною і повернуті між собою, як і фазні напруги, на кут 120⁰. При цьому зірка лінійних напруг зміщена відносно зірки фазних напруг на кут 30⁰ вперед. Якщо розглянути будь-який рівнобедрений трикутник (наприклад ΔОАВ) з кутом при вершині 120⁰, то можна отримати важливе співвідношення між лінійною і фазною напругами для трифазного кола при з’єднанні навантаження зіркою:

(2.6)

-U_B

А

U_AB

U_CA U_A U_AB U_BC

O

U_C U_B -U_C

C U_BC B

-U_A U_CA

Рисунок 2.4 - Векторна діаграма фазних та лінійних напруг

Зі схеми, рисунок 2.3, видно, що для з’єднання навантаження зіркою лінійний струм дорівнює фазному:

(2.7)

Розглянемо тепер з’єднання навантаження трикутником. Схема такого з’єднання наведена на рисунку 2.5.

Рисунок 2.5 - Схема з’єднання навантаження трикутником

При такому з’єднанні не розрізняють фазні і лінійні напруги, оскільки напруга між початком і кінцем кожної фази приймача (навантаження) виявляється в той же час і лінійною напругою. Але з’являється різниця між фазними струмами навантаження і та лінійними струмами і Згідно з законом Кірхгофа для наведеної схеми можна записати:

(2.8)

Із співвідношень (2.8) витікає, що сума лінійних струмів дорівнює нулю:

(2.9)

Векторна діаграма зображена на рисунку 2.6. На цій діаграмі показане векторне віднімання фазних струмів відповідно до співвідношень (2.8) (аналогічно з’єднанню навантаження зіркою). Векторна діаграма відповідає випадку симетричного навантаження, коли фазні струми і рівні за величиною і зміщені на однакові кути відносно відповідних фазних (лінійних) напруг U_AB, U_BC i U_CA. Лінійні струми і також виявляються рівними між собою і симетрично розташованими, причому зірка лінійних струмів зміщена відносно зірки фазних струмів на 30⁰ назад.

U_AB

-I_CA

I_AB I_A

I_C

-I_BC

I_CA

I_BC

U_CA U_BC

-I_AB

I_B

Рисунок 2.6 - Векторна діаграма фазних та лінійних струмів

Вектор кожного з лінійних струмів, рисунок 2.6, є основою рівнобедреного трикутника з кутом 120⁰ при вершині, тому між значеннями лінійного і фазного струмів при симетричному навантаженні та з’єднанні його трикутником має місце таке ж співвідношення, як і між лінійною та фазною напругами при з’єднанні навантаження зіркою, отже:

(2.10)

Як вже зазначалось, для з’єднання навантаження трикутником справедливе також таке співвідношення:

(2.11)

Потужність трифазної системи дорівнює сумі потужностей окремих фаз:

активна

(2.12)

реактивна

(2.13)

повна

(2.14)

Для симетричного навантаження маємо:

(2.15)

Якщо брати до уваги співвідношення між лінійними і фазними напругами і струмами (2.6, 2.7, 2.10, 2.11), а також співвідношення (2.15), то для симетричної трифазної системи незалежно від схеми з’єднання (зірка чи трикутник) потужності можна визначити так:

активна

(2.16)

реактивна

(2.17)

повна

(2.18)

Коефіцієнт потужності для трифазної системи визначається як відношення активної потужності до повної або через відповідні опори:

(2.19)

(2.20)

Очевидно, активна і реактивна потужності в будь-якій фазі можуть бути визначені з використанням відомого співвідношення (якщо відомі відповідні величини фазного струму та активного чи реактивного опорів):

(2.21)