Пример 1. Построение линейной одномерной регрессионной модели.

Зависимость предельной нагрузки на болт от его твердости приведена в виде таблицы 1 экспериментальных данных

Таблица 1

Исходные данные к примеру 1

Y = yi, усл. ед.	10,10	10,30	10,45	10,90	11,20	11,35	11,90	12,45	12,58
X = xi, усл. ед.	50,0	50,2	52,8	53,5	54,0	56,8	58,8	59,5	60,5

Продолжение таблицы 1

Y = yi, усл. ед.	12,96	13,44	13,60	13,95	14,50	14,98	15,48	15,96	16,50
X = xi, усл. ед.	64,8	65,4	68,4	69,2	70,5	74,5	76,8	78,5	80,0

Необходимо:

1) построить математическую модель предельной нагрузки на болт от его твердости , приняв в качестве нулевой гипотезы линейную зависимость;

2) проверить правильность выбранной гипотезы, определив коэффициент корреляции;

3) найти доверительный интервал для полученной функции регрессии с заданной надежностью .

Построение математической модели

Построив корреляционное поле экспериментальных данных (рис. 1), выдвигаем гипотезу о линейной зависимости между и . Тогда математическую модель будем строить в виде

.

Д ля определения коэффициентов и воспользуемся методом наименьших квадратов. Составим вспомогательную таблицу 2.

Таблица 2

Расчетные данные

№ з/п	хі	уі		хі уі
1	50	10,1	2500	505	102,01
2	50,2	10,3	2520,04	517,06	106,09
3	52,8	10,45	2787,84	551,76	109,2025
4	53,5	10,9	2862,25	583,15	118,81
5	54	11,2	2916	604,8	125,44
6	56,8	11,35	3226,24	644,68	128,8225
7	58,8	11,9	3457,44	699,72	141,61
8	59,5	12,45	3540,25	740,775	155,0025
9	60,5	12,58	3660,25	761,09	158,2564
10	64,8	12,96	4199,04	839,808	167,9616
11	65,4	13,44	4277,16	878,976	180,6336
12	68,4	13,6	4678,56	930,24	184,96
13	69,2	13,95	4788,64	965,34	194,6025
14	70,5	14,5	4970,25	1022,25	210,25
15	74,5	14,98	5550,25	1116,01	224,4004
16	76,8	15,48	5898,24	1188,864	239,6304
17	78,5	15,96	6162,25	1252,86	254,7216
18	80	16,5	6400	1320	272,25
Σ	1144,2	232,6	74394,7	15122,38	3074,654

Вычислим коэффициенты линейной регрессии по формулам

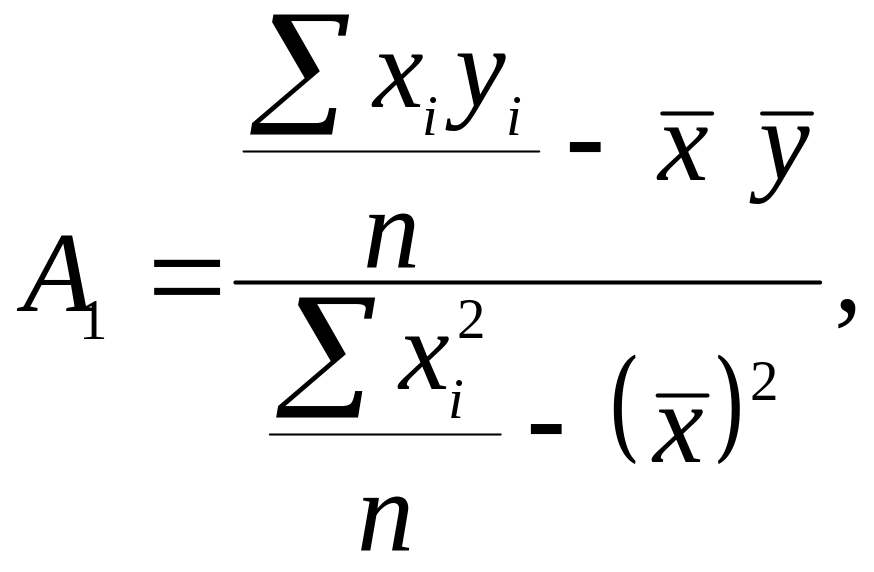
Т.к. n = 18, то

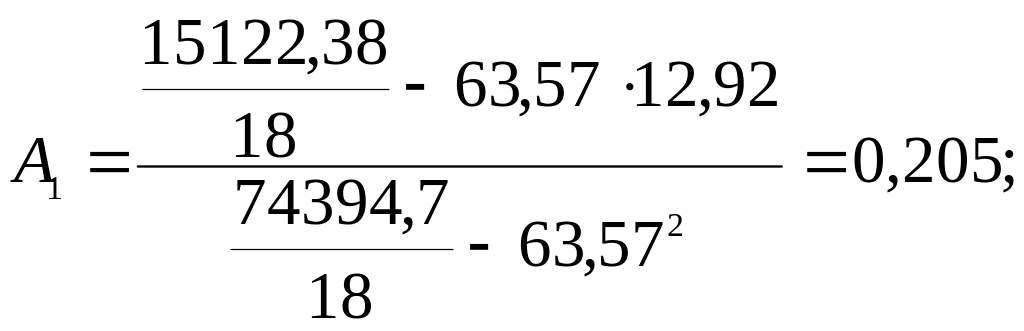
Следовательно, математическую модель зависимости предельной нагрузки на болт от его твердости можно записать в виде

Для проверки правильности выдвинутой гипотезы о линейности модели вычислим коэффициент корреляции по формуле

Для вычисления необходимо найти

;

;

Тогда

Как видим, коэффициент корреляции близкий по своему значению к единице, что свидетельствует о том, что зависимость между Х и Y практически линейная.

Для проверки адекватности полученной математической модели построим доверительный интервал для парной линейной функции регрессии с заданной надежностью .

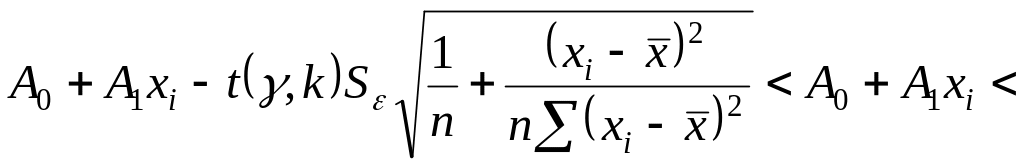
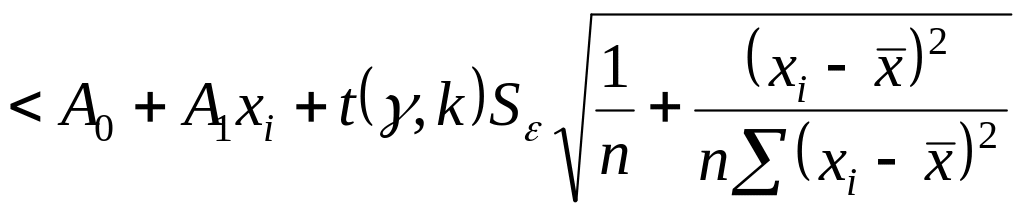
Для построения доверительного интервала функции регрессии необходимо вычислить дисперсию для :

для значений . Здесь является точечной несмещенной статистич­еской оценкой для — среднеквадратического отклонения случайного фактора

Промежуточные вычисления поместим в таблицу 3.

Таблица 3