Миттєва швидкість прямолінійного руху матеріальної точки.

0 М₀ М₁

S=0 S₀= f(t₀ ) S₁= f(t₁ ) S

t=0 t₀ t₁

ЗАДАЧА1. Нехай матеріальна точка М рухається прямолінійно по закону s=f (t). В момент часу t₀ вона зайняла положення М₀ і пройшла шлях s₀ =f (t₀). Знайдемо швидкість точки в момент часу t₀.

Припустимо, що за довільно вибраний проміжок часу ∆t, починаючи з моменту t₀ , точка перемістилась на відстань ∆s і зайняла положення М₁ .

Тоді t₁ = t₀ + ∆t, s₁ = f (t₁) = s₀ + ∆ s.

За проміжок часу ∆t матеріальна точка проходить шлях

∆x = f (t₁) - f (t₀) = f (t₀ + ∆t) - f (t₀).

Середня швидкість V_сер. руху на проміжку М₀М₁ дорівнює:

V_сер. =

Якщо проміжок ∆t буде зменшуватися, то ця величина буде більш точніша.

Таким чином, можна вважати, якщо ∆t наближається до нуля, то середня швидкість V_сер. буде наближатися до швидкості в момент часу t₀ .

О_1. Миттєвою швидкістю точки, яка рухається прямолінійно, в момент часу t₀ називається границя середньої швидкості при умові, що t наближається до нуля.

V_мит. =

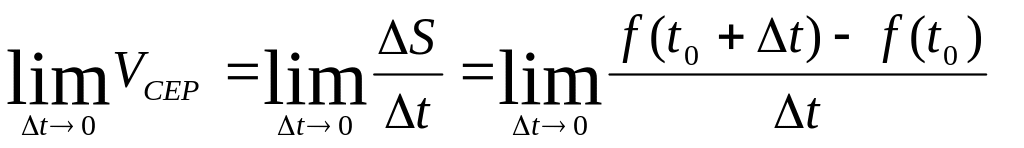
Числа ∆t, ∆s називаються відповідно приростом часу, приростом шляху.

Отже, миттєвою швидкістю точки, яка рухається прямолінійно, є границя відношення приросту шляху ∆s до відповідного приросту часу ∆t, коли приріст часу наближається до нуля.

Дотична до кривої

Розглянемо функцію y = f (x) і її графік – криву лінію.

АМ – січна. Зафіксуємо точку А. Нехай точка М, рухаючись по кривій, наближається до точки А.При цьому січна АМ буде повертатися навколо точки А і в граничному положенні при наближенні точки М до точки А січна займе положення прямої АТ. Пряму АТ називають дотичною до даної кривої в точці А.

О₂ . Дотичною АТ до графіка функції y = f (x) в точці А називається граничне положення січної АМ, коли точка М, рухаючись по кривій, наближається до точки А.

ЗАДАЧА 2. Провести дотичну до графіка функції y = f(x)

в точці А( x₀ ;y₀ ).

Положення прямої y= kx+b визначається кутовим коефіцієнтом прямої k = tg a, де a – кут між прямою і додатнім напрямом осі OX. Провести дотичну до графіка означає знайти число k.

Нехай в точці А( x₀ ;y₀ ) кривої y = f (x) існує дотична. Визначимо кутовий коефіцієнт дотичної.

Для цього:

1. Надамо аргументу x₀ приросту ∆x, одержимо нове значення аргументу .

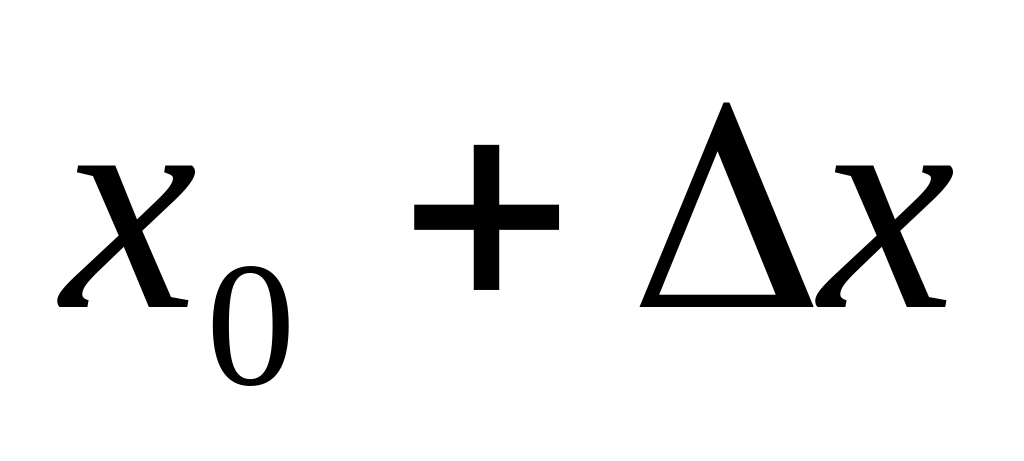2. Знайдемо відповідний приріст функції:

.

3. Знайдемо відношення: .

Із трикутника АМК маємо: tg МАК.

Так як МАК= φ – куту нахилу січної АМ з додатним напрямом осі ОX, то tg φ.

4. Якщо ∆x → 0, то ∆y → 0 і точка М буде переміщуватися по кривій, наближаючись до точки А.

Граничним положенням січної АМ при ∆x → 0 буде дотична АТ, яка утворює з додатним напрямом осі ОX деякий кут, величину якого позначимо через ά.

Отже, – кутовий

коефіцієнт дотичної.