Тема 2.2. Пределы

2.2.1.Определения.

Бесконечно малые величины – это очень важный класс переменных величин, играющий первостепен­ную роль в высшей математике. Переменная величина называется бесконечно малой в некотором процессе, если она в этом процессе безгранично приближается (стремится) к нулю. Например, при рассмотрении последовательности 1, 1/2, 1/3, ... общий ее член а_п= 1/п в процессе увеличения номера п =1, 2, 3, ... является бесконечно малой дискретной величиной. Это выражается такими словами: для любого заданного постоянного  > 0 в ходе развития процесса должен найтись момент (т.е. такой номер N), начиная с которого (т.е. при п > N) всегда будет |а_п| < . При этом нет надобности всегда такой момент фактически точно указывать: доста­точно иметь уверенность, что он когда-либо наступит. Таким образом, бесконечно малая величина в начале своего изменения может быть вовсе не малой: существенно лишь, что она в ходе развития процесса становится как угодно малой (конечно, подразумевается, по абсолют­ной величине).

Переменная величина х назы­вается бесконечно большой в некотором процессе, если она в этом процессе безгранично возрастает по абсолютной величине; тогда пишут |x| . Бесконечно большая величина может быть положительной (х , иногда пишут x +), отрицательной (х –), но может также и менять знак: например, величина x_п=(–2)^п при воз­растании номера n принимает значения –2, 4, –8, 16, .... т. е. является бесконечно большой.

Отметим некоторые простые свойства бесконечно малых и бесконечно больших.

• Вели­чина, обратная бесконечно большой, является бесконечно малой, а величина, обратная бесконечно малой, является бесконечно большой.

• Сумма или разность двух бесконечно малых есть также величина бесконечно малая.

• Сумма бесконечно большой величины и величины ограниченной является величиной бесконечно большой.

• Сумма двух бесконечно больших одинакового знака есть также бесконечно большая. В отличие от этого сумма двух бесконечно больших противоположного знака может и не быть бес­конечно большой, бесконечности могут «скомпенсироваться».

• Произведение двух бесконечно малых (больших) есть величина бесконечно малая (большая). Более того, произведение бесконечно малой на величину ограниченную есть величина бесконечно малая, соответственно, произведение бесконечно большой на величину, большую по абсолютному значению некоторой положительной постоян­ной, есть величина бесконечно большая.

• В то же время частное от деления двух бесконечно больших, подобно частному от деления двух бесконечно малых, есть неопределенность. Это записывается так

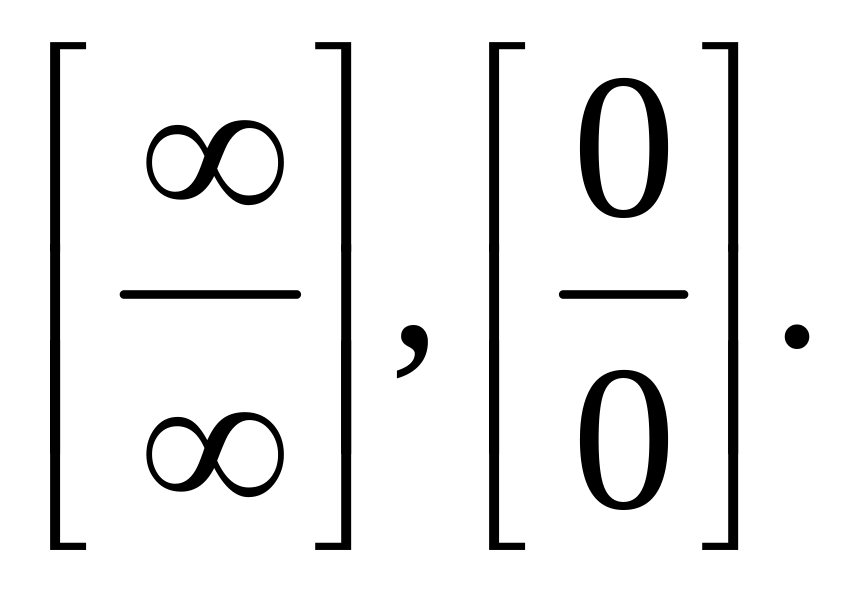
Примеры раскрытия подобных неопределенностей приведены в 2.2.3.

Говорят, что переменная величина х в некотором процессе стремится к конечному пределу а, если величина а постоян­ная и х в этом процессе безгранично приближается к а. Тогда пишут

ха или lim x=a

(lim – от латинского «limes», что значит «предел»).

Таким образом, конечным пределом переменной величины, если он имеется, служит величина постоянная.

Согласно данному определению бесконечно малые величины – это величины, стремящиеся к нулю, т.е. имеющие пределом нуль. Бес­конечно же большие величины конечного предела не имеют.

Сказать «х безгранично приближается к а» – это все равно, что сказать «разность между х и а безгранично приближается к нулю», т.е. х–а есть величина бесконечно малая.

Рассмотрим функцию . Выбирая достаточно близкое к 3,5 можно добиться, чтобы значение у сколь угодно мало отличалось от 8,25 или говорят, что стремится к 8,25 при стремлении к 3,5.

Число А называют пределом функции при ,если для любого сколь угодно малого найдется , что при . Это пишется так

Причем а может быть как (постоянная), так и 0 (бесконечно малая) или (бесконечно большая). Аналогично А может быть ,0, .

Если х < а и ха, то употребляют запись ха-0 (х стремится к а слева); если х > а и ха – запись ха+0 (х стремится к а справа). Числа f(a-0)= и f(a+0)= называются соответственно левым и правым пределом функции f(х) в точке а.