2.5.2. Частные производные, дифференциал.

Ограничимся случаем функций двух переменных, все дальнейшее справедливо и для п > 2.

Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.

Частные производные функции z=f(x,y) в точке обозначаются так:

(производная по х),

(производная по у).

Для нахождения частной производной можно использовать правила дифференцирования функций одной переменной, считая константой у.

Аналогично, для нахождения частной производной константой следует считать х.

Пример 2.5.1. Найти частные производные функций:

а) z= x/y. Считая у = const, находим Считая х = const, находим

б) z= x^y. вычисляется как производная степенной функции (у=const).

вычисляется как производная показательной функции (х=const).

Полный дифференциал.

При одновременном изменении величин х и у функция z=f(x,y) изменится на величину

z=f(x+x, y+y) – f(x,y) (2.5.1)

Величина z, заданная формулой (2.5.1), называется полным приращением функции z в точке (x у). Так же, как и в случае функции одной переменной возникает задача о приближенной за­мене приращения z. Роль ли­нейного приближения выполняет полный дифференциал фун­кции, который определяется как сумма произведений частных про­изводных функции на приращения независимых переменных. Так, в случае функции от двух переменных, полный дифференциал оп­ределяется равенством

dz = x+ y. (2.5.2)

В формуле (2.5.2) точка (х, у) явно не указана, однако, следует помнить, что в различных точках дифференциал будет раз­личным.

Пример 2.5.2. Найти полный дифференциал функции z= x/y в точках:

а)(0;2), б)(1;1).

а) dz = (1/у)x+(–х/у²)y=(1/2)x. б) dz = x – y.

2.5.3. Предельная полезность и предельная норма замещения

Основным понятием теории потребления является функция полезности U(x,у). Эта функция выражает меру полезности на­бора (х,у), где х – количество товара X, а у – количество товара Y. Чувствительность набора (х,у) к незначительному изменению х при фиксированном у называется предельной полезностью х и опре­деляется как частная производная U'_х. Аналогично предельная полезность у определяется как U'_у. Чаще всего линии уровня функции полезности (их еще называют кривыми безразличия) являются графиками убывающих функций. Поэтому мы будем считать, что для точек А(х₀, у₀) и В(х₀ + х, у₀ + у), расположенных на одной линии уровня приращения, х>0, а у < 0. (рис. 2.5.1).

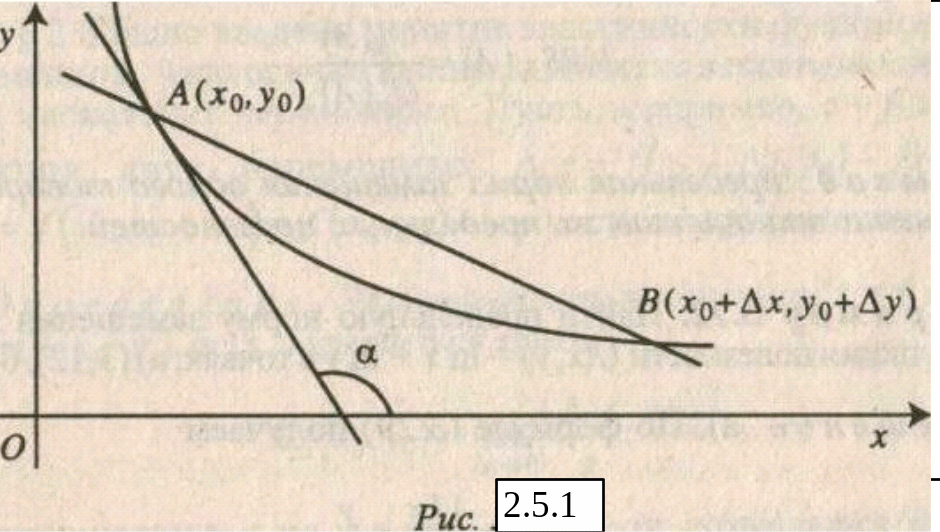
В этом случае гово­рят, что х единиц первого товара замещается на (–у) единиц второго товара (имеется в виду переход из В в А).

Предельной нормой замещения х на у в точке А называется предел отношения (–у) /х , когда точка В стремится к А, оставаясь на одной с А линии уровня функции U(x, у). Предельная норма замещения обозначается MRS_ху или MRS_ху(А), если необходимо явно указать ее зависимость от точки А.

Предельная норма замещения одного товара дру­гим равна отношению их предельных полезностей.

(2.5.3)

Пример 2.5.3. Найти предельную норму замещения х на у для функции полезности U(x,y) = ln х + ln y в точках: а) (3;12), б) (2;1).

Решение. а) По формуле (2.5.3) получаем

поэтому MRS_ху(3; 12) = 4.

б). Аналогично находим MRS_ху(2; 1) = 0,5.