Основные понятия математической статистики.

Совокупность обьектов в мат.статистике называется генеральной, если для её изучения проводится не сплошное обследование каждого обьекта совокупности, а только некоторой специальной выбранной её части.

Множество случайно отобранных из генеральной совокупность обьектов называется выборочной совокупностью или выборкой.

Обьёмом совокупности(выборочной или генеральной) называется число обьектов этой совокупности.

Репрезентативная выборка – выборка, правильно отражающая все особенности генеральной выборки. Выборка может быть повторной/бесповторной – образуется путём последовательной извлечения из генеральной совокупности нескольких членов с возвратом/без возврата каждого из них после соответвующего обследования обратно в генеральную совокупность.

Выборка считается преднамеренной, если отбор обьектов для неё из генеральной совокупности производится с определенной тенденцией, приводящей к повышению или понижению вероятности выявления изучаемого признака.

Выборка считается случайной, если все обьекты генеральной совокупности имеют равную возможность попасть в выборку.

Мгновенной(текущей) выборкой называется выборка малого обьёма, взятая из числа единиц потока продукции, изготовленных к моменту отбора в короткий промежуток времени, в котором проявление систематических погрешностей пренебрежительно мало.

Общей выборкой называется выборка, состоящая из серии мгновенных выборок.

Малой выборкой считается выборка, обьём которой меньше 25 членов. Если обьём выборки больше 25 членов, то она считается большой.

Эмпирическое распределение.

Наблюдаемые значения xi называются вариантами. Последовательность вариант, записанных в порядке возрастания с соотвествующими им частотами называют вариационным рядом.

Относительной частотой называют отношение данных частот к обьёму выборки n и обозначают wi

Таблица, устанавливающая соотвествие между значениями случайной величины и их относительными частотами, наз. Статистическим распределением случайной величины Х.

Если в декартовой системе координат отметить точку (xi,wi) (i=1,m) и соединить эти точки отрезками, то полученная ломанная линия называется полигоном относительных частот.

При большом обьёме измерения, а также если Х – непрерывная случайная величина, эмпирическое распределение частот задают в виде последоватных интервалров и соответствующих им частот наблюдения или относительных частот.

Геометрически, интервальный ряд представляется гистограммой. Гистаграммой называется ступенчатая фигура, состоящая из промоугольников, основаниями которых являются интервалы длины , а высоты равны wi/h. Площадь фигуры при этом равна 1.

Статистической или эмпирической функцией распределения случайной величины называют закон изменения относительной частоты события Х<х, в данном статистическом материале:

,

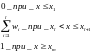Основные свойства эмпирической функции распределения: 0=<F*(х)=<1 ; F*(x) – неубывающая функция своего аргумента.

Среднее выборочное и выборочная дисперсия.

По обычным формулам ТВ только заменяя вероятность относительной частотой, вычисляют среднее значение наблюдаемой величины – среднее выборочное значение, и дисперсию наблюдаемой величины - выборочную дисперсию.

Так, среднее выборочное: , если все хi в опыте различны, а если значение хi могут быть одинаковыми, то для сгрупированных данных: , где m – число групп.

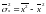Выборочная дисперсия : или более удобный вид: ; если все хi различны, или для сгрупированных данных: .

Выборочная дисперсия равна разности между средним значением квадрата случайной величины Х и квадратом её среднего значения в выборке.