Классификация дифференциальных уравнений с частными производными

В общем случае дифференциальное уравнение с частными производными 2 порядка с 2 независимыми переменными имеет вид:

Где x,y – независимые переменные, u – искомая функция, - её первые и вторые частные производные по аргументам х,y

Уравнение линейное – если оно содержит функцию и её производные только в 1ой степени.

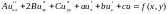
Причём коэффициенты A,B,C,a,d,c – зависят от переменных х и у или константны.

Если они константны – уравнение называется линейным с постоянными коэффициентами.

Если D - дискриминант, то при :

D > 0 – эллиптический тип

D = 0 – параболический тип

D < 0 – гиперболический тип

D не сохраняет постоянного знака – смешанный тип

С линейным диф. Уравнением всязано обыкновенное диф. Уравнение которое называют характеристическим:

Простейшее уравнение элиптического типа носит название уравнения Лапласа

Неоднородное уравнение Лапласа называется уравнением Пуассона, соответственно:

,

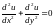Начальные и краевые условия. Задача Коши.

Диф. Уравнение с частными производными имеет в общем случае бесчисленное множество решений. Поэтому, если физический процесс описывается с помощью уравнения с частными производными, то для однозначной хар-ки этого процесса нужно к уравнению присоединить какие-то дополнительные условия. Эти дополнения состоят из начальных и краевых условий.

Различасть их можно только лишь в том случае, если в уравнении одно из независимых переменных играет роль времени, а другое – пространственно координаты. При этом условие к моменту времени – начальное, к фиксированным значениям координат – краевое.

Р-м общую постановку задачи с начальными условиями. Дано дин. Диф. Ур. . Отыскивание решения u=u(x,y) уравнения удовлетворяющего начальным условиям , называется задачей Коши, а сами условия носят название начальных данных Коши (или условий Коши) Задача Коши допускает простую геометрическую интерпретацию – требуется найти интегральную поверхность u=u(x,y) уравнения, проходящую через данную пространственную кривую и касающуюся в точке М этой кривой системы векторов а, расположенных в плоскостях х=конст.

Метод сеток. Поставка задачи.

Идея метода сеток – или иначе, метода конечных разностей, для приближенного решения краевых задач для двумерных диф. Уравнений заключается в след:

В плоской обл. G в кот. Разыскивается решение, строится сеточная обл Gh, состоящая из одинаковых ячеек и приближающая данную обл G: , где h – шаг сетки.

Контур обл Г заменим контуром Гh, проведенным по линиям сетки, как можно ближе к контуру Г. Получим область, ограниченную контуром Гh. Точки (xi,yi) называются узлами сетки. Получим 3 разных типов узлов:

Внутренние узлы, у которых 4 соседних узла принадлежат обл.G

Граничные узлы 1-го рода, кот. Принадлежат обл.G, но не явл. Внутренними

Граничные узлы 2-го рода, кот. Принадлежат обл Gh, но не принадлежал обл G

При решении:

Граничные узлы 2 рода из расчёта исключаются

В граничных узлах 1го рода значения функции принимают равным значению этой функции в ближайшей точке контура Г

Во всех внутренних узлах частные производные замениют их конечно-разностными выражениями: , .

Заданное диф. Уравнение заменяется в узлах постоенной сетки соответствующим конечно-разностным уравнением;

Составив такие ур. Для каждого из m внутренних узлов, получим систему из m уравнений, для отыскания m неизвестных значений функции во внутренних узлах сетки, т.е. будем иметь численное решение исходной задачи.

Точность зависит от выбранного шага h, но с увеличение h увеличивается кол-во узлов и сложность задачи.

Метод сеток для задачи Дирихле.