IOOD_Lab

чення клавіш Ctrl+V або Виправлення - Вставити).

15. Замініть текст комірки Е1 на «розміщення», а текст комірки G2 - на

«Число розміщень».

16.До комірки G3 введіть функцію для обчислення розміщень.

17.Вирішіть задачу, зазначену як типову в даному завданні.

Рисунок 1.13 – Вигляд електронної таблиці після введення формули і значень із приклада

18. Скопіюйте формулу на 10 комірок вниз.

Рисунок 1.14 – Вигляд електронної таблиці після копіювання формули

19

19. Перестановки. Різні впорядковані множини, які відрізняються лише порядком елементів, тобто можуть бути отримані з тої ж самої множини перес-

тановкою місцями елементів, називаються перестановками цієї множини.

Приклад типового завдання на обчислення перестановок: скільки способів іс-

нує для того, щоб розставити 5 різних книг на книжковій полиці? Важливий порядок, кількість елементів зберігається, значить - перестановка. Це окремий випадок розміщень.

20.Обчислення перестановок можна виконати з використанням тої ж функції ПЕРЕСТ(n;n). Помітьте, що обидва параметри у цієї функції в цьому випадку будуть посилатися на ту саму комірку, тому що кількість елементів зберігається.

21.В осередок I1 введіть текст «Перестановки», об'єднайте її з коміркою

J1.

22. В комірки I2 і J2 введіть текст «Кількість елементів» і «Кількість пе-

рестановок», відповідно.

23.Отформатуйте дані заголовки.

24.В комірку J3 введіть формулу для обчислення перестановок.

25.Розв’яжіть типове завдання, зазначене вище.

26.Скопіюйте формулу на 10 рядків нижче.

Рисунок 1.15 – Вигляд електронної таблиці після створення шаблона для обчислення перестановок

20

27. Самостійно з використанням цього шаблона вирішите наступні комбінаторні завдання (для обчислень можна використовувати вільні комірки,

якщо явно в умові завдання не зазначена кількість елементів множини й обира-

ної підмножини):

1. Скількома способами можуть вісім чоловік стати в чергу до театраль-

ної каси?

2.У магазині "Усе для чаю'' є 5 різних чашок і 3 різні блюдця. Скількома способами можна купити чашку із блюдцем?

3.В автомашині 7 місць. Скількома способами сім чоловік можуть сісти

вцю машину, якщо зайняти місце водія можуть тільки троє з них?

4.Скільки слів можна утворити з букв слова фрагмент, якщо слова по-

винні складатися: (а) з восьми букв, (б) із семи букв, (в) із трьох букв?

5. Скільки існує різних автомобільних номерів, які складаються з п'яти цифр, а) якщо перша з них не дорівнює нулю; б) якщо номер складається з од-

нієї букви латинського алфавіту, за котрою ідуть чотири цифри, відмінні від нуля?

6. Алфавіт деякої мови містить 30 букв. Скільки існує слів іх шести лі-

тер (ланцюжок букв від пробілу), складених з букв цього алфавіту, якщо: (а) лі-

тери в словах не повторюються? (б) букви в словах можуть повторюватися?

7. Скількома способами можна розставити на полці сім книг, якщо (а)

дві певні книги повинні завжди стояти поруч,(б) ці дві книги не повинні стояти поруч?

8.Скількома способами з восьми чоловік можна обрати комісію, що складається з п'яти членів?

9.Скількома способами можна відібрати кілька фруктів із семи яблук,

чотирьох лимонів і дев'яти апельсинів? (Ми вважаємо, що фрукти одного виду нерозрізнені.)

10. Скільки слів із 5 літер, кожне з яких складається із трьох приголос-

них і двох голосних, можна утворити з букв слова рівняння?

21

Контрольні питання

1. Яке програмне забезпечення (ПЗ) для роботи з електронними табли-

цями (ЕТ) вам відомо? Які основні функції виконує ПЗ для роботи з ЕТ?

2.Які адреси мають комірки ЕТ?

3.Яким чином можна додати формулу для обчислень в ЕТ? Де можна вводити формулу?

4.Як можна викликати попередньо встановлений список стандартних формул програми?

5.Які функції існують для обчислень максимуму й мінімуму в ЭТ?

6.Які функції існують для обчислення середнього значення в ЭТ?

7.Як здійснюється копіювання значень комірки в інші комірки?

8.Чим відрізняються абсолютна й відносна адресації комірок у форму-

лах? Привести приклади використання.

9.Як знайти суму значень яких-небудь комірок?

10.Введіть формули (математичні, НЕ електронних таблиць) для обчис-

лення сполучень, розміщень і перестановок з використанням засобу Equation у

складі пакета MS Word. Поясніть значення даних формул.

11. Наведіть приклади, у яких використовуються формули на обчислен-

ня сполучень, розміщень і перестановок.

12. Що значить «правило добутку» у комбінаториці? Приведіть прикла-

ди.

13.Дайте класичне визначення імовірності.

14.Що таке умовна імовірність?

15.Для чого застосовується формула Байеса? Приведіть приклади.

16.Для чого застосовується формула Бернуллі? Приведіть приклади.

17.Що значить «повна імовірність»? Як її розрахувати?

22

Лабораторна робота № 2

«Визначення числових характеристик випадкової величини в MS Excel»

Мета роботи: навчитися обчислювати числові характеристики випад-

кової величини.

Завдання роботи:

- вміти знаходити математичне очікування дискретної випадкової вели-

чини за допомогою Excel;

-вміти знаходити дисперсію дискретної випадкової величини;

-вміти знаходити середньоквадратичне відхилення дискретної випадко-

вої величини за допомогою Excel;

- вміти знаходити математичне очікування, дисперсію, моду, медіану,

середньоквадратичне відхилення безперервної випадкової величини.

Теоретичні відомості

Дискретною називають випадкову величину, можливі значення якої є ізольовані числа, які ця величина приймає з певними імовірностями.

Законом розподілу дискретної випадкової величини називають перелік її можливих значень і відповідних їм імовірностей. Закон розподілу дискретної

випадкової величини Х може бути заданий у вигляді таблиці, перший рядок

якої містить можливі значення хi , а друга імовірності pi :

графічно, для чого будують прямокутну систему координат, причому по осі аб-

23

сцис відкладають можливі значення хi , а по осі ординат – відповідні значення

імовірності pi . Будують крапки М1 (х1; р1 ), М 2 (х2 ; р2 ),..., М п (хп ; рп ) й з'єд-

нують їхніми відрізками прямих. Отриману фігуру називають багатокутником розподілу.

Математичним очікуванням дискретної випадкової величини Х на-

зивають суму добутків всіх її можливих значень на їхній імовірності:

n

М ( Х ) xi pi x1 p1 x2 p2 ... xn pn .

i 1

Математичне очікування служить характеристикою середнього значення випадкової величини.

Дисперсією випадкової величини Х називають математичне очікування квадрата відхилення:

D( X ) M [ X M ( X )]2 .

Обчислювати дисперсію зручно по формулі:

D( X ) M ( X 2 ) [M ( X )]2 .

Середнім квадратическим відхиленням випадкової величини Х нази-

вають квадратний корінь із дисперсії:

(X ) D(X ).

Дисперсія й середнє квадратическое відхилення служать характеристи-

ками розсіювання можливих значень випадкової величини навколо математич-

ного очікування.

Приклад. Знайти математичне очікування М (Х ) , дисперсію D( X ) й

Рішення. Математичне очікування дорівнює сумі добутків всіх можли-

вих значень Х на їхній імовірності:

М ( Х ) 2 0.3 2 0.1 3 0.2 4 0.3 7 0.1 2.1.

Для обчислення дисперсії скористаємося формулою:

D( X ) M ( X 2 ) [M ( X )]2 .

Складемо закон розподілу Х 2 :

Знайдемо шукане середнє квадратическое відхилення:

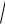(X ) D(X ) 8.69 2.948.

Початковим моментом порядку k випадкової величини Х називають

математичне очікування величини X k :

k M ( X k ) .

Зокрема, 1 M ( X ), 2 M ( X 2 ) .

Центральним моментом порядку k випадкової величини Х називають

математичне очікування величини [ X M ( X )]k :

k M [( X M ( X ))k ].

Зокрема, 1 M [ X M ( X )] 0, 2 M [( X M ( X ))2 ] D( X ) .

25

Центральні моменти доцільно обчислювати, використовуючи формули,

що виражають центральні моменти через початкові:

2 2 12 ,3 3 3 1 2 2 13.

Приклад. Дискретна випадкова величина Х задана законом розподілу:

Знайти початкові й центральні моменти першого, другого та третього порядків.

Рішення. Знайдемо початковий момент першого порядку:

1 М ( Х ) 1 0.1 2 0.3 3 0.2 4 0.3 5 0.1 3 .

Складемо закон розподілу величини Х 2 :

Знайдемо початковий момент другого порядку:

Знайдемо початковий момент третього порядку:

3 М ( Х 3 ) 1 0.1 8 0.3 27 0.2 64 0.3 125 0.1 39.6 .

Центральний момент першого порядку дорівнює нулю: 1 0 .

26

Для обчислення центральних моментів другого й третього порядків зру-

чно скористатися формулами, що виражають центральні моменти через почат-

кові:

2 2 12 10.4 32 1.4;3 3 3 1 2 2 13 39.6 3 3 10.4 2 33 0.

4. Загальний опис завдання

Лабораторна робота припускає попереднє вивчення, і засвоєння теоре-

тичних положень. У роботі напрацьовуються навички обчислення математич-

ного очікування, дисперсії, среднеквадратического відхилення випадкових величин. При рішенні завдань вивчаються різні властивості числових характе-

ристик випадкових величин.

Для безперервних випадкових величин вивчаються поняття моди й ме-

діани. При виконанні лабораторної роботи студент повинен вирішити завдання свого варіанта.

Завдання 1. Обчислення математичного очікування

Розглянемо знаходження математичного очікування для ряду дискретних значень. На рисунку 2.1 представлений ряд дискретних значень, причому в лі-

вому стовпці представлені значення, а в правом – їхньої імовірності. Матема-

тичне очікування представленого ряду значень обчислюється по наступній формулі:

=СУММПРОИЗВ(A2:A11;B2:B11).

Результат обчислень математичного очікування поміщений в комірку В13.

27

Рисунок 2.1 – Обчислення математичного очікування

Завдання 2. Обчислення дисперсії

Розглянемо приклад знаходження дисперсії випадкової величини. Знайдемо математичне очікування й зведемо його квадрат (рис. 2.2). Результат обчислень представлений осередку B13:

Рисунок 2.2 – Обчислення математичного очікування

28