
Методичка
.pdf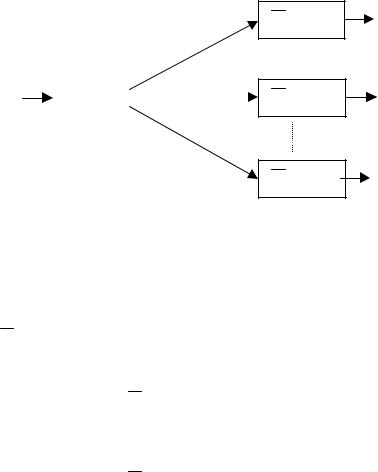
31
Si(1)
|
|
|
|
w(1) |
|
|
|
|
i |
|
|
Si-1 |
p1 |
w(2) |
W i (Si−1 ) |
p2 |
i |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
|
xi |
w(n) |
|
|
|
|
||
|
|
|
|
i |
W i+1 (Si(1))
Si(2)
W i+1 (Si(2))
Si(n)
W i+1 (Si(n))
Рис.2.10
Так как вариантов управления на i–м шаге может быть несколько, т.е. xi может принимать разные значения xi {xi(1), xi(2),K, xi(p)}, то мы выбираем то из них, при котором W i (Si−1 | xi ) становится минимальным. При этом стохастическое обобщение основного рекуррентного уравнения (2.2) имеет вид
W i (Si−1 )= min{Wi (Si−1 | xi )}
xi
или в развернутой форме
W i (Si−1 )= minx ∑(wi(j ) +Wi+1 (Si(j ))) Ρ(Si(j )
i j
| Si−1 , xi ) .
Так как мы применяем условные вероятности, то
∑Ρ(Si(j ) | Si−1 , xi )=1. j
Решение задач методом стохастического динамического программирования рассмотрим на конкретных примерах.
Пример 2.3. Решается задача управляемого перевода организма из исходного состояния S0 в конечное состояние S3 (лечение, нормализация состояния оператора). При этом существуют промежуточные состояния S1(1), S1(2), S1(3), S2(1), S2(2) , а
возможные переходы их состояния в состояние изображены на рис.2.11 в виде ориентированного ациклического графа. На ребрах графа проставлено время, требуемое для перевода организма из одного состояния в другое. В каждом состоянии Si−1 имеется несколько управляющих воздействий xi , которым соответствуют определенные наборы вероятностей перехода Ρ(Si | Si−1 , xi ). Эти

32
наборы приведены в табл.2.2-2.5. В этих таблицах, как уже отмечалось, сумма чисел в каждой строке равна 1.
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
S1(1) |
|
|
S2(1) |
|
|
|
||
|
2 |
|
6 |
|
|
|
3 |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
||||
|
4 |
|
|
|
|
|
|
||||
S0 |
|
S1(2) |
|
|
|
S3 |
|||||
|
|
|
|
|
|
|
|
||||
|
|
4 |
|
|
|
|
|||||
|
3 |
|
|
|
|
|
8 |
|
|||
|
|
|
4 |
|
|
|
|
|
|||
|
|
|
S1(3) |
|
|
|
S2(2) |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Рис.2.11 |
|
|
|
|
|||
|
|
|
|
Таблица 2.2 |
||
x1 |
|
Ρ(S1 | S0 , x1 ) |
|
|||
S1(1) |
|
S1(2) |
|
S1(3) |
|
|
|
|
|
|
|||
x(1) |
0,6 |
|
0,4 |
|
0 |
|
1 |
|
|
|
|
|
|
x(2) |
1 |
|
0 |
|
0 |
|
1 |
|
|
|
|
|
|
x1(3) |
0,3 |
|
0,3 |
|
0,4 |
|
|
|
|
Таблица 2.3 |
|
x2 |
|
Ρ(S2 | S1(1), x2 ) |
|
|
|
|
|||
|
S2(1) |
S2(2) |
|
|
x2(1) |
|
|
||
|
0,2 |
0,8 |
|
|
x2(2) |
|
0,5 |
0,5 |
|
x2(3) |
|
0,6 |
0,4 |
|
|
|
|
|
|
|
|
|
|
Таблица 2.4 |
|
|
|
|
|
Таблица 2.5 |
|
x2 |
|
Ρ(S2 | S1(2), x2 ) |
|
x2 |
|
Ρ(S2 | S1(3), x2 ) |
|
||||
|
S2(1) |
|
S2(2) |
|
|
S2(1) |
|
S2(2) |
|
||
|
|
|
|
|
|
|
|
||||
x2(4) |
|
0,5 |
|
0,5 |
|
x2(6) |
|
0,1 |
|
0,9 |
|
x2(5) |
|
0,3 |
|
0,7 |
|
x2(7) |
|
0,6 |
|
0,4 |
|
Кроме |
того, |
в состоянии S2(1) |
всегда применяется |
управление x3(1) и |
|||||||
Ρ(S3 | S2(1), x3(1))=1 , а в состоянии S2(2) всегда применяется |
x3(2) |
и Ρ(S3 | S2(2), x3(2))=1. |
|||||||||
Требуется каждому состоянию сопоставить одно оптимальное управляющее воздействие, при котором общее среднее время перехода из S0 в S3 будет минимально, а также определить это время.
Согласно рис. 2.11 и принятым нами обозначениям времена перехода организма из состояния в состояние равны

33
w = 3, |
w(1) = 2, |
w(1) |
= 2, |
31 |
23 |
1 |
|
w = 8, |
w(2) = 4, |
w(2) = 4, |
|
32 |
21 |
1 |
|
w(1) = 5, |
w(2) = 4, |
w(3) = 3 |
|
21 |
22 |
1 |
|
w22(1) = 6, |
w23(2) = 5 |
|
|
Условную оптимизацию, как и раньше, начинаем с последнего, 3-го шага управления. Из условия задачи видно, что на 3-м шаге управление вынужденное, поэтому
W 3 (S2(1))= w31 = 3, W 3 (S2(2))= w32 = 8 .
Условную оптимизацию на 2-м шаге проводим с помощью рекуррентного уравнения, которое на этом шаге приобретает вид
|
|
2 |
(S1 )= min ∑(w2(j ) + |
|
3 (S2(j ))) Ρ(S2(j ) |
W |
W |
||||
|
|
|
x2 j |
||
Допустим, что S1 |
= S1(1), тогда x2 {x2(1), x2(2), x2(3)}и |
||||
W 2 (S1(1) | x2 )= ∑2 (w21(j ) +W 3 (S2(j ))) Ρ(S2(j )
j=1
| S1 , x2 ) .
| S1(1), x2 );
W 2 (S1(1) | x2(1))= (5 +3) 0,2 +(4 +8) 0,8 =11,2 ;
W 2 (S1(1) | x2(2))= (5 +3) 0,5 + (4 +8) 0,5 =10,0 ;
W 2 (S1(1) | x2(3))= (5 +3) 0,6 + (4 +8) 0,4 = 9,6 ;
W 2 (S1(1))= min{W 2 (S1(1) | x2 )}=W 2 (S1(1) | x2(3))= 9,6 . x2
Аналогично можно найти W 2 (S1(2))=10,5 и W 2 (S1(3))= 8,2 . Далее оптимизируем 1–й шаг. Для него x1 {x1(1), x1(2), x1(3)}и
W (S0 | x1 )= ∑3 (w1(j ) +W 2 (S1(j ))) Ρ(S1(j ) | S0 , x1 );
j=1
W 1 (S0 | x1(1))= (2 +9,6) 0,6 +(4 +10,5) 0,4 =12,8 ;
W 1 (S0 | x1(2))= (2 +9,6) 1 =11,6 ;

34
W 1 (S0 | x1(3))= (2 +9,6) 0,3 + (4 +10,5) 0,3 +(3 +8,2) 0,4 =12,3 ;
W1 (S0 )= min{W1 (S0 x1 )}=W1 (S0 x1(2))=11,6 x1
Результат условной оптимизации показан на рис.2.12. В кружках проставлены значения условных минимумов Wi (Si−1 ). Из рисунка видно, что оптимальное управление на 1-м шаге равно x1(2). Оно детерминированно переводит систему в S1(1),
где наилучшее управление заключается в применении x2(3). При этом система переходит в S2(1) или в S2(2) с вероятностями, равными 0,6 и 0,4 соответственно. Если переход осуществлен в S2(1), то дальше надо применять x3(1), если же в S2(2), то оптимальное шаговое управление здесь x3(2). В обоих случаях система переходит в
S3 . Состояния S1(2) и S1(3) остаются незадействованными. Минимальное среднее время перехода из S0 в S3 составляет 11,6 единиц времени.
|
|
S(1) |
|
|
|
S(1) |
|
|
|
1 |
|
0,6 |
2 |
||
|
|
9,6 |
|
|
|
3,0 |
|
|
|
|
|
|
|
||
|
|
x(3) |
0,5 |
|
|
x(1) |
|
|
|
2 |
|
|
3 |
||
|
|
1 |
|
|
1 |
||
|
|
|
|
0,6 |
|||
S |
0 |
S(2) |
|
|
|
S3 |
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
||
11,6 |
10,5 |
|
|
|
|
|
|
x(2) |
x(4) |
|
0,4 |
||||
|
|
|
|
||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
S1(3) |
0,5 |
|
|
S2(2) |
|
|
|
8,2 |
|
|
|
8,0 |
|
|
|
|
0,4 |
|
|||
|
|
|
|
|
|
x3(2) |
|
|
|
x2(7) |
|
|
|
||
Рис. 2.12
Пример 2.4. в течение ближайших 3-х дней больному необходимо сделать срочную операцию. Для уменьшения риска неблагоприятного исхода желательно, чтобы состояние больного непосредственно перед операцией было наилучшим. С помощью медицинских обследований состояние больного оценивают по трехбалльной шкале,

35
причем оценка 1 соответствует наихудшему состоянию S1 , 2 – промежуточному S2 , 3 – наилучшему S3 . Надо рассчитать оптимальную стратегию врача (т.е. в какой из трех дней лучше всего делать операцию), если вероятности наступления состояний
S1 , S2 и S3 в любой день не зависят от состояния больного в предыдущий день и равны
p1 = P(S1 )= 0,3; p2 = P(S2 )= 0,5; p3 = P(S3 )= 0,2.
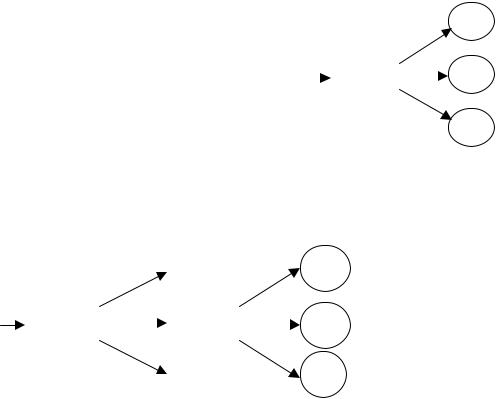
Для решения этой задачи составим дерево альтернатив, изображенное на рис.2.13.
Пусть zi - оценка состояния больного, а xi - принимаемое решение в i -й день. Тогда после измерения состояния больного в 1-й день (Изм1), еслиz1 = 3 , то x1 = Оп , т.е.
принимается решение оперировать; если z1 =1 , то x1 = Жд - ждать следующего дня, а если z1 = 2 , то возникает неопределенность (может быть принято как одно, так и другое решение). Аналогичная ситуация возникает и на второй день после процедуры Изм2, если в 1-й день принято решение Жд . Таким образом задача заключается в выработке рекомендаций о принятии оптимальных решений, если в 1-
йили во 2-й день состояние больного будет оценено как 2.
Вкачестве критерия оптимальности (целевой функции) будем использовать среднеожидаемую оценку состояния оперируемого больного, которую необходимо
максимизировать. Пусть wi(j ) - значение целевой функции на i -й день при zi= j .
Допустим, больного решили оперировать лишь на 3-й день. В этом случае среднеожидаемая оценка состояния больного перед операцией будет равна
(рис. 2.14).
w3 = w3(1) p1 + w3(2) p2 + w3(3) p3 =1 0,3 + 2 0,5 +3 0,2 =1,9 .
Этот результат показывает, что если на 2-й день мы получили z2 = 2 , то (так как это больше, чем 1,9) наилучшим будет решение x2 =< Оп > и для второго дня дерево альтернатив представляется в виде рис. 2.15. Из рисунка видно, что w2(1) = w3 .
Рассуждая аналогично, среднеожидаемая оценка состояния больного на 2-й день

36
|
|
|
|
|
<Оп> |
3 |
w1(3) |
|
|
|
<Оп> |
3 w2(3) |
|
|
|
|
<Оп> |
3 |
w3(3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
= 3 |
|
|
|
|
|
|
|
|
z3 |
= 3 |
|
|
|
|
||
|
p3 |
z1 |
= 3 |
|
|
|
|
p3 |
|
|
p3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<Оп> |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
p1 |
|
|
<Жд> |
|
|
|
p1 |
|
|
|
|
<Жд> |
|
|
|
p1 |
|
|
|
|
|
(1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Изм1 |
|
|
z |
=1 |
|
|
|
Изм2 |
|
|
|
z |
2 |
=1 |
|
|
|
|
Изм3 |
|
|
|
z |
3 |
=1 |
|
|
|
1 w3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
<Жд> |
|
|
|
|
|
|
|
|
<Жд> |
|
|
|
|
|
|
|
|
|
|
|
||||
|
p2 |
|
|
|
|
p2 |
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
z1 |
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
z2 |
= 2 |
|
|
|
|
|
|
|
|
z3 |
= 2 |
|
|
|
|
||||
|
|
|
|
|
<Оп> |
|
|
|
|
|
|
<Оп> |
|
|
|
|
|
<Оп> |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
(2) |
|
|
|
|
2 |
w2(2) |
|
|
|
|
|
|
2 |
w3(2) |
||||||||||
|
|
|
|
w1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 2.13
37
|
|
|
|
|
|
= w(1) p + w(2) p |
|
+ w(3) p |
|
=1,9 0,3 + 2 0,5 +3 0,2 = 2,17. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
w |
2 |
2 |
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
1 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Это больше, |
чем 2, |
поэтому, если в 1-й день будет |
|
|
|
|
|
|
|
|
|
|
w3(3) |
||||||||||||||||||||||||||
|
z1 = 2 ,то оптимальным решением будет воздержаться |
|
|
|
|
|
|
|
p3 |
3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
от |
операции |
в |
|
|
надежде на |
улучшение |
состояния |
|
|
|
|
|
|
|
|
p1 |
1 |
w3(1) |
|||||||||||||||||||||
больного в оставшиеся два дня, и дерево альтернатив |
|
|
|
Изм3 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
=1,9 |
|
|
|
|
||||||||||||||||||||||||||||||
для |
первого |
дня приобретает вид рис. 2.16. Из этого |
|
|
|
w3 |
|
p2 |
2 |
w3(2) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рисунка |
|
видно, |
|
|
|
что |
|
|
|
w(1) = w(2) = w |
2 |
. |
Наконец, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.14 |
|
|
|||||
среднеожидаемая оценка состояния больного в 1-й день |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
= w(1) p + w(2) |
p |
|
+ w(3) |
p |
|
= 2,17 0,3 + 2,17 0,5 +3 0,2 = 2,336 . |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
w |
2 |
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
1 |
|
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<Оп> |
3 |
|
|
|
w2(3) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
|
|
|
|
|
Z2 = 3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
<Жд> |
|
|
|
|
w(1) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Изм2 |
|
|
|
|
|
|
|
|
Z2 = 1 |
|
|
1.9 |
|
|
= |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2,17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z2 = 2 |
|
<Оп> |
2 |
|
|
|
w2(2) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 2.15
Это среднеожидаемая оценка состояния оперируемого больного, полученная за счет использования двух резервных дней. В случае, если бы эти дни не предоставлялись и больной бы оперировался всегда в 1-й день, среднеожидаемая оценка его состояния, как подсчитано выше, равнялась бы 1,9.
Таким образом, оптимальной стратегией врача будет следующая. Если в первый день состояние больного оценено на 3, то в этот день проводится операция. В случае же, если в первый день состояние больного оценивается меньше, чем на 3, решение об операции откладывается до следующего дня. Если на второй день состояние больного оценивается на 3 или на 2, то в этот день проводится операция. Если во второй день состояние больного оценено на 1, то операция откладывается на 3-й день. При такой тактике мы рассчитываем, что в момент операции состояние больного в среднем окажется равным 2,336 (вместо 1,9 при чисто случайной тактике).

38
|
|
|
|
|
|
<Оп> |
3 |
|
|
|
|
|
|
|
|
w(3) |
|
|
|
|
|
|
|
|
1 |
|
|
|
p3 |
z1 |
= 3 |
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
p1 |
|
|
<Жд> |
2,17 |
|
|
Изм1 |
z1 |
=1 |
|
|||||
|
|
|
||||||
|
|
<Жд> |
|
|||||
|
= 2,3 |
|
|
|
|
|
|
|
w1 |
|
|
|
|
w1(1) = w1(2) = |
|
||
p2 |
|
|
w2 |
|||||
|
|
z1 |
= 2 |
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 2.16
В данном примере вместо хирургической операции могут, конечно, рассматриваться и другие существенные воздействия на организм человека, успешность применения которых критична к состоянию человека, меняющемуся во времени. Можно также переформулировать эту задачу как нахождение оптимального выбора момента выполнения ответственных действия человеком (спортивных достижений; специальных заданий, выполняемых в экстремальных условиях) в ограниченном интервале времени в условиях меняющегося во времени его физиологического или психологического состояния. При этом считается, что во всех промежуточных точках заданного интервала времени состояние человека может быть оценено количественно. Задачу можно существенно усложнить, если ввести зависимость данного состояния от предыдущего.
3 ПРИМЕНЕНИЕ ТЕОРИИ ИГР ДЛЯ ОПТИМИЗАЦИИ КЛИНИЧЕСКИХ РЕШЕНИЙ В ХИРУРГИИ
3.1 Игры и методы их решения
Рассмотрим игру (модель конфликтной ситуации), в которой участвует два игрока A и B , имеющие прямо противоположные интересы, поэтому выигрыш одного равен проигрышу другого. Такая игра называется парной игрой с нулевой суммой. Если игрок A выигрывает a , то игрок B при этом выигрывает − a , поэтому сумма выигрышей всегда равна нулю. Процесс игры заключается в последовательных ходах (личных – сознательных и случайных) противников, а

39
совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от сложившейся ситуации называется стратегией игрока [6]. При конечном числе стратегий игра будет конечной. Пусть у игрока A имеется m
возможных стратегий A1, A2 ,K, Am , а у игрока B – n возможных стратегий
B1, B2 ,K, Bn . Пусть также известны величины aij – выигрыши игрока A при использовании Ai с его стороны и Bj со стороны противника. Тогда игра,
называемая игрой m ×n , может быть представлена таблицей, называемой платежной матрицей или просто матрицей игры (табл. 3.1).
Таблица 3.1
Ai B j |
B |
B |
… |
B |
|
1 |
2 |
|
n |
A1 |
a11 |
a12 |
… |
a1n |
A2 |
a21 |
a22 |
… |
a2n |
… |
… |
… |
… |
… |
Am |
am1 |
am2 |
… |
amn |
Приведение игры к матричной форме может само по себе составить трудную задачу, однако таким путем многоходовая игра фактически сводится к одноходовой
– от игрока требуется сделать только один ход: выбрать подходящую стратегию. Для данного игрока среди всех стратегий имеется оптимальная, обеспечивающая ему максимальный выигрыш. Задача теории игр – нахождение оптимальных стратегий игроков в предположении одинаковой «разумности» противников.
По матрице игры определяются нижняя α |
и верхняя β цены игры. Пусть |
||
αi = min αij , βj = max αij , тогда |
|
|
|
j |
i |
|
|
|
α = max αi = max min αij |
||
|
i |
i |
j |
|
|
||
|
β = min βj = min max αij . |
||
|
j |
j |
i |
|
|
|
|
Принцип выбора противниками стратегий, соответствующих получению ими выигрышей α и β называется принципом минимакса, а сами стратегии – минимаксными. Известно [7], что минимаксные стратегии устойчивы по отношению к информации о поведении другой стороны только в случае, если α = β. В этом случае матрица игры имеет седловую точку, а величина γ = α = β называется ценой

40
игры. Стратегии Ai и Bj , при которых достигается выигрыш γ , называются оптимальными чистыми стратегиями, а их совокупность – решением игры.
Более часто встречаются случаи, когда α ≠ β. В этом случае для получения наибольшего выигрыша игроку выгодно применять не одну (чистую) стратегию, а чередовать случайным образом несколько стратегий. Такие стратегии, состоящие в случайном чередовании чистых стратегий, называются смешанными и задаются соответствующими вероятностными векторами. Пусть SA - смешанная стратегия игрока A , а SB - смешанная стратегия игрока B . Тогда SA = (p1, p2 ,K, pm ),
SB = (q1 , q2 ,K, qn ), где pi - вероятность применения игроком A стратегии Ai , qj -
вероятность применения игроком B стратегии Bj , причем
m |
n |
∑pi = ∑qj =1. |
|
i=1 |
j =1 |
Если допустить применение смешанных стратегий (чистая стратегия – частный случай смешанной), то для каждой конечной игры можно найти хотя бы одно решение, т.е. пару устойчивых оптимальных стратегий игроков (SA* , SB* ),
обладающих следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступить от своей [6]. Выигрыш, соответствующий решению, называется, как и раньше, ценой игры и в общем случае (при применении смешанной стратегии) лежит в интервале α ≤ γ ≤ β.
|
Самая простая конечная игра – игра 2 ×2 . Ее матрица |
|
|
Таблица 3.2 |
|||||||||||||||
|
|
Ai Bj |
|
B1 |
B2 |
||||||||||||||
имеет вид табл. 3.2. Если для этой матрицы |
α = β, то игра |
|
|
|
|
|
|
|
|||||||||||
|
A1 |
|
a11 |
a12 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
имеет седловую точку и ее |
|
решение – это пара чистых |
|
A2 |
|
a21 |
a22 |
||||||||||||
стратегий, пересекающихся в седловой точке. Если же в |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
матрице |
2 ×2 седловой |
точки |
нет и α ≠ β, |
то необходимо |
искать |
|
решение |
в |
|||||||||||
смешанных |
|
стратегиях. |
Пара |
|
оптимальных |
|
смешанных стратегий |
S* = (p , p |
|
); |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
1 |
2 |
|
S* |
= (q ,q |
2 |
) |
и цена игры в этом случае определяются по формулам [7]: |
|
|
|
|
|
||||||||||
B |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 |
= |
|
|
a22 − a21 |
; |
p2 =1− p1 = |
|
a11 − a12 |
; |
(3.1) |
|
|
|
|||||
|
|
a11 |
+ a22 − a12 |
− a21 |
a11 + a22 − a12 − a21 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
