§ 6. Тензор напряжений. Интенсивность напряжений. Наибольшие касательные напряжения
Через каждую точку тела можно провести сколько угодно площадок, наклоненных ко всем трем координатным плоскостям. Из формулы (1.4) следует, что для определения напряжений на любой наклонной площадке достаточно знать напряжения на трех взаимно перпендикулярных площадках. Таким образом, девять составляющих напряжения σх, τxy, τхz, σу, τ уz, τzх, τzx τzу, σz (из них шесть попарно равны) полностью определяют напряженное состояние в точке.
На каждой координатной площадке три составляющих образуют вектор полного напряжения: на площадке с нормалью х — вектор рх, на площадке с нормалью y — рy и на площадке с нормалью z - pz. Совокупность трех векторов рх, ру и pz определяемых девятью составляющими, которые при перемене координатных осей преобразуются по формуле (1.4), называется ортогональным тензором второго ранга. Тензором первого ранга является вектор. В дальнейшем изложении сокращенно будем называть его просто тензором, а девять составляющих — компонентами тензора.
Тензор, компонентами которого являются напряжения, описывает напряженное состояние в точке и называется тензором напряжений. Он записывается в виде следующей матрицы:
(1.14)
На основании закона парности касательных напряжений компоненты тензора напряжений, расположенные симметрично относительно главной диагонали, равны между собой, поэтому тензор напряжений Тσ является симметричным.
В каждой точке упругого тела будет свой тензор напряжений, следовательно, в теле имеется поле тензоров напряжений.
Из свойств тензоров отметим два.
Тензоры можно складывать и вычитать. Суммой двух тензоров является новый тензор, компоненты которого представляют собой сумму соответствующих компонентов слагаемых тензоров.
Тензор можно умножать на скаляр. Произведением тензора на скаляр является новый тензор, компоненты которого в раз больше соответствующих компонентов умножаемого тензора.
Рассмотрим напряженное состояние, при котором на трех взаимно перпендикулярных площадках действуют только три одинаковых главных напряжения σ0, равные среднему напряжению в данной точке тела:
(1.15)
Такое напряженное состояние описывается тензором
который называется шаровым тензором напряжений.
Название «шаровой тензор» связано с предложенным Ламе геометрическим представлением напряженного состояния в точке. Если в системе координат, совпадающей с главными осями, для каждой площади, проходящей через начало координат, построить вектор полного напряжении р то концы этих векторов опишут поверхность эллипсоида, который называется эллипсоидом напряжений или эллипсоидом Ламе.
Три полуоси эллипсоида напряжений равны по длине трем главным напряжениям. В случае напряженного состояния, описываемого шаровым тензором (1.16), все три главных напряжения равны между собой и эллипсоид напряжений обращается в шар.
Используя второе из указанных свойств тензоров, шаровой тензор (1.16) можно представить в виде
Где
представляет собой так называемый единичный тензор.
Вычитая из тензора напряжений (1.14) шаровой тензор (1.16), получаем новый тензор, называемый девиатором напряжений;
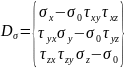
(1.19)
Таким образом, тензор напряжений в каждой точке может быть представлен в виде суммы двух тензоров: шарового тензора напряжений и девиатора напряжений (рис. 9), т. е.
Рис.9
Разложение тензора напряжений па шаровой тензор и девиатор имеет большое принципиальное значение при исследовании поведения упругих и пластических тел под нагрузкой. Шаровой тензор 0Т1 выделяет из напряженного состояния равномерное всестороннее растяжение (сжатие), при котором изменяется лишь объем данного элемента тела без изменения формы. Девиатор напряжений D0 характеризует состояние сдвига, при котором изменяется форма элемента без изменения его объема. Следовательно, девиатор напряжений указывает отклонение (девиацию) рассматриваемого напряженного состояния от всестороннего растяжения (сжатия) или отклонение приобретенной формы тела от первоначальной. Как показывают опыты, материалы по-разному реагируют на всестороннее равномерное сжатие и на напряжение сдвига
Инварианты напряженного состояния (1.12) или (1.13) можно рассматривать состоящими из компонентов тензора напряжений, поэтому их называют также инвариантами тензора напряжений.
По аналогии с инвариантами тензора напряжений построим инварианты девиатора напряжений (последние будем отмечать звездочкой). Первый инвариант девиатора напряжений
Второй инвариант девиатора напряжений
После подстановки сюда выражения среднего напряжения из формулы (1.15) и упрощения получаем
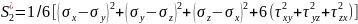
(1.21)
Второй инвариант девиатора напряжений играет существенную роль в теории пластичности, где обычно рассматривают величину, пропорциональную квадратному корню из этого инварианта, равную
(1.22)
и называемую интенсивностью касательных напряжений. Она представляет собой касательное напряжение на октаэдрнческих площадках, т. е. на площадках, равнонаклоненных ко всем трем главным напряжениям.
Вместо интенсивности касательных напряжений часто рассматривают пропорциональную ей величину
(1.23)
называемую интенсивностью напряжений, Числовой коэффициент в формуле (1.23) выбран так, чтобы при простом растяжении интенсивность напряжений была равна нормальному напряжению. Действительно, при осевом растяжении x=, y=z=xy=yz=zx=0
Подставляя эти величины в (1.23), получаем
В теории пластичности необходимо знать величину наибольших касательных напряжений. Из курса сопротивления материалов известно, что для каждой совокупности площадок, параллельных трем главным напряжениям, можно найти экстремальные значения касательных напряжений
обычно называемых главными касательными напряжениями. Одно из этих значений наибольшее:
Введем необходимое для дальнейшего изложения понятие направляющего тензора напряжений. Под ним будем подразумевать девиатор напряжений, каждый компонент которого разделен на интенсивность касательных напряжений.'
(1.26)
Направляющий тензор напряжений определяет только главные направления напряжений и соотношение между компонентами тензора напряжений, но не определяет их значения, так как компоненты направляющего тензора напряжений величины безразмерные.